1767
Rapid Free-breathing 3D SPirAl Respiratory and Cardiac Self-gated (SPARCS) Cine Acquisition Using an Undersampled Stack-of-Spirals1Department of Biomedical Engineering, University of Virginia, Charottesville, VA, United States, 2School of Artificial Intelligence, Beijing University of Posts and Telecommunications, Beijing, China, 3Department of Medicine, Stanford University, Palo Alto, CA, United States, 4Department of Medicine, University of Virginia, Charottesville, VA, United States, 5Department of Radiology, University of Virginia, Charottesville, VA, United States
Synopsis
Cardiac cine images are the gold standard techniques for analyzing cardiac function. Clinical breath-held ECG-gated Cartesian cine imaging requires 10-12 breath-holds to cover the left ventricle. Our group has developed a continuous-acquisition respiratory and cardiac self-gated cine sequence (SPARCS) for free-breathing cardiac function acquisition using 2D spiral acquisition can suffer from through-plane motion. Thus, we develop a rapid 3D self-gated cine technique using a variable density undersampled stack of spiral gradient echo sequence to provide 3D coverage of the ventricle enabling thinner slice acquisition and improved robustness to through-plane motion.
Introduction
Cardiac cine imaging is the gold standard technique for analyzing cardiac function. Clinical breath-held ECG-gated Cartesian cine imaging requires 10-12 breath-holds to cover the left ventricle. Our group has developed a continuous-acquisition respiratory and cardiac self-gated cine sequence for free-breathing cardiac function acquisition using 2D stack spiral acquisition1. To further develop the SPARCS technique, we developed a rapid 3D self-gated cine, using stack of spiral gradient echo (GRE) sequence to perform 3D cine evaluation of the left ventricle 2. To accelerate the acquisition, we used stack-of-spirals with a random variable density in the $$$k_z$$$ direction and with periodic sampling of the $$$k_z$$$=0 plane for self gating. Self-gating cardiac triggers and respiratory waveforms were derived from band-pass filtered principal component analysis (PCA) of center point of k-space over each stack of spiral volume across all the coils. Dynamic images are reconstructed by non-cartesian L1-SENSE reconstruction3,4.Methods
Acquisition StrategyOur stack-of-spiral sampling strategy consisted of a variable kz-density stack of dual density spirals rotated by the golden angle ($$$\theta = \frac{\sqrt{5}+1}{2}$$$ ). The $$$k_z$$$-t sampling scheme5 is shown on the top panel of Figure 1: Each dot corresponds to one spiral, and the color groups correspond to groups of spirals in the $$$k_z$$$ plane rotated by the golden angle between groups. We acquired 3, 5, or 7 partitions out of 10 total partitions. The first partition (shows in rectangles) of each measurement is set to $$$k_z$$$=0 and used as a self-gating navigator. Other sampled $$$k_z$$$ partition in each measurement are randomly picked from a Bates distribution6: : $$P(t,n) = -P_c+P_t\lbrace{\frac{n}{2(n-1)!}\sum\limits_{k=0}^{n}(-1)^k\tbinom{n}{k}(nt-k)^{n-1}sgn(nt-k)}\rbrace$$
where $$$P(t,n)$$$ is desired sampling partition index, $$$P_t$$$ is fully-sampled partition number, $$$P_c$$$ is central partition index, $$$n$$$ is density factor, $$$n$$$ is larger for more centralized distribution. To distribute the spirals across the partition we made sure that no $$$k_z$$$ partitions were repeated in each group, and we insured that there were equal numbers of spirals collected in each half of the $$$k_z$$$ plane.
Reconstruction
The automatic cardiac self-gating pipeline is shown in Figure 1: Self-gating cardiac signals were determined using the center point of the central partition (shown in rectangular in Sampling Scheme) of each group of spiral partitions for all receiver coils. PCA was performed to separate the cardiac and respiratory components followed by frequency spectrum analysis to extract filtered cardiac and respiratory motion signals. Figure 2 shows the retrospective cardiac binning of the data across multiple R-R intervals. Cardiac binning was performed by binning groups of undersampled 3D k-space volume (shown in colored rectangles) into one cardiac phase so that the heart could be located based on the variation in signal intensity due to cardiac motion throughout the cardiac cycle.
Non-Cartesian spiral L1-SENSE reconstruction3,4 which can be formulated as:
$$\mathop{\arg\min}\limits_{x}{\Vert{F_{u}Sx-y}\Vert}_2^2+\lambda{\Vert{\Psi{x}}\Vert}_1$$
where $$$x$$$ is the dynamic image series to be reconstructed, $$$S$$$ is the coil sensitivity maps estimated from the temporal average image using a method described by Walsh et al7, $$$F_u$$$ is the inverse Fourier gridding operator that transforms the Cartesian image space to the spiral k-space operated by gpuNUFFT8 (NVIDIA Tesla P100 GPU), $$$y$$$ is the acquired spiral k-space data, $$$\Psi$$$ is the finite time difference sparsifying bias, $$$I$$$ is the identity matrix and $$$\lambda$$$ balances between data consistency and sparsity. $$$\lambda = tTV*M_{0}$$$ was chosen as a tradeoff between image quality and temporal fidelity, where $$$M_0$$$ was the maximal magnitude value of the NUFFT image series and $$$tTV$$$ is temporal total variation factor. The objective function was solved using non-linear conjugate gradient algorithm with 24 iterations.
Imaging Experiments
6 volunteers were imaged on a 3T scanner (Skyra, Siemens Healthineers). Imaging occurred in 3 minutes after the injection of 0.075 mmol/kg of Clariscan. Stack of spiral GRE parameters are show in Table 1: FOV=320x320x80 mm3, TR=7.78ms, TE=1ms, voxel size=1.25×1.25x8mm3, flip angle=15°. A dual-density spiral-out readout trajectory was rotated by the golden angle between subsequent groups of kz measurements (containing multiple TRs) for data acquisition. The DD spiral had a fermi-function transition region with a k-space density of 0.2 times Nyquist for the first 20% of the trajectory and an ending density of 0.02 times Nyquist. Data were acquired for 80 seconds covering the left ventricle 3D volume in a double oblique orientation.
Results
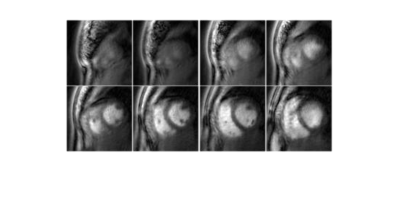
$$$tTV$$$ was optimized to reduce aliasing without causing temporal blurring. The optimal $$$tTV$$$ was 0.5 and was used for all reconstructions. Figure 3 shows reconstructed short axis end-diastole and end-systole images of sampling 3, 5 and 7 (out of 10) partitions with an 80s acquisition. Sampling 5 partitions provided a reasonable trade-off between adequately sampling the $$$k_z$$$=0 partition for self-gating while preserving a temporal resolution of 40ms. Figure 4 shows reconstructed diastolic short axis images covering the left ventricle with 5 partitions. During systole there was a reduction in contrast between the myocardium and the cavity due to the GRE readout.Discussion and Conclusion
Our proposed self-gated free-breathing 3D stack of spiral cardiac imaging strategy acquires cine images with desirable temporal and spatial resolution in short acquisition time. This strategy could provide faster and more efficient protocols for cardiac cine imaging. For future clinical study, to ensure adequate endocardial contrast during systole, we will extend our strategy to bSSFP acquisition.Acknowledgements
This work was supported by NIH R01 HL131919 and Wallace H. Coulter Foundation Grant.
References
1. Zhou R, Yang Y, Mathew RC, et al. Free-breathing cine imaging with motion-corrected reconstruction at 3T using SPiral Acquisition with Respiratory correction and Cardiac Self-gating (SPARCS). Magn Reson Med. 2019;82(2):706-720.
2. Zhang, X, Xie, G, Lu, N, et al. 3D self-gated cardiac cine imaging at 3 Tesla using stack-of-stars bSSFP with tiny golden angles and compressed sensing. Magn Reson Med. 2019; 81: 3234– 3244.
3. Otazo R, Kim D, Axel L, Sodickson DK. Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magnetic Resonance in Medicine 2010;64:767–776.
4. Feng L, Grimm R, Block KT, et al. Golden-angle radial sparse parallel MRI: Combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magnetic Resonance in Medicine 2014;72:707–717.
5. Zhao, Z, Lim, Y, Byrd, D, Narayanan, S, Nayak, KS. Improved 3D real-time MRI of speech production. Magn Reson Med. 2021; 85: 3182– 3195
6. K. Buchanan, T. Adeyemi, C. Flores-Molina, S. Wheeland and D. Overturf, "Sidelobe behavior and bandwidth characteristics of distributed antenna arrays," 2018 United States National Committee of URSI National Radio Science Meeting (USNC-URSI NRSM), 2018, pp. 1-2.
7. Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magnetic Resonance in Medicine 2000;43:682–690.
8. Knoll F, Schwarzl A, Diwoky C, Sodickson DK. gpuNUFFT – An Open Source GPU Library for 3D Regridding with Direct Matlab Interface Proc Intl Soc Magn Reson Med. 22 (2014). p 4297
Figures

Figure 1: Pipeline of cardiac self-gating. (a) Self-gating cardiac signals were determined by center one point of central partition over each stack of spiral volume for all receiver coils. (b) Principal component analysis is performed to separate the cardiac and respiratory components. (c) Frequency spectrum analysis was used to find the cardiac motion-related component. (d) Extracted filtered cardiac motion component. (e) Respiratory motion component can also be derived.
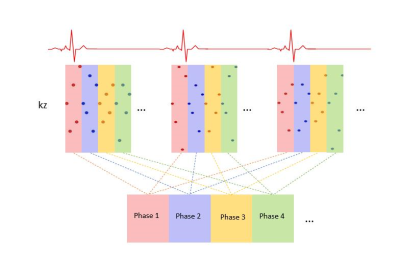
Figure 2: Retrospective cardiac binning of the data across multiple R-R intervals, was performed by binning groups of 3D k-space volume (shown in colored rectangular) into one cardiac phase so that the heart could be located based on the variation in signal intensity due to cardiac motion throughout the cardiac cycle.
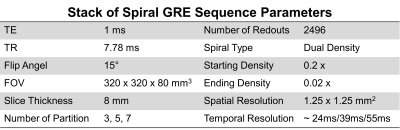
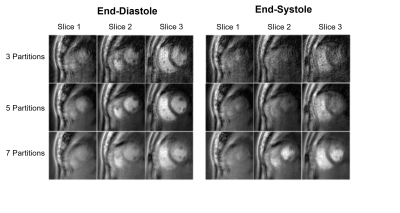
Figure 3: Reconstructed short axis end-diastole and end-systole images of sampling 3, 5 and 7 (out of 10) partitions.