1724
Sensitivity comparison of probabilistic and deterministic DTI tractography for robust characterization of arm skeletal muscle geometry1Department of Biomedical Engineering, Northwestern University, Chicago, IL, United States, 2Department of Physical Therapy and Human Movement Sciences, Northwestern University Feinberg School of Medicine, Chicago, IL, United States, 3Department of Physical Medicine and Rehabilitation, Northwestern University Feinberg School of Medicine, Chicago, IL, United States, 4Department of Neurology, Northwestern University Feinberg School of Medicine, Chicago, IL, United States
Synopsis
The robustness of probabilistic versus deterministic DTI tractography in characterization of skeletal muscle structure is not yet established. We investigated the sensitivity to turning angle when probabilistic and deterministic methods were used to estimate fascicle lengths and fractional anisotropy in the arm’s biceps muscle (n=8). Results produced with deterministic methods were highly sensitive to the turning angle, but those produced with probabilistic methods were not. Furthermore, the recommended angle in probabilistic methods yielded findings consistent with ground truth measurements, while the turning angle in deterministic methods needed to be altered from the recommended value to achieve similar results.
Introduction
Previous diffusion tensor imaging (DTI) tractography studies have investigated the difference between probabilistic tractography and deterministic tractography algorithms to produce robust results in brain applications1,2. However, for skeletal muscle applications, there have been no such sensitivity analyses for these two different tractography methods, with previous studies relying on the deterministic approach to characterize skeletal muscle fascicle geometrical properties without consideration of how a probabilistic algorithm would alter the results3. One study that applied a sensitivity analysis for one deterministic method only (using DSI Studio software) found that fascicle length estimates were highly sensitive to the turning angle parameter, but not sensitive to fractional anisotropy (FA) nor step size parameter settings4. The purpose of this study is to examine, in both probabilistic and deterministic methods, how fascicle length (FL) and fractional anisotropy (FA) estimates within the biceps arm muscle change as the turning angle varies from its default value. Previously reported cadaveric biceps measurements were used as a “ground truth” comparison for fascicle length estimates5.Methods
Image Acquisition and Pre-Processing: In 8 individuals (68.7±7.7y,1F), MR images of the dominant upper arm were acquired using a 1.5T Siemens Aera scanner with a 2x18 channel body matrix coil with arm position kept constant (Fig. 1A). T1-weighted 3D VIBE (TR=16ms,TE=7.16ms,FOV=256x304mm2,voxel=0.78x0.78x3mm3) and diffusion-weighted spin-echo EPI (TR=8500ms,TE=48ms,FOV=250x250mm2,voxel=1.25x1.25x6.5mm3) MR images were acquired. The dMR acquisition included 12 diffusion-weighted directions (b=400s/mm2) with 3 averages each, and 10 volumes with no diffusion weighting (b=0s/mm2). Fat was suppressed with Spectral Attenuated Inversion Recovery. Processing of MR data was done in the FSL software library6 (Fig. 1B). Diffusion tensors were fit at each voxel and the biceps muscle was segmented (Fig. 1C).DTI Tractography: Deterministic tractography was performed using DSI Studio7 with the turning angle varied (15°–default, 20°, 25°). Probabilistic tractography was performed using BEDPOSTX and PROBTRACKX in FSL6, with the turning angle varied (60°, 70°, 80°–default). All other tractography parameters were kept consistent between algorithms (Fig. 1C).
Post-Processing and Statistical Analysis: Coordinates of raw tracts were fitted to second-order polynomial curves, from which lengths were estimated and normalized to the humerus bone length. FA within the tract volumes were calculated. Tracts that did not meet the predetermined set of anatomical constraints (Fig. 1C) were discarded, and remaining tracts (Fig. 2) were used in further analyses. The coefficients of variance were determined for each distribution of normalized FL and FA estimates. Kruskal-Wallis one-way ANOVAs were performed to determine differences in absolute values and CoV of length and FA estimates across angles and between methods. “Best case” angles for each method were determined by choosing the angle with the most overlap between FL distribution and reported cadaveric range.
Results
Deterministic tractography showed significant differences in FL between the default angle (10°) and the two higher angles (20°,30°) (p=0.0356, p<0.001 respectively) (Fig. 3A). However, the default probabilistic tractography angle (80°) showed no differences in FL between alternate angles (60°,70°) (p=0.3096) (Fig. 3B). The default probabilistic angle (80°) estimated significantly higher FL than the default deterministic angle (10°) (p=0.0011) (Fig. 3C). Between tractography methods, was no difference between the “best case” deterministic angle (30°) and the “best case” probabilistic angle (80°) (p=0.8336) (Fig. 3D).Additionally, probabilistic methods had a higher CoV (on the same order as cadaveric CoV) of FL than deterministic methods when default angles were used (p=0.0016) (Fig. 4A), but there was no difference in CoV of FL when “best case” angles were used (p=0.3446) (Fig. 4B). Similarly, probabilistic methods had a significantly higher CoV of FA than deterministic methods when default angles were used (p=0.0274) (Fig. 4C) but were not statistically different when “best case” angles were used (p=0.5286) (Fig. 4D).
Discussion
For robust deterministic tractography to be consistent with ground truth anatomy, these results show that turning angle is critical to estimate FL, however this parameter is not sensitive for robust probabilistic tractography. Specifically, FL estimates can be optimized in deterministic tractography by changing the default turning angle, to allow for more liberal tracking and thus more anatomically accurate FL results consistent with cadaveric data. Probabilistic tractography, however, produces FL estimates within the cadaveric range across turning angles, and changing the angle does not significantly alter the results. Furthermore, increasing the turning angle in deterministic tractography results in variance of FL similar to that found in cadaveric data, while all turning angles in probabilistic tractography yield FL variances on the order of cadaveric variances.It should be noted that sensitivity to tractography parameters, as well as anatomical constraints applied, may change between muscle groups, as skeletal muscles span several different geometrical arrangements8. It is therefore important to perform a sensitivity analysis in each muscle group of interest to optimize tractography parameters and achieve the most robust structural characterization possible. This study shows that in the biceps muscle of the arm, deterministic methods are highly sensitive to the turning angle, while probabilistic methods are not.
Conclusion
Results of this study show that the default turning angle in probabilistic tractography produces robust, anatomically consistent results, but the turning angle requires sensitivity tuning from the default value in deterministic tractography to yield similar and robust results with respect to ground truth anatomy.Acknowledgements
This work was done in part with the support of NIH grants R01 HD084009, R01NS058667, R03HD094615, and a predoctoral training fellowship T32 EB025766 to DJ. We thank Marie Wasielewski for her assistance in MR imaging.
References
- Soares JM, Marques P, Alves V, Sousa N. A hitchhiker’s guide to diffusion tensor imaging. Front Neurosci 2013;7. https://doi.org/10.3389/fnins.2013.00031.
- Zhan L, Zhou J, Wang Y, Jin Y, Jahanshad N, Prasad G, et al. Comparison of nine tractography algorithms for detecting abnormal structural brain networks in Alzheimer’s disease. Front Aging Neurosci 2015;7:48. https://doi.org/10.3389/fnagi.2015.00048.
- Heemskerk AM, Damon BM. Diffusion Tensor MRI Assessment of Skeletal Muscle Architecture. Curr Med Imaging Rev 2007;3:152. https://doi.org/10.2174/157340507781386988.
- Bolsterlee B, D’souza A, Herbert RD. Reliability and robustness of muscle architecture measurements obtained using diffusion tensor imaging with anatomically constrained tractography. J Biomech 2019;86:71–8. https://doi.org/10.1016/j.jbiomech.2019.01.043.
- Murray WM, Buchanan TS, Delp SL. The isometric functional capacity of muscles that cross the elbow. J Biomech 2000;33:943–52. https://doi.org/10.1016/S0021-9290(00)00051-8.
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TEJ, Johansen-Berg H, et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 2004;23:208–19. https://doi.org/10.1016/j.neuroimage.2004.07.051.
- Yeh F-C, Verstynen TD, Wang Y, Fernández-Miranda JC, Tseng W-YI. Deterministic Diffusion Fiber Tracking Improved by Quantitative Anisotropy. PLoS One 2013;8:e80713. https://doi.org/10.1371/journal.pone.0080713.
- Wilson PD. Anatomy of Muscle. Ref Modul Biomed Sci 2014. https://doi.org/10.1016/B978-0-12-801238-3.00250-6.
Figures
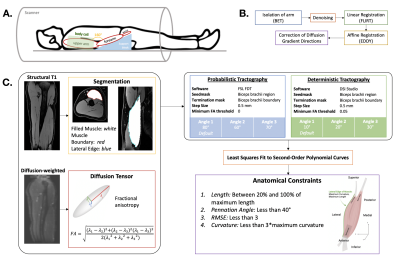
Figure 1. (A) Participant positioned in 1.5T MR scanner with 2x18 channel body coil around upper arm. (B) Steps during pre-processing of MR data, done in FSL6. (C) Workflow of MR data analysis: (i) structural T1-weighted images guided anatomical segmentations, diffusion-weighted images resulted in FA calculations; (ii) probabilistic tractography performed with stepping angles 80°, 70°, 60°, and deterministic tractography performed with stepping angles 10°, 20°, 30°; (iii) resulting tracts were fit to 2nd order polynomial curves and filtered by anatomical constraints.
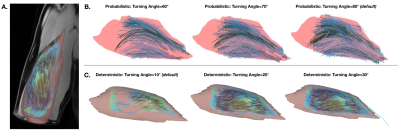
Figure 2. (A) Example of reconstructed muscle fascicles (fitted tracts that met anatomical constraints) overlaid on a segmentation of the biceps brachii muscle. (B) Examples of probabilistically tracked, anatomically constrained fascicles, at angles 60°, 70°, and 80° from left to right. (C) Examples of deterministically tracked, anatomically constrained fascicles, fascicles, at angles 10°, 20°, and 30° from left to right.
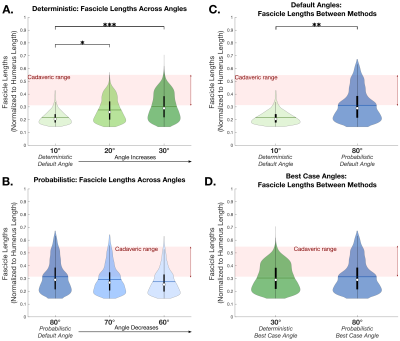
Figure 3. Fascicle lengths across three turning angles using (A) deterministic methods (left to right: 10°, 20°, and 30°) and (B) probabilistic methods (left to right: 80°, 70°, and 60°). Fascicle lengths between deterministic and probabilistic methods, using (C) default angles (deterministic: 10°, probabilistic: 80°), and (D) “best case” angles (deterministic: 30°, probabilistic: 80°). (A)-(D): Cadaveric FL range shown in red. All samples (n=8) are grouped and shown. A * indicates p<0.05, ** indicates p<0.01, and ** indicates p<0.001.
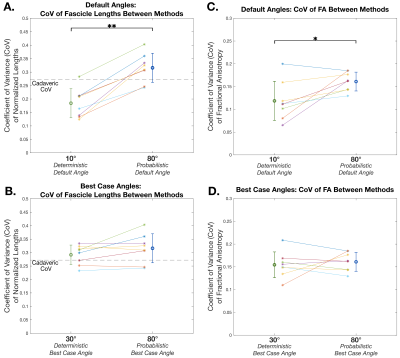
Figure 4. CoV in fascicle lengths between deterministic and probabilistic methods, using (A) default angles (deterministic: 10°, probabilistic: 80°), and (B) “best case” angles (deterministic: 30°, probabilistic: 80°). (A)-(B): Cadaveric CoV shown as dashed line. CoV in FA between deterministic and probabilistic methods, using (C) default angles (deterministic: 10°, probabilistic: 80°), and (D) “best case” angles (deterministic: 30°, probabilistic: 80°). (A)-(D): Mean±SD of subjects (n=8) are shown. A * indicates p<0.05, and ** indicates p<0.01.