1712
Tennisball: slew-efficient trajectory design for 3D-radial imaging1University of California, Berkeley, Berkeley, CA, United States
Synopsis
What is the most efficient path to traverse a sphere? For a spherical gap-minimizing efficiency definition and a particular path length, the answer happens to resemble the seam lines of a tennis ball. Here we explore properties of this general class of spherical trajectories and investigate their application to slew-constrained ZTE imaging. Static and motion-resolved imaging results demonstrate that Tennisball trajectories can achieve competitive performance with existing methods but with ~30-40% lower peak slew.
Introduction
Adjacent spokes are often spaced closely in zero echo time (ZTE) 3D-radial imaging to limit eddy-current effects, gradient-ramping time, and noise. Conventional approaches have arranged spoke endpoints along carefully spaced spherical spirals [1]. With appropriate interleaving [2], spherical spirals can achieve uniform k-space coverage over a full scan extent, but shorter time windows leave large gaps in the polar direction -- less suitable for dynamic imaging. A recent work adapts spherical spirals to better control polar versus azimuthal angular velocity [3], but increasing polar velocity in spherical spirals leads either to oversampling near the poles or greater slew variation.We consider slew-constrained 3D-radial trajectory design as an optimal path-finding problem on a sphere. Our solution resembles the seam lines of a tennis ball for a certain path length, so we call the general class of solutions "tennisball" trajectories. Here we characterize tennisball trajectory properties and report on initial results in static and motion-resolved imaging.
Theory
Consider the space of all length-$$$T$$$ continuous paths on a unit sphere $$$\mathbb{S}_2$$$. We would like to construct a path in this space that explores the sphere as efficiently as possible. We define a candidate path $$$\vec{\mathbf{k}}$$$'s inefficiency as the maximum geodesic distance between the path and any point on the sphere. We seek a solution $$$\vec{\mathbf{k}}^\star$$$ that minimizes this maximal gap:$$\vec{\mathbf{k}}^\star\in\,\operatorname{arg}\,\operatorname{min}_{||\vec{\mathbf{k}}||_2=T}\,\operatorname{max}_{\substack{\mathbf{p}\in\mathbb{S}_2}}\,d_{\mathbb{S}_2}(\vec{\mathbf{k}},\mathbf{p}).$$
This problem might be difficult to solve in general, but remarkably simple solutions exist for many values of $$$T$$$. These solutions and their constructions (Fig. 1) are inspired by recent related results in geometry [4] but are otherwise new to our knowledge. Suppose $$$T$$$ can be expressed as the sum of the circumferences of $$$L$$$ evenly spaced latitudes on the sphere, where $$$L$$$ is any positive integer. This set of latitudes achieves the minimum worst-case gap by construction (Fig. 1A). Rotating either hemisphere about any plane perpendicular to the poles does not change the maximal gap, but a continuous path emerges for certain rotation angles. Multiple rotation modes exist for $$$L>2$$$ (Fig. 1B) and offer a natural mechanism to tradeoff polar versus azimuthal velocity. We explore this property later for dynamic imaging.
Methods and Results
Tennisball implementation:We modified GE's product 3D-radial sequence to calculate and prescribe tennisball trajectories. The sequence chooses $$$L$$$ based on FOV, resolution, and slew constraint settings. Under mild slew limits, $$$L$$$ can be adjusted to balance spacing between latitudes versus spacing along the path, thereby yielding uniform coverage. Under more stringent slew limits, the sequence designs the longest path possible and operates close to the slew limit for the duration of the scan. All calculations occur at prescription time. All experiments were performed on a GE 3T MR750w scanner.
Static phantom experiment:
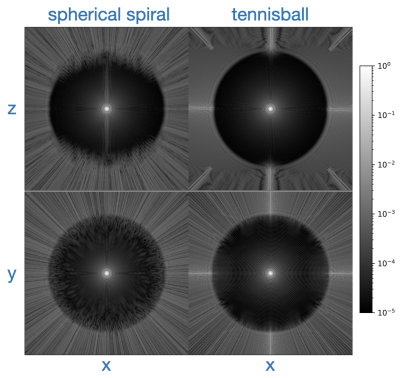
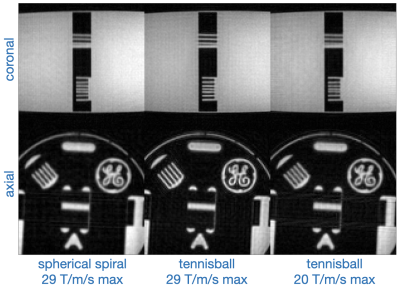
We first compared tennisball to a variation [5] of the conventional spherical spiral trajectory. All scans used 1mm isotropic resolution, 24cm FOV, 2$$$^\circ$$$ flip -- for which spherical spiral acquired 27648 spokes in 72s with 29 T/m/s peak slew. We tested two tennisball trajectories: one designed not to exceed this peak slew, and a second with a lower peak slew constraint. A rotation mode suitable for isotropic imaging (Fig. 2) was selected manually. All scans were reconstructed with BART [6]. Fig. 3 demonstrates that tennisball achieves superior image quality for the same peak slew and comparable quality at 31% lower peak slew.
Brain experiment:
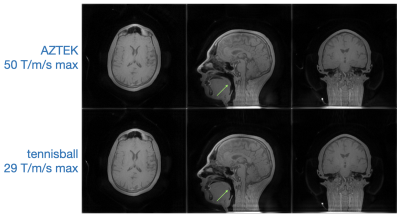
We next compared tennisball to AZTEK [3], a state-of-the-art spherical spiral trajectory that has been demonstrated for static and motion-compensated imaging. We found the publicly accessible AZTEK implementation to be largely compatible with our system, except that peak slew rates briefly and periodically exceed 400 T/m/s using recommended AZTEK parameter and product gradient amplitude settings, well in excess of hardware limits. We implemented a minimally invasive workaround by inserting intermediate spokes between large jumps as needed. The added overhead was small -- <1% when constraining to 120 T/m/s. Separate high-resolution phantom experiments showed negligible difference when constraining AZTEK slew further, so here we reduced AZTEK peak slew down to 50 T/m/s, leading to ~6% overhead in extra spokes. To compensate, we allowed AZTEK to set scan duration and adjusted tennisball parameters to meet this time limit. Tennisball and AZTEK were acquired in a healthy volunteer with a 22ch head coil. Both scans used 2mm isotropic resolution, 32cm FOV, 2$$$^\circ$$$ flip, 80896 spokes, 1m47s scan time. Figure 4 shows that tennisball achieves comparable image quality as AZTEK but with 42% lower peak slew.
Motion phantom experiment:
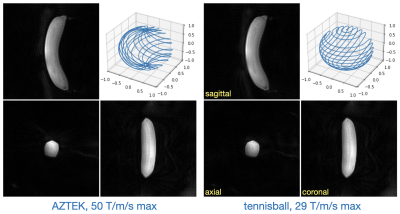
We explored setting tennisball rotation mode $$$M$$$ such that $$$L/M$$$ approximates the golden ratio, and found that that this results in small maximal gaps for short temporal windows. We adjusted $$$M$$$ accordingly and repeated the prior experiment in a motion phantom with 16ch anterior array. Fig. 5 again shows comparable performance with AZTEK but with 42% lower peak slew.
Discussion
Our results thus far demonstrate that tennisball trajectories are competitive for slew-limited 3D-radial static imaging and have potential for slew-limited imaging in the presence of motion. We suspect that golden-ratio tennisball modes and/or multi-component tennisballs (Fig. 1c) could be useful for full-scale dynamic volumetric imaging [7]. Tennisball trajectories could have relevance for other path design problems, e.g. tailoring RF pulses.Acknowledgements
We thank Shreyas Vasanawala for lending us the motion phantom, Florian Wiesinger for sharing the ZTE sequence, Marcus Alley for guidance on pulse programming, Suma Anand for assisting with experiments, and Shreya Ramachandran for assisting with early BART reconstructions. This work was supported by R01 EB009690.
References
[1] Wong ST, Roos MS. A strategy for sampling on a sphere applied to 3D selective RF pulse design. Magn Reson Med. 1994;32(6):778-784. doi:10.1002/mrm.1910320614
[2] Piccini D, Littmann A, Nielles-Vallespin S, Zenge MO. Spiral phyllotaxis: the natural way to construct a 3D radial trajectory in MRI. Magn Reson Med. 2011;66(4):1049-1056. doi:10.1002/mrm.22898
[3] Boucneau T, Fernandez B, Besson FL, et al. AZTEK: Adaptive zero TE k-space trajectories. Magn Reson Med. 2021;85(2):926-935. doi:10.1002/mrm.28483
[4] Gerlach H, von der Mosel H. On Sphere-Filling Ropes. Amer Math Monthly. 2011;118(10):863-876. doi:10.4169/amer.math.monthly.118.10.863
[5] Wiesinger F, Sacolick LI, Menini A, et al. Zero TE MR bone imaging in the head. Magn Reson Med. 2016;75(1):107-114. doi:10.1002/mrm.25545
[6] Uecker, Martin, et al. "Berkeley advanced reconstruction toolbox." Proc. Intl. Soc. Mag. Reson. Med. Vol. 23. No. 2486. 2015.
[7] Ong F, Zhu X, Cheng JY, et al. Extreme MRI: Large-scale volumetric dynamic imaging from continuous non-gated acquisitions. Magn Reson Med. 2020;84(4):1763-1780. doi:10.1002/mrm.28235
Figures
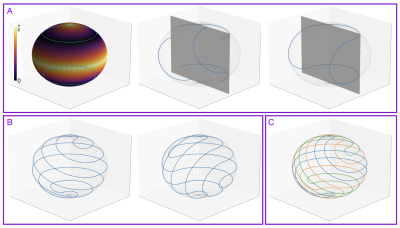
[1][A] Tennisball trajectory construction. $$$L=2$$$ latitudes are spaced evenly on a sphere (left) yielding a max geodesic distance from the latitudes of $$$\frac{\pi}{2L}$$$ (colorbar). Rotating about any plane intersecting the poles (center) yields a continuous path without changing the max geodesic distance, optimal for this path length (right). [B] For higher $$$L$$$, there are multiple modes with different polar and azimuthal velocities. [C] Variations consisting of multiple closed contours (colors) maintain good max distance for arbitrary temporal window positions.