1711

Optimal Control of the contrast in a MP-RAGE sequence: an application on the pelvis

Benoît Vernier^1,2, Eric Van Reeth^1,3, Marc Lapert², Olivier Hamelin⁴, Olivier Beuf¹, Hélène Ratiney¹, and Frank Pilleul⁴
¹CREATIS, Lyon, France, ²Siemens Healthcare SAS, Saint-Denis, France, ³CPE, Lyon, France, ⁴Centre Léon Bérard, Lyon, France

Synopsis

MRI contrast enhancement by Optimal Control is a new approach to design optimal magnetization preparation. This allows to maximize the contrast between target tissues characterized by their relaxation times. Recent numerical implementations have made possible the optimization of such preparation in a steady state sequence without full recovery between each repetition. This abstract demonstrates the contrast flexibility offered by this approach when combined with a MPRAGE sequence on pelvis imaging at 3T.

Introduction

MPRAGE¹ is a 3D sequence composed of : a magnetization preparation for contrast control; acquisition of multiple k-space lines with a short time of repetition (TR) and low flip angle spoiled gradient echo scheme; and a partial recovery step. This rapid and high spatial resolution sequence allows T1-weighted brain images thanks to an inversion recovery preparation ^2,3,4. For other clinical applications (such as for cancer imaging), other weightings could be developed. However, contrasts achievable with a preparation using both T1 and T2 relaxation times are hard to predict due to the formation of an equilibrium state. In this context, we developed an Optimal Control (OC) framework based on the GRAPE algorithm^5,6,7, that considers the full magnetization dynamics of the steady state, in order to optimize a complex preparation in this sequence.
In the present work, we investigate the possibilities offered by our method when combined with a MPRAGE to reach different contrasts between pelvis tissues on a clinical MRI scanner. Four different optimized contrasts images are acquired on a healthy volunteer to demonstrate the versatility and efficiency of the proposed sequence design.

Methode

The proposed method relies on an adaptation of the GRAPE algorithm which enables the optimization of an OC preparation composed of an arbitrary number of pulses in a MPRAGE⁷. The approach is based on the general expression of the longitudinal steady state as a function of all the parameters of the sequence (acquisition and preparation). Then, the normalized signal in the the k-space center is derived. The optimization problem is:
$$\begin{cases} \min_{u} \ C = |S_{a,i}| -|S_{b,i}|\\subject \ to\ |S_{a,i}|=0\ and\ TS =2 \end{cases} $$
Where:

Optimization variables vector composed of angles, phases and delays : $$u \in R^{\ {N\times3}+1}$$
Signal intensity of tissue a, to be saturated, or tissue b, to be maximized, after the i^th gradient echo acquisition of the readout, once the steady state is achieved : $$S_{a/b,i} $$
Time of a segment : $$TS\ (s) $$

The cost function is iteratively minimzed using gradient based approach specific to the GRAPE formalism. The cost function aims at maximizing the tissue B while saturating tissue A at k-space central line (e.g. i =1 for centric reordering). Here, preparations containing more than one pulses (2 to 5) were optimized in order to play both on T1 and T2 relaxation times.
T1 and T2 of a healthy volunteer were measured with respectively: two VIBE sequences with two different flip angles (2°,10°) and B1 correction, a CPMG train with 8 TE from 10ms to 60ms. Results were compared and harmonized with the literature⁸ (Table 1,A) .
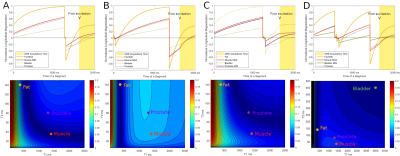
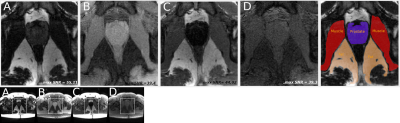
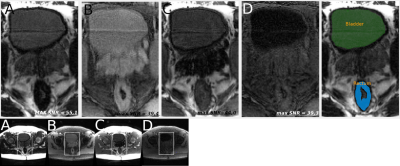
This relaxation times were used to optimize different contrasts between tissues : (A) fat enhancement with internal obturator (io) muscle saturation*, (B) io-muscle enhancement with fat saturation, (C) io-muscle enhancement with prostate saturation, (D) io-muscle enhancement with both bladder and fat saturation. (D) is more complex since two tissues were saturated.
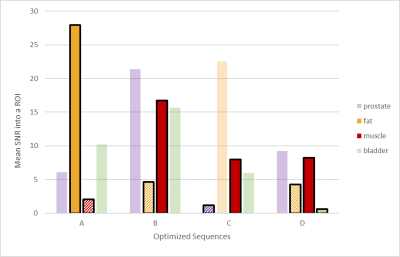
Acquistion parameters remained unchanged between the different solutions (Table 1, B). The four optimized sequences were applied on the healthy volunteer on a 3T Magnetom Vida (Siemens Healthineers, Erlangen). SNR in each region of interest was measured and compared to expected values from the theoretical model.

*Note that for the optimization A, the set of pulses angles was fixed.

Results

Optimizations resulted in the four preparation modules as below:
(A) :$$1256ms\ -\ 90^{°}\ - \ 15ms\ - 180^{°} \ - 15ms\ -\ 90_{\phi=180^{°}}^°\ -\ 330ms-\ acquisition$$
(B) :$$10ms\ -\ 90^{°}\ - \ 18ms\ - 180^{°} \ - 18ms\ -\ 90_{\phi=180^{°}}^°\ -\ 1320ms-\ 180^{°} -\ 250ms\ - acquisition$$
(C) :$$1202ms\ -\ 90^{°}\ - \ 30ms\ - 180^{°} \ - 30ms\ -\ 90_{\phi=180^{°}}^°\ -\ 354ms-\ acquisition$$
(D) :$$520ms\ -\ 90^{°}\ - \ 50ms\ - 180^{°} \ - 50ms\ -\ 90_{\phi=180^{°}}^°\ -\ 768ms-\ 180^{°} -\ 228ms\ - acquisition$$
The first line of Figure 2 shows the longitudinal magnetizations’ evolution along a cycle for all four optimized contrasts. The second line illustrates the normalized signal intensity in the center of a k-space as a function of T1/T2 values. Figure 3 and 4 confirms the good saturation of io-muscle, ischiorectal fat, prostate, ischiorectal fat and bladder respectively for optimizations (A), (B), (C) and (D) . Figure 5 shows SNR of each tissue and demonstrates that four contrasts objectives are reached.

Discussion

The results presented are a proof of concept of the proposed contrast optimization method. The OC framework can be extended to the joint optimization of preparation and detection parameters. Increasing the number of preparation pulses gives more degrees of freedom to realize more challenging contrasts or involving a higher number of tissues, such as acquisition D. It is remarkable that preparations A and C are closed to existing preparation schemes (T2Prep-IR⁹). Finally, this method allows to achieve different contrasts preserving the advantages of a given detection scheme (such as spatial resolution and coverage, motion robustness).

Conclusion

A generic optimal control framework was applied to optimize the preparation of a MP-RAGE sequence. Different contrasts are obtained on a 3T clinical MRI on the pelvis using similar acquisition parameters. Future works will investigate the benefit of this approach in the context of post-radiotherapy rectum MRI.

Acknowledgements

This work was performed within the framework of the LABEX PRIMES (ANR-11-LABX-0063) of Université de Lyon, within the program "Investissements d'Avenir" (ANR-11-IDEX-0007) operated by the French National Research Agency (ANR). version courte: ANR-11-LABX-0063

References

1. J. P. Mugler and J. R. Brookeman, “Three-dimensional magnetization-prepared rapid gradient-echo imaging (3D MP RAGE),” Magnetic Resonance in Medicine, vol. 15, no. 1, pp. 152–157, 1990, doi: 10.1002/mrm.1910150117.

2. R. Deichmann, C. D. Good, O. Josephs, J. Ashburner, and R. Turner, “Optimization of 3-D MP-RAGE Sequences for Structural Brain Imaging,” NeuroImage, vol. 12, no. 1, pp. 112–127, Jul. 2000, doi: 10.1006/nimg.2000.0601.

3. A. Sudhyadhom, I. U. Haq, K. D. Foote, M. S. Okun, and F. J. Bova, “A high resolution and high contrast MRI for differentiation of subcortical structures for DBS targeting: The Fast Gray Matter Acquisition T1 Inversion Recovery (FGATIR),” NeuroImage, vol. 47, pp. T44–T52, Aug. 2009, doi: 10.1016/j.neuroimage.2009.04.018.

4. M. Saranathan, T. Tourdias, E. Bayram, P. Ghanouni, and B. K. Rutt, “Optimization of white-matter-nulled magnetization prepared rapid gradient echo (MP-RAGE) imaging,” Magnetic Resonance in Medicine, vol. 73, no. 5, pp. 1786–1794, 2015, doi: https://doi.org/10.1002/mrm.25298.

5. N. Khaneja, T. Reiss, C. Kehlet, T. Schulte-Herbrüggen, and S. J. Glaser, “Optimal control of coupled spin dynamics: design of NMR pulse sequences by gradient ascent algorithms,” Journal of Magnetic Resonance, vol. 172, no. 2, pp. 296–305, Feb. 2005, doi: 10.1016/j.jmr.2004.11.004.

6. E. Van Reeth, H. Ratiney, M. Lapert, S. J. Glaser, and D. Sugny, “Optimal control theory for applications in Magnetic Resonance Imaging,” Pac. J. Math. Ind., vol. 9, no. 1, p. 9, Dec. 2017, doi: 10.1186/s40736-017-0034-3.

7. B. Vernier, E. Van Reeth, F. Pilleul, O. Beuf, and H. Ratiney, “MRI Contrast Enhancement of Magnetization Prepared Steady State Sequence: An Optimal Control Framework,” in 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI), Nice, France, Apr. 2021, pp. 1709–1713. doi: 10.1109/ISBI48211.2021.9434151.

8. J. Z. Bojorquez, S. Bricq et al., “What are relaxation times at 3T ?”, Magnetic Resonnance Imaging, vol. 35, pages 69-80, 2011, doi:10.1016/j.mri.2016.08.021

9. Improved delayed enhanced myocardial imaging with T2‐Prep inversion recovery magnetization preparation. J Magn Reson Imaging. 2008;28:1280–1286

Figures

Table 1: A - Relaxation times for the optimizations. B - Parameters of the sequence.

Figure 2: Upper images represent longitudinal evolution of the magnetizations over a cycle for fat, muscle, bladder and prostate. In each optimization (A, B, C, D), solid lines represent the longitudinal magnetizations of the tissues targeted in each optimization (maximized or minimized). Dotted lines represent the longitudinal magnetizations of the other tissues that are not considered in the optimization. Lower images represent transverse magnetization in the center of the k-space (i.e.after the first excitation of the acquisition time in a cycle) in the (T1/T2)-space.

Figure 3: Results of the optimized sequences on a healthy volunteer for the four different preparation modules and the same acquisition scheme. Upper images are zoomed in the prostate area. At the right, ROI segmentations used for signal intensity measurement of the internal obturator muscle (red), the prostate (purple), the fat tissue of the ischiorectal fossa (yellow).

Figure 4 : Results of the optimized sequences on our healthy volunteer for the four different preparation modules and the same acquisition. Upper images are zoomed in a plane containing the bladder and the rectum. At the right, segmentations of the bladder (green) and rectum (blue). Maximum SNR is indicated on each images.

Figure 5 : Maximaum SNR is indicated on each images. Bars surrounded by a black border represents the averaged SNR of targeted tissues in each optimization (A,B,C,D). Striped bars refer to the SNR of tissues expected to be minimized, fully colored bars refer to the signal of tissues expected to be concomitantly maximized. Semi-transparent bars represent the resulting signal of other tissues, not targeted in the optimization.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

1711

DOI: https://doi.org/10.58530/2022/1711