1705
Convex Optimized Diffusion Encoding (CODE) with Partial Fourier Imaging for EPI Diffusion Weighted Imaging1Department of Radiology, Stanford University, Stanford, CA, United States, 2Department of Bioengineering, Stanford University, Stanford, CA, United States, 3GE Healthcare, Munich, Germany, 4GE Healthcare, Boston, MA, United States
Synopsis
Diffusion weighted imaging typically uses monopolar (MONO) diffusion gradient waveforms, which may have sequence dead time that extends the TE and reduces the SNR. Partial Fourier (PF) imaging is routinely used in DWI to shorten the TE (improving SNR), but can lead to image blurring. Convex Optimized Diffusion Encoding (CODE) is a constrained optimization technique that designs time-optimal diffusion encoding gradient waveforms without sequence dead time. CODE produces a shorter TE than MONO, which leads to increased SNR. Herein, we show that CODE without PF has increased SNR and reduced image blurring compared to MONO with PF=6/8.
Introduction
Spin-Echo Echo Planar Imaging (SE-EPI) is the most widely used technique for diffusion weighed imaging (DWI) due to its acquisition speed. DWI typically uses symmetric monopolar (MONO) diffusion encoding gradient waveforms that, owing to the temporal footprint of the EPI readout, can result in sequence dead time (Fig. 1A). This timing constraint can extend the minimum achievable echo time (TE), which reduces the signal-to-noise ratio (SNR). Partial Fourier (PF) acquisitions are commonly used to acquire as little as 5/8 of the fully sampled k-space lines1. Omitted data can be synthesized using conjugate symmetry and phase corrected reconstruction approaches2-6. PF acquisitions are routinely used in DWI to shorten the TE (Fig. 1B) and limit image distortion, but can lead to Gibbs ringing7 and image blurring that can be exacerbated due to motion during the EPI readout1,8. Convex Optimized Diffusion Encoding (CODE) is a technique that poses diffusion encoding gradient waveform design as a constrained optimization problem9,10. The available gradient hardware limits and the prescribed protocol parameters are used as constraints to design time-optimal, asymmetric gradient waveforms that eliminate sequence dead time (Fig. 1C). CODE permits the use of full Fourier with a reduced TE penalty compared to MONO (Fig. 1D), which offers increased SNR. The objective of this work was to compare DWI SNR and image artifacts for MONO and CODE over a range of PF factors.Theory
The theoretical SNR for PF acquisitions can be described by Eqn. 1 as follows:$$SNR \propto e^{-TE/T_{2}} \Delta z \Delta x \Delta y \sqrt{N_{avg} \times N_{x} \times N_{y} \times PF}, \quad\quad\quad\quad \text{Eqn. [1]}$$ where T2 is the transverse relaxation time of the tissue, ∆z is the slice thickness, ∆x and ∆y are the x and y spatial resolution, Navg is the number of averages, Nx and Ny are the number of acquired k-space points, and PF is the PF factor. A protocol using ∆x=∆y=2mm, Nx=Ny=128, 2x parallel imaging, and PF=8/8 yields a TE of 73ms. Using Eqn. 1 and T2=70ms (white matter at 3T), using PF=6/8 will decrease the TE to 56ms and increase SNR by only 10%, despite the 23% reduction in TE. Depending on the imaging protocol, the SNR improvement brought about by using a PF acquisition may not always outweigh the image artifacts introduced by the PF acquisition/reconstruction.
Methods
Theoretical SNR was compared for both MONO and CODE SE-EPI DWI acquisitions using Eqn. 1 with PF acquisition factors of 5/8, 6/8, 7/8 and 8/8 (full Fourier). Phantom and brain images (n=5 healthy volunteers obtained with institutional IRB approval and consent) were acquired using a custom SE-EPI DWI pulse sequence. CODE was used to design real-time, time-optimal diffusion gradient waveforms on the scanner (i.e., gradient waveforms were not pre-computed offline). All imaging was performed using a 3T scanner (GE SIGNA Premier) with a 48-Ch Head Coil (GE Healthcare, Waukesha, WI) with the following imaging parameters: FOV=256x256mm, 2mm slice thickness with 30 slices, TR=6000ms, matrix=128x128 for phantom and brain scans, matrix=160x160 and 192x192 for phantom scans, sup> that quantifies image blur, ranging from 0 (sharp) to 1 (blurry).Results
Theoretical and measured values of SNR show that CODE has lower TEs (Table 1) and increased SNR (Fig. 2) compared to MONO, for all imaging resolutions and PF factors. At 2.0mm2 in-plane resolution, CODE allows the use of PF=8/8 with ~5% increase in SNR relative to MONO with PF=6/8 (Fig. 2A). At both 1.6mm2 in-plane resolution (Fig. 2B) and 1.3mm2 in-plane resolution (Fig. 2C), CODE allows the use of PF=8/8 with the same SNR as MONO with PF=6/8. Phantom imaging experiments at 2.0mm2 in-plane resolution also show that CODE with PF=8/8 results in higher SNR and reduced artifacts compared to MONO with PF=6/8 (Fig. 3). In vivo brain imaging experiments show qualitatively that blurring is reduced for both MONO and CODE with PF=8/8 compared to PF=5/8 (Fig. 4). Importantly, the in vivo brain images show an increase in SNR (~5%; 1.0±0.02 vs. 0.94±0.02) and reduced blurring (~10%; 0.25±0.03 vs. 0.28±0.03) for CODE with PF=8/8 compared to MONO with PF=6/8.Discussion
Theoretical SNR calculations, phantom experiments, and in vivo brain scans all show that CODE without PF offers increased SNR and reduced image blurring compared to MONO with PF=6/8. Further work is needed to explore the role of EPI-induced image distortion and to define the impact in body imaging, where susceptibility to motion could further support the use of CODE without PF. This work demonstrates that CODE without PF is a better alternative than MONO with PF for neuro DWI.Conclusion
CODE can always be used in place of MONO with or without PF acquisitions to provide shorter TEs and increased SNR. Furthermore, CODE without PF can provide an increase in SNR and a decrease in image blurring compared to MONO with PF=6/8.Acknowledgements
This project was supported, in part, by U01 EB029427 and support from GE Healthcare.References
1. Sotiropoulos SN, Jbabdi S, Xu J, Andersson JL, Moeller S, Auerbach EJ, Glasser MF, Hernandez M, Sapiro G, Jenkinson M, et al. Advances in diffusion MRI acquisition and processing in the human connectome project. Neuroimage. 2013;80:125-143.2. Noll DC, Nishimura DG, Macovski A. Homodyne detection in magnetic resonance imaging. IEEE Trans Med Imaging. 1991;10(2):154-63.
3. Bracewell RN, Bracewell RN. The Fourier transform and its applications. New York: McGraw-Hill; 1986.
4. Haacke EM, Lindskogj ED, Lin W. A fast, iterative, partial-fourier technique capable of local phase recovery. J Magn Reson. (1969) 1991;92:126-145.
5. Cuppen J, van Est A. Reducing MR imaging time by one-sided reconstruction. Magn Reson Imaging. 1987;5:526-527.
6. McGibney G, Smith MR, Nichols ST, Crawley A. Quantitative evaluation of several partial Fourier reconstruction algorithms used in MRI. Magn Reson Med. 1993;30(1):51-9.
7. Willard Gibbs J. Fourier’s series. Nature. 1898;59:200.
8. Bammer R, Holdsworth SJ, Aksoy M, Skare ST. In: Jones DK, ed. Phase Errors in Diffusion-Weighted Imaging. Diffusion MRI. Oxford University Press; 2010:218-249. Chapter 14.
9. Aliotta E, Wu HH, Ennis DB. Convex optimized diffusion encoding (CODE) gradient waveforms for minimum echo time and bulk motion–compensated diffusion‐weighted MRI. Magn Reson Med. 2017;77(2):717-29.
10. Middione MJ, Loecher M, Moulin K, Ennis DB. Optimization methods for magnetic resonance imaging gradient waveform design. NMR in Biomedicine. 2020;33(12):e4308.
11. Constantinides CD, Atalar E, McVeigh ER. Signal-to-noise measurements in magnitude images from NMR phased arrays. Magn Reson Med. 1997; 38: 852–857.
12. Do Quoc Bao (2021). Image Blur Metric. MATLAB Central File Exchange. Retrieved October 28, 2021. https://www.mathworks.com/matlabcentral/fileexchange/24676-image-blur-metric.
13. Crete F, Dolmiere T, Ladret P, Nicolas M. The blur effect: perception and estimation with a new no-reference perceptual blur metric. In Human Vis and Elect Imag XII. 2007 Feb 12 (Vol. 6492, p. 64920I). International Society for Optics and Photonics.
Figures
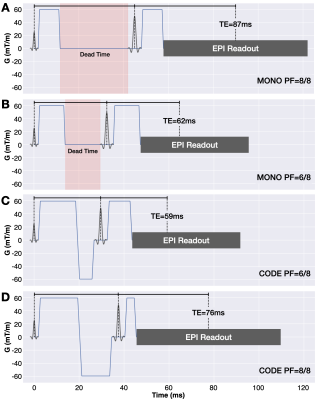
Figure 1. SE-EPI DWI pulse sequence diagrams for conventional MONO encoding with (A) PF=8/8 and (B) PF=6/8 acquisitions compared to convex optimized diffusion encoding (CODE) with PF=6/8 (C) and (D) PF=8/8. MONO has sequence dead time (shaded red regions) whereas CODE eliminates this dead time through the use time-optimal asymmetric gradient waveforms. CODE permits the use of full Fourier with a reduced TE penalty compared to MONO.
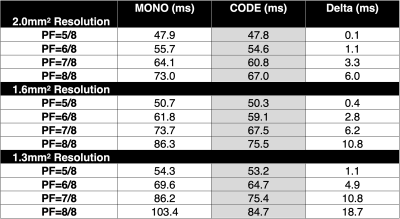
Table 1. The minimum achievable TE for MONO and CODE for 2.0mm2, 1.6mm2, and 1.3mm2 in-plane resolution as a function of the PF factor. CODE has lower TEs compared to MONO, for all imaging resolutions and PF factors. CODE permits the use of full Fourier with a reduced TE penalty compared to MONO.

Figure 2. SNR values for MONO (blue) and CODE (orange) diffusion encoding strategies as a function of the PF factor for (A) 2.0mm2, (B) 1.6mm2, and (C) 1.33mm2 in-plane resolutions. The theoretical SNR values from Eqn. 1 are indicated by solid lines while the measured SNR values from the phantom experiments are indicated by dashed lines. Theoretical and phantom SNR values are in good agreement. CODE offers a shorter TE compared to MONO, for all PF factors, resulting in consistently higher SNR.
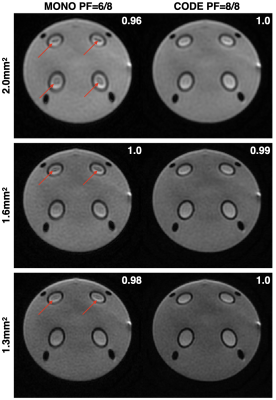
Figure 3. Phantom images acquired using MONO with PF=6/8 and CODE with PF=8/8 for spatial resolutions of 2.0mm2, 1.6mm2, and 1.3mm2 (FOV=256x256mm). Artifacts arising from PF reconstruction failures can be seen inside the four circular regions for PF=6/8 (red arrows), which are minimized when using CODE and PF=8/8. The measured normalized SNR values are listed in the top right corner of each image. CODE with PF=8/8 offers similar SNR compared to MONO with PF=6/8 without the PF artifacts.
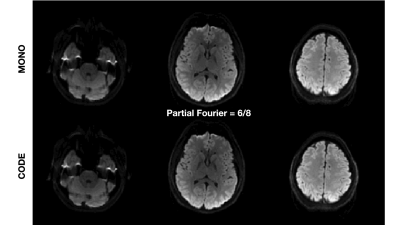
Figure 4. Example from a single volunteer showing the difference between PF=6/8 and PF=8/8 for MONO and CODE acquisitions for 2mm2 in-plane spatial resolution neuro DWI. PF=8/8 leads to reduced image blurring compared to PF=6/8 for both MONO and CODE acquisitions.