1701

Reproducibility of IVIM Quantification Across Diffusion Gradient Waveforms using Pseudo-Diffusion and Physical IVIM Signal Models

Gregory Simchick^1,2 and Diego Hernando^1,2
¹Radiology, University of Wisconsin-Madison, Madison, WI, United States, ²Medical Physics, University of Wisconsin-Madison, Madison, WI, United States

Synopsis

The intravoxel incoherent motion (IVIM) DWI signal has been shown to depend on both b-value and the first motion moment (M₁). However, traditional pseudo-diffusion IVIM signal models only include b-value dependence. In this work, monopolar and 2D (b-M₁) IVIM acquisitions were acquired using diffusion gradient waveforms with different maximum amplitudes to emulate different gradient hardware. From each acquisition, IVIM estimates were obtained by fitting pseudo-diffusion and physical (M₁ dependent) IVIM signal models. Estimated IVIM parameters were compared across acquisitions. Reproducible physical IVIM estimates were obtained using 2D IVIM-DWI acquisitions, while pseudo-diffusion IVIM estimates obtained using monopolar acquisitions demonstrated poor reproducibility.

Introduction

Intravoxel incoherent motion (IVIM) DWI has demonstrated promise in the evaluation of diffuse^1-6 and focal^1,7-11 liver diseases. However, conventional IVIM-DWI methods (using monopolar gradient waveforms) lead to high measurement variability and poor precision (repeatability and reproducibility) of IVIM perfusion fraction (F) and pseudo-diffusion (D*) measurements.^1,2,7,11-14 Recently, an IVIM-DWI acquisition utilizing 2D (b-value and first motion moment (M₁)) noise-optimized gradient waveforms was proposed, demonstrating substantially improved stability.¹⁵

Further, the perfusion component of the IVIM signal has been shown to depend on both b and M₁.^16,17 However, traditional pseudo-diffusion IVIM signal models only include b-value dependence.¹⁸ A physical IVIM signal model that includes both b and M₁ dependence has recently been proposed.¹⁶ Therefore, the purpose of this work was to evaluate the reproducibility of liver pseudo-diffusion and physical IVIM estimates obtained from 2D (b-M₁) and monopolar IVIM acquisitions.

Methods

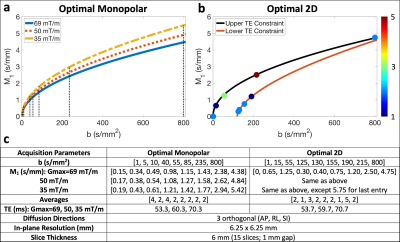
Computational methods: Cramer-Rao lower bound (CRLB) optimization was performed to determine optimal monopolar and optimal 2D (b-M₁) IVIM-DWI 20-point data samplings¹⁵ (i.e., points in the b-M₁-space that can be realized using specifically-designed diffusion gradient waveforms) based on the physical signal model¹⁶
$$S(b,M_1)=S_0[(1-F)e^{-bD}+Fe^{-bD_b}e^{-M_1^2V_b^2/2}]\qquad Eq.[1]$$
(D: diffusion coefficient, V_b: blood velocity standard deviation, D_b=1.75x10^-3 mm²/s: diffusivity of blood) and SNR=10. To emulate different MR gradient hardware, diffusion gradient waveforms were designed for each sampling three times using G_max = 35, 50, and 69 mT/m, while keeping other hardware and pulse sequence timing constraints constant.

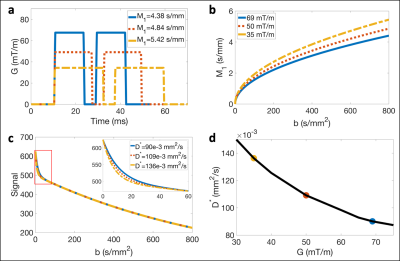
Simulations to evaluate the theoretical dependence of D* on G_max for monopolar waveforms were performed by simulating physical IVIM signals using Eq. [1] and fixed values of S₀, D, F, and V_b. Then, the simulated signals were fit to the traditional pseudo-diffusion signal model¹⁸
$$S(b)=S_0[(1-F)e^{-bD}+Fe^{-bD^*}]\qquad Eq.[2]$$
to obtain estimates of S₀, D, F, and D*.

MR acquisition: With IRB approval and informed consent, six (n=6) volunteers underwent liver MR exams (3T Signa Premier, GE Healthcare). The determined optimal monopolar and optimal 2D IVIM samplings (Figure 1a,b) were acquired using respiratory triggering and each set of waveforms described above (detailed parameters in Figure 1c).

In vivo data analysis: IVIM estimates (S₀, D, F, V_b, and D*) were obtained by performing voxelwise non-linear least squares fitting (Matlab, MathWorks) to Eqs. [1] and [2] (only monopolar datasets fit to Eq. [2]). Average measurements were determined within manually segmented ROIs covering all visible portions of the right liver lobe, excluding major vessels.

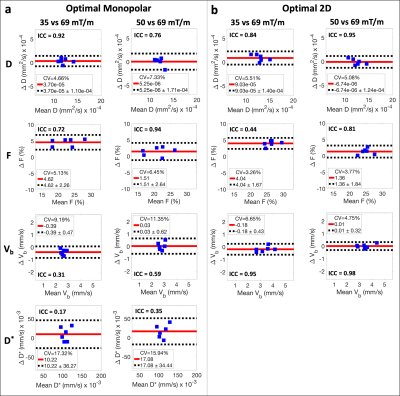
Reproducibility was evaluated by comparing measurements obtained using G_max = 35 and 50 mT/m waveforms to those using G_max = 69 mT/m (system limit). Specifically, intraclass correlation coefficients (ICCs) were calculated, and Bland-Altman analysis was performed to determine coefficients of variation (CVs), mean differences, and reproducibility coefficients (RPCs). Paired sample t-tests were also performed (significance level ⍺=0.05).

Results

Simulations illustrated that monopolar waveforms generated using different G_max follow different trajectories through the b-M₁-space (Figure 2a,b). Due to the M₁ dependence of the IVIM signal, this leads to dependence of D* estimates on G_max (i.e., poor reproducibility of monopolar-based D* measurements; Figure 2c,d).

In vivo liver experiments confirmed poor reproducibility (ICCs ≤ 0.35) of D* using monopolar waveforms with different G_max (Figure 3a). Using 2D sampling, good to excellent reproducibility (ICCs ≥ 0.81) was observed for D, F, and V_b, except for F when comparing G_max = 35 vs 69 mT/m, which demonstrated a large mean difference (4.04%; Figure 3b). Lower CVs, mean differences, and RPCs were also observed for F and V_b using 2D sampling in comparison to monopolar sampling.

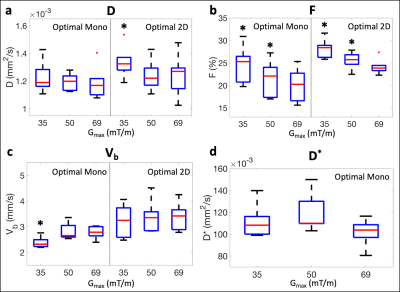
Significantly larger measurements of F were observed for G_max = 35 and 50 mT/m waveforms in comparison to the G_max = 69 mT/m waveform using both samplings (Figure 4b). Although not significant, larger measurements were also observed for D* when using monopolar waveforms with lower G_max (Figure 4d). D and F measurements were nearly identical using both signal models; therefore, only measurements using the physical signal model (Eq. [1]) are displayed in Figures 3 and 4a,b.

Discussion and Conclusion

In this work, reproducible physical IVIM estimates were obtained using 2D IVIM-DWI acquisitions with different diffusion gradient waveforms. In contrast, traditional pseudo-diffusion IVIM using different monopolar waveforms demonstrated poor reproducibility.

V_b is a fundamental physical quantity (unlike D*) that can be estimated by accounting for M₁ in the IVIM signal model. The observed reproducibility of V_b in this work suggests that V_b may be reproducible across MR gradient hardware. In this work, reproducibility was evaluated in a highly controlled manner, where G_max was varied (causing additional changes in waveform timing) while other relevant hardware features remained constant (MR system, electronics, coil, software, etc).

Although V_b demonstrated excellent reproducibility, significant differences in F were observed. These differences are likely due to confounding effects of T2 relaxation, including dependence of F (which is a signal fraction and hardware dependent) on echo time.^19,20

Limitations of this work include evaluation of reproducibility in a small number of healthy volunteers on a single MR scanner and use of a large voxel size, which may be inadequate for evaluating focal liver diseases.

In conclusion, 2D IVIM acquisitions combined with physical IVIM signal models can enable reproducible liver IVIM estimates across gradient waveforms. This work may advance the establishment of quantitative IVIM biomarkers for liver disease.

Acknowledgements

The authors acknowledge support from the NIH (R01 EB030497), from the University of Wisconsin-Madison Office of the Vice Chancellor for Research and Graduate Education with funding from the Wisconsin Alumni Research Foundation, as well as from the UW Departments of Radiology and Medical Physics. Also, GE Healthcare provides research support to the University of Wisconsin-Madison.

References

1. Li YT, Cercueil J-P, Yuan J, Chen W, Loffroy R, Wáng YXJ. Liver intravoxel incoherent motion (IVIM) magnetic resonance imaging: a comprehensive review of published data on normal values and applications for fibrosis and tumor evaluation. Quantitative imaging in medicine and surgery. 2017;7(1):59.

2. Tosun M, Onal T, Uslu H, Alparslan B, Akhan SÇ. Intravoxel incoherent motion imaging for diagnosing and staging the liver fibrosis and inflammation. Abdominal Radiology. 2020;45(1):15-23.

3. Zhang B, Liang L, Dong Y, et al. Intravoxel incoherent motion MR imaging for staging of hepatic fibrosis. PloS one. 2016;11(1):e0147789.

4. Ding L, Xiao L, Lin X, Xiong C, Lin L, Chen S. Intravoxel Incoherent Motion (IVIM) Diffusion-Weighted Imaging (DWI) in Patients with Liver Dysfunction of Chronic Viral Hepatitis: Segmental Heterogeneity and Relationship with Child-Turcotte-Pugh Class at 3 Tesla. Gastroenterology research and practice. 2018;2018.

5. Shin HJ, Yoon H, Kim M-J, et al. Liver intravoxel incoherent motion diffusion-weighted imaging for the assessment of hepatic steatosis and fibrosis in children. World journal of gastroenterology. 2018;24(27):3013.

6. Guiu B, Petit J-M, Capitan V, et al. Intravoxel incoherent motion diffusion-weighted imaging in nonalcoholic fatty liver disease: a 3.0-T MR study. Radiology. 2012;265(1):96-103.

7. Wu H, Liang Y, Jiang X, et al. Meta-analysis of intravoxel incoherent motion magnetic resonance imaging in differentiating focal lesions of the liver. Medicine. 2018;97(34).

8. Peng J, Zheng J, Yang C, et al. Intravoxel incoherent motion diffusion-weighted imaging to differentiate hepatocellular carcinoma from intrahepatic cholangiocarcinoma. Scientific Reports. 2020;10(1):1-7.

9. Zheng J, Gong XQ, Tao YY, et al. A Correlative Study Between IVIM-DWI Parameters and the Expression Levels of Ang-2 and TKT in Hepatocellular Carcinoma. Frontiers in Oncology. 2021;10:2944.

10. Kim JH, Joo I, Kim T-Y, et al. Diffusion-related MRI parameters for assessing early treatment response of liver metastases to cytotoxic therapy in colorectal cancer. American Journal of Roentgenology. 2016;207(3):W26-W32.

11. Öz A, Server S, Sökmen BK, Namal E, Inan N, Balcı NC. Intravoxel Incoherent Motion of Colon Cancer Liver Metastases for the Assessment of Response to Antiangiogenic Treatment: Results from a Pilot Study. Medical Principles and Practice. 2020;29(5):429-435.

12. Andreou A, Koh D, Collins D, et al. Measurement reproducibility of perfusion fraction and pseudodiffusion coefficient derived by intravoxel incoherent motion diffusion-weighted MR imaging in normal liver and metastases. European radiology. 2013;23(2):428-434.

13. Cui Y, Dyvorne H, Besa C, Cooper N, Taouli B. IVIM Diffusion-weighted Imaging of the Liver at 3.0 T: Comparison with 1.5 T. European journal of radiology open. 2015;2:123-128.

14. Dyvorne HA, Galea N, Nevers T, et al. Diffusion-weighted imaging of the liver with multiple b values: effect of diffusion gradient polarity and breathing acquisition on image quality and intravoxel incoherent motion parameters—a pilot study. Radiology. 2013;266(3):920-929.

15. Simchick G, Geng R, Zhang Y, Hernando D. b-M1-Optimized Waveforms for Improved Stability of Quantitative Intravoxel Incoherent Motion DWI. In Proceedings of the 29th Annual Meeting of ISMRM. 2021;Abstract 0402.

16. Ahlgren A, Knutsson L, Wirestam R, et al. Quantification of microcirculatory parameters by joint analysis of flow‐compensated and non‐flow‐compensated intravoxel incoherent motion (IVIM) data. NMR in Biomedicine. 2016;29(5):640-649.

17. Moulin K, Aliotta E, Ennis DB. Effect of flow‐encoding strength on intravoxel incoherent motion in the liver. Magnetic resonance in medicine. 2019;81(3):1521-1533.

18. Le Bihan D, Breton E, Lallemand D, Aubin M, Vignaud J, Laval-Jeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology. 1988;168(2):497-505.

19. Führes T, Riexinger AJ, Loh M, et al. Echo time dependence of biexponential and triexponential intravoxel incoherent motion parameters in the liver. Magnetic resonance in medicine. 2021.

20. Jerome NP, d’Arcy J, Feiweier T, et al. Extended T2-IVIM model for correction of TE dependence of pseudo-diffusion volume fraction in clinical diffusion-weighted magnetic resonance imaging. Physics in Medicine & Biology. 2016;61(24):N667.

Figures

Figure 1: Cramer-Rao lower bound determined optimal monopolar (a) and optimal 2D (b-M₁; b) 20-point samplings. The dashed black lines indicate the sampled b-values for the optimal monopolar sampling, and each b-M₁-pair is color coded based on the corresponding number of repetitions for the 2D sampling, which contained essentially identical b-M₁-pairs across G_max. Acquisition parameters for each sampling are given in (c). The optimal 2D sampling was constrained to have TE approximately equal to the TE of the monopolar sampling with b=800 s/mm² (space enclosed by curves in (b)).

Figure 2: Simulations illustrate non-reproducibility of D* across gradient hardware. (a) Three b=800 s/mm² monopolar diffusion gradient waveforms for different maximum gradient amplitudes (G_max). (b) Trajectories through b-M₁-space as the amplitudes of waveforms in (a) are scaled to zero. (c) Simulated IVIM-DWI signals for trajectories in (b) assuming the physical signal model (Eq. [1]) and fixed values of D, F, and V_b, as well as estimates of D* from fitting simulated signals to the traditional pseudo-diffusion signal model (Eq. [2]). (d) Simulated curve of D* as a function of G_max

Figure 3: 2D (b-M₁) IVIM sampling enables improved reproducibility of liver IVIM quantification compared to monopolar sampling. Bland-Altman plots comparing IVIM measurements obtained using different maximum gradient amplitudes (G_max). The intraclass correlation coefficient (ICC), coefficient of variation (CV), mean difference (solid red line), and mean difference ± reproducibility coefficient (RPC; dashed black lines) are displayed. Good to excellent reproducibility (ICCs ≥ 0.81) was observed for the optimal 2D sampling, except for F when comparing G_max = 35 vs 69 mT/m.

Figure 4: Boxplots of right liver lobe measurements of D (a), F (b), V_b (c), and D* (d) measured using optimal monopolar (left) and optimal 2D (right) data sampling. Significantly larger values of F were measured for waveforms with maximum gradient amplitudes (G_max) of 35 and 50 mT/m in comparison to measurements for the G_max = 69 mT/m waveform (p<0.05; denoted *). Although not significant, larger D* measurements were also observed when using waveforms with lower G_max in comparison to the G_max = 69 mT/m waveform, which is expected based on theoretical simulation results (Figure 2).

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

1701

DOI: https://doi.org/10.58530/2022/1701