1698
Fast Multi-Parametric Mapping with an Extended Spiral and Off-Resonance Readout Correction
Willem van Valenberg1, Gyula Kotek1, Mika W. Vogel2, Juan A. Hernandez-Tamames1, and Dirk H. J. Poot1
1Radiology and Nuclear Medicine, Erasmus MC, Rotterdam, Netherlands, 2GE Healthcare, Hoevelaken, Netherlands
1Radiology and Nuclear Medicine, Erasmus MC, Rotterdam, Netherlands, 2GE Healthcare, Hoevelaken, Netherlands
Synopsis
Single-shot quantitative methods with spiral sampling can increase the readout duration to reduce undersampling artifacts in the images and their propagation to the parameter maps. However, a longer readout increases blurring due to the off-resonance field if not accounted for in the reconstruction. We propose an efficient reconstruction that 1. corrects for blurring due to the off-resonance field, and 2. reduces undersampling artifacts by constraining the signal variation in each voxel to a predetermined subspace. The reconstruction method is shown to enable accurate multi-parametric mapping of a single-shot MP-b-nSSFP acquisition with submillimeter resolution in 1.8s.
Introduction
Spiral trajectories are an efficient sampling strategy for methods that estimate multiple MR parameters $$$(T_{1},T_{2},PD,ΔB_{0},B_{1}^{+})$$$ from the transient response1,2,3. Scan time and motion artifacts are minimized when the sampling is done in a single shot, but at a risk of undersampling artifacts due to reduced k-space coverage. Extending the readout duration of the spiral improves k-space coverage, but leads to image blurring, predominantly due to the off-resonance field. The blurring can be efficiently corrected during image reconstruction if the off-resonance map is known4. This correction has been shown to improve parameter estimation in MR Fingerprinting acquisitions5, but has not been applied to increase the readout length. We show that the off-resonance correction can reduce the blurring in spiral readouts of 22 ms. The correction is combined with a subspace constrained reconstruction over the images6 to enable a single-run multi-parametric acquisition with submillimeter in-plane resolution.Methods
TheoryThe effect of the off-resonance field $$$ΔB_{0}$$$ on the magnetization $$$M$$$ in voxel $$$x$$$ during the readout of point $$$p$$$ in image $$$q$$$ can be modeled as:
$$M_{p,q}(x) = e^{iΔB_0(x)t(p)}f_{q}(θ(x)) \tag{1}$$
where $$$t(p)$$$ is the timing of point $$$p$$$ relative to the start of the readout, and $$$f_{q}(θ(x))$$$ models the signal at image $$$q$$$ as function of the parameter vector $$$θ=(T_{1},T_{2},PD,ΔB_{0},B_{1}^{+})$$$. If we define $$$E_{p,q}$$$ as the linear operator that maps an image $$$M_{p,q}$$$ to the samples $$$S_{p,q}$$$ of each receive channel, we can reconstruct the images for each point $$$p$$$ and image $$$q$$$ simultaneously:
$$\hat{M}=\text{arg min}_{M} \sum_{p,q}\parallel S_{p,q}-E_{p,q}M_{p,q} \parallel_{2} \tag{2}$$
Eq. (2) is solved using an iterative method7, but is computationally complex since it requires $$$N_{p}N_q$$$ non-uniform Fourier transform. Therefore, we approximate Eq.(1) with two singular value decompositions. One to describe the phase change during the readout:
$$\left[e^{iΔB_{0}(x)t(p)}\right]_{p,x} \approx USV^H, \tag{3}$$
and the other for the contrast variations among the image:
$$\left[f_{q}(θ_i)\right]_{q,i} \approx \tilde{U}\tilde{S}\tilde{V}^H, \tag{4}$$
where $$$\left[.\right]_{q,i}$$$ constructs a matrix with $$$q$$$ and $$$i$$$ as row and column indices, $$$\left\{θ_i(x)\right\}$$$ is a set of parameter combinations sampling their expected range, and the approximations are based on respectively the first $$$N_n$$$ and $$$N_m$$$ singular vectors.
Substituting Eqs. (3) and (4) in (1), and setting $$$E_{p,q}=P_{p,q}E$$$, where $$$E$$$ is a linear operator that maps an image to all sampled k-space points, and $$$P_{p,q}$$$ select point $$$p$$$ in image $$$q$$$:
$$\hat{M}=\text{arg min}_{\tilde{M}} \sum_{p,q}\parallel S_{p,q}-\sum_{n,m}U_{p,n}S_{n,n}\tilde{U}_{q,m}P_{p,q}E \text{diag}(V_n^H) \tilde{M}_{m} \parallel_{2} \tag{5}$$
where $$$\tilde{M}_{m}\in C^{N_x}$$$ is considered unknown. Since the NUFFT only acts on the spatial dimension, we can first apply $$$E$$$ to $$$\text{diag}(V_n^H)\tilde{M}_{m}$$$, which reduces the number of NUFFTS from $$$N_pN_q$$$ to $$$N_nN_m$$$.
Experiments
The proposed method is tested using the MP-b-nSSFP acquisition3 with a 2D in-vivo scan on a 1.5T system. The pulse sequence consists of 60 pulses with $$$T_R=30$$$ ms, and the flip angles are a repeated block of four nominal rotation angles of $$$[30,175,30,175]$$$ degrees with phases of $$$[0,90,90,0]$$$ degrees. Slice thickness was 5 mm and a FOV of (250 mm)2, with 0.98 mm in-plane resolution. The proposed k-space trajectory has 6 arms, 250 kHz bandwidth, and 22 ms readout time, and a single arm is shown in Figure 1. A reference acquisition is done using 32 arms, 250 kHz bandwidth, and 4 ms readout time. The $$$ΔB_0$$$ and $$$B_1^-$$$ maps used in the reconstruction are determined from a MGE acquisition. The MP-b-nSSFP series are reconstructed with and without off-resonance compensation, and using both the full data matrix and a retrospective undersampling of the data to a single arm per image. Parameters are estimated through the least-squares fitting of a single-spin signal model.
Results
The SVDs had $$$N_n=10$$$ and $$$N_m=21$$$ components that each represented 99.9% of the energy.Figure 2 shows the first image of the fully sampled acquisition with 6 arms, with and without off-resonance compensation. The off-resonance compensation reduces blurring indicated by the sharper transition between gray and white matter.
Figure 3 shows the parameters maps of the single-shot acquisition and the fully-sampled reference. The maps of the single-shot acquisition show a higher noise presence, but accurate $$$T_1$$$ and $$$T_2$$$ values.
Discussion and conclusion
The off-resonance correction reduced the blurring in long spiral readout, but increases the reconstruction time approximately by a factor $$$N_n$$$. The $$$T_2^*$$$ relaxation also becomes more relevant with longer readouts, but doesn’t seem problematic in this case. The $$$ΔB_0$$$ and $$$B_1^-$$$ maps used for the reconstruction are currently estimated from a separate MGE acquisition, but the MP-b-nSSFP sequence properly recovers these as well and we expect that this could be used in the reconstruction process. The noise in the parameter maps from the single shot acquisition can likely be reduced by including regularization in the reconstruction. The combination of off-resonance correction and subspace-constraint in the reconstruction enabled accurate parameter maps with 0.98 mm resolution with a 1.8s acquisition for a single slice.Acknowledgements
This work was supported partially by GE Healthcare (Work statements: B-GEHC-8-2018 and B-GEHC-10_SETI II).References
- Ma D, Gulani V, Seiberlich N, et al. Magnetic resonance fingerprinting. Nature 2013;495:187–192 doi: 10.1038/nature11971.
- Gómez PA, Cencini M, Golbabaee M, et al. Rapid three-dimensional multiparametric MRI with quantitative transient-state imaging. Scientific Reports 2020;10:13769 doi: 10.1038/s41598-020-70789-2.
- Kotek G, Nunez-Gonzalez L, Vogel MW, Krestin GP, Poot DHJ, Hernandez-Tamames JA. From signal-based to comprehensive magnetic resonance imaging. Sci Rep 2021;11:17216 doi: 10.1038/s41598-021-96791-w.
- Man L-C, Pauly JM, Macovski A. Multifrequency interpolation for fast off-resonance correction. Magnetic Resonance in Medicine 1997;37:785–792 doi: 10.1002/mrm.1910370523.
- Ostenson J, Robison RK, Zwart NR, Welch EB. Multi-frequency interpolation in spiral magnetic resonance fingerprinting for correction of off-resonance blurring. Magnetic Resonance Imaging 2017;41:63–72 doi: 10.1016/j.mri.2017.07.004.
- Tamir JI, Ong F, Anand S, Karasan E, Wang K, Lustig M. Computational MRI With Physics-Based Constraints: Application to Multicontrast and Quantitative Imaging. IEEE Signal Processing Magazine 2020;37:94–104 doi: 10.1109/MSP.2019.2940062.
- Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magnetic Resonance in Medicine 2001;46:638–651 doi: 10.1002/mrm.1241.
Figures
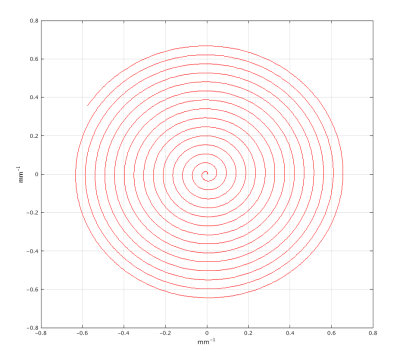
Figure 1: Spiral arm with 22 ms readout
duration, as used in the single-shot acquisition.
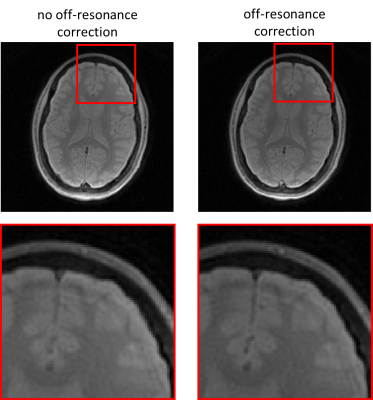
Figure 2: Off-resonance correction reduces
blurring in the first image of the MP-b-nSSFP pulse sequence, with full
sampling.
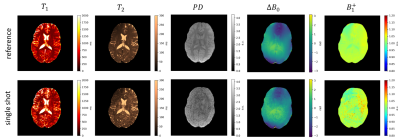
Figure 3: Parameter maps from the fully
sampled reference (top) and the single-shot (bottom) acquisition with B0 correction.
DOI: https://doi.org/10.58530/2022/1698