1697
A Beamforming-Based Coil Combination Method to Reduce Streaking Artifacts and Preserve Phase Fidelity in Radial MRI1Department of Radiological Sciences, University of California Los Angeles, Los Angeles, CA, United States, 2Department of Bioengineering, University of California Los Angeles, Los Angeles, CA, United States
Synopsis
Radial acquisition can be sensitive to hardware imperfections such as gradient non-linearity and B0 field inhomogeneity. This usually becomes accentuated in areas more distant to the isocenter and can lead to streaking artifacts even when nominally fulfilling Nyquist criteria. Previous work demonstrated beamforming-based methods for radial streaking reduction, but did not explicitly consider phase and did not evaluate the artifact-suppression performance on phase explicitly. In this work, we developed a new beamforming formulation based on minimum-variance distortionless response (MVDR) that can suppress streaking artifact while preserving accurate phase information
Introduction
Radial acquisition has been increasingly used in free-breathing abdominal MRI applications1,2 due to its inherent motion robustness. However, radial acquisition can be sensitive to hardware imperfections3,4 such as gradient non-linearity and B0 field inhomogeneity. This usually becomes accentuated in areas more distant to the isocenter (e.g., arms in abdominal scans) and can lead to streaking artifacts even when nominally fulfilling Nyquist criteria. Different approaches have been proposed to suppress the streaking artifacts resulting from these sources, including (1) a coil selection-based method5 that automatically chooses coils with less artifacts and (2) a beamforming-based method6 that combine coils with specific weights to suppress streaking artifacts. Previous work demonstrated beamforming-based methods can provide better radial streaking reduction6. However, previous beamforming-based methods did not explicitly consider phase, which is important for applications including fat quantification1, temperature mapping7, and quantitative susceptibility mapping8. In this work, we developed a new beamforming formulation that can suppress streaking artifact while preserving accurate phase information.Theory
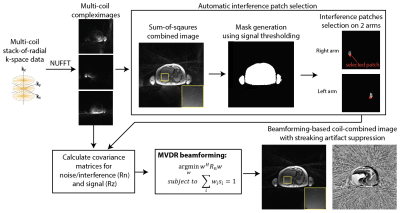
We assume the received signal in ith coil is $$$y_i=s_ix+n_i$$$, where $$$x$$$ represents the underlying magnetization, $$$s_i$$$ represents ith coil sensitivities and $$$n_i$$$ represents the noise and interference in the i-th coil. We use “interference” to refer to streaking artifacts resulting from hardware imperfection. A previous beamforming-based method6 aimed to find coil combination weights $$$w_i$$$ such that the combined image $$$m=\sum_iw_iy_i+w_in_i$$$ has maximized signal-to-noise ratio (SNR). An optimization problem is formulated in each pixel or patch: $$$argmax_w\frac{E(w^H(s_ix))}{E(w^Hn)}=\frac{w^HR_zw}{w^HR_nw}$$$, where $$$E(.)$$$ represents expectation operator, $$$R_z$$$ and $$$R_n$$$ represent covariance matrices of received signal $$$sx$$$ and noise/interference $$$n$$$ which can be estimated from the multi-coil images. In previous work6, the solution of $$$w$$$ is $$$F(\hat{R}_n^{-1} \hat(R_z))$$$, where $$$F(.)$$$ extracts the dominant eigenvector. The potential problem in this max-SNR formulation is that phase information is not explicitly considered. Any weight $$$we^{j\phi}$$$ with an arbitrary phase offset $$$\phi$$$ is also an optimal solution. The resulting phase will be dependent on the numerical algorithm used to solve the eigenvalue problem. While it may not affect applications that only consider magnitude images, it may contribute to errors when phase is of interest.In this work, we present a new formulation that is based on minimum-variance distortionless response (MVDR) beamformer in antenna theory9. We propose to find weights w by solving the optimization problem: $$$argmin_w w^HR_nw $$$ subject to $$$ \sum_iw_is_i=1$$$. The constraint $$$\sum_iw_is_i=1$$$ corresponds to “distortionless response” which will preserve the signal from the specific direction in a complex domain. The analytic solution to this MVDR problem is $$$\frac{\hat(R)_n^{-1}s}{s^H\hat(R)_n^{-1}s}$$$. While s is typically unknown, it can be estimated by extracting the principal component from local patches.
Methods
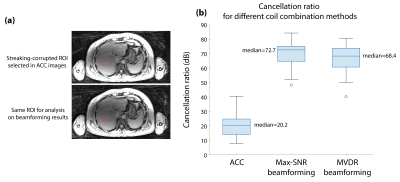
We evaluated our proposed MVDR algorithm using data from 30 free-breathing abdominal scans at 3T (MAGNETOM Prisma and Skyra, Siemens Healthineers, Erlangen, Germany). We used a 3D multi-echo stack-of-radial gradient echo sequence. The following scan parameters were used: TEs = [1.23, 2.46, 3.69, 4.92, 6.15, 7.38] ms, TR = 8.85ms, flip angle = 5°, field-of-view (FoV) = 300x300 to 460x460 mm2, slice thickness = 5mm.We compared 3 different coil combination algorithms: (1) adaptive coil combine (ACC)10, (2) Max-SNR beamforming6, and (3) proposed MVDR beamforming. Beamforming-based methods require identification of interference source (e.g., arms in abdominal scans). As discussed in previous work and in our experiences, in the case of hardware imperfections, arms at the periphery could be distorted and shrink which result in high intensities in small regions. Therefore, we used an automated heuristic approach to identify the interference source (Figure 1). The image was first segmented into 3 separate regions (body and two arms) and “interference patches” in the arm with maximal intensities were extracted. Covariance matrices of the interference were then calculated. All 3 approaches required estimation of local signal covariance matrices. Different patch sizes (5x5, 11x11 and 17x17) were compared for local patch extraction.
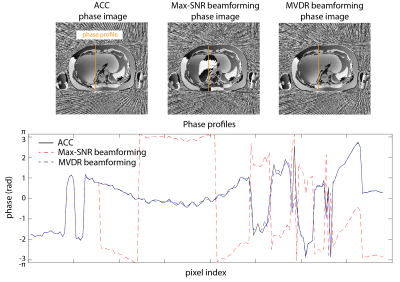
To assess the performance of streaking reduction, we used a metric known as cancellation ratio11 =$$$\frac{w_q^HR_nw_q}{w^HR_nw}$$$, where $$$w_q$$$ is a quiescent vector, $$$w$$$ is the calculated coil combination weights, and is the covariance matrix for interference. We also compared phase consistency along cross-section lines on phase images.
Results
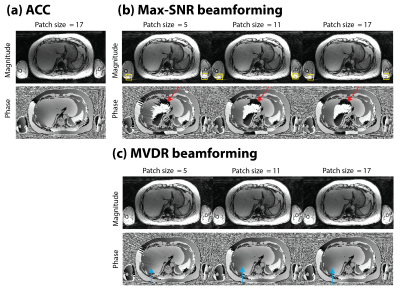
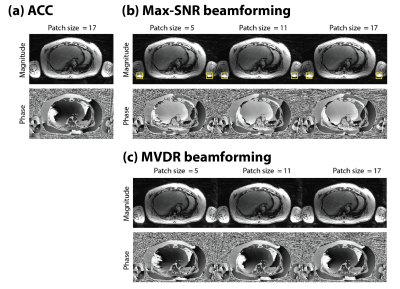
Figures 2-3 compare the magnitude and phase of the first-echo coil-combined images using different methods. Max-SNR beamforming resulted in phase jumps that do not come from phase wraps (red arrows). Small patch size of 5x5 for calculation of signal covariance matrices can be sufficient for artifact suppression in magnitude images. However, larger patch size is required for suppressing streaking artifacts in phase images. Figure 4 shows that max-SNR beamforming could create phase jumps. Figure 5 compares cancellation ratio for these 3 methods.Discussion
Compared with previous works that only investigated beamforming-based streaking reduction in magnitude images, we investigate beamforming on both magnitude and phase images and propose a new MVDR formulation that preserves consistent phase information. Although the performance of interference suppression decreased a little for MVDR beamformer compared with max-SNR beamformer in terms of cancellation ratio, MVDR provides consistent phase information that is important in phase-sensitive applications.Conclusion
We propose a new beamforming coil combination method based on minimum-variance distortionless response beamformer formulation that can suppress the streaking artifacts from hardware imperfection and preserve consistent phase information in radial MRI.Acknowledgements
The authors thank Dr. Tess Armstrong and MRI technologists at UCLA for data collection, and thank Dr. Xiaodong Zhong at Siemens for technical support. This project was supported by the UCLA Radiological Sciences Exploratory Research Program and the National Institute of Diabetes and Digestive and Kidney Diseases (R01DK124417).References
1. Armstrong T, Dregely I, Stemmer A, Han F, Natsuaki Y, Sung K, Wu HH. Free‐breathing liver fat quantification using a multiecho 3 D stack‐of‐radial technique. Magnetic resonance in medicine 2018;79(1):370-382.
2. Li Z, Fu Z, Keerthivasan M, Bilgin A, Johnson K, Galons J-P, Vedantham S, Martin DR, Altbach MI. Rapid high-resolution volumetric T1 mapping using a highly accelerated stack-of-stars Look Locker technique. Magnetic Resonance Imaging 2021;79:28-37.
3. Du J, Thornton F, Fain S, Korosec F, Browning F, Grist T, Mistretta C. Artifact reduction in undersampled projection reconstruction MRI of the peripheral vessels using selective excitation. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 2004;51(5):1071-1076.
4. Moussavi A, Untenberger M, Uecker M, Frahm J. Correction of gradient‐induced phase errors in radial MRI. Magnetic resonance in medicine 2014;71(1):308-312.
5. Xue Y, Yu J, Kang HS, Englander S, Rosen MA, Song HK. Automatic coil selection for streak artifact reduction in radial MRI. Magnetic resonance in medicine 2012;67(2):470-476.
6. Mandava S, Keerthivasan MB, Martin DR, Altbach MI, Bilgin A. Radial streak artifact reduction using phased array beamforming. Magnetic resonance in medicine 2019;81(6):3915-3923.
7. Zhang L, Armstrong T, Li X, Wu HH. A variable flip angle golden‐angle‐ordered 3D stack‐of‐radial MRI technique for simultaneous proton resonant frequency shift and T1‐based thermometry. Magnetic resonance in medicine 2019;82(6):2062-2076.
8. Jerban S, Lu X, Jang H, Ma Y, Namiranian B, Le N, Li Y, Chang EY, Du J. Significant correlations between human cortical bone mineral density and quantitative susceptibility mapping (QSM) obtained with 3D Cones ultrashort echo time magnetic resonance imaging (UTE-MRI). Magnetic resonance imaging 2019;62:104-110.
9. Van Trees HL. Optimum array processing: Part IV of detection, estimation, and modulation theory: John Wiley & Sons; 2004.
10. Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 2000;43(5):682-690.
11. Haimovich AM, Bar-Ness Y. An eigenanalysis interference canceler. IEEE Transactions on signal processing 1991;39(1):76-84.
Figures