Introduction

Field monitoring (FM) has shown great utility for correcting field perturbations up to third order in space from effects including eddy currents, heating, and mechanical vibrations¹. This is performed by monitoring the spatiotemporal field evolution, which can be described as²:
$$\boldsymbol{k}(t) = \boldsymbol{P}^{+}\boldsymbol{\phi}_{P}(t))\tag{1}$$
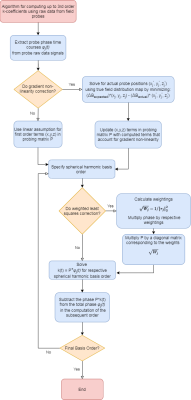
where φ_P(t) is the extracted probe phase, P⁺ is a pseudoinverse probing matrix of spherical harmonic basis functions that characterize the phase, and k(t) which are the spherical harmonic basis coefficients (k-coefficients) that describe the spatiotemporal field evolution. FM can be performed sequentially, where field cameras characterize field dynamics in an empty scanner, and the measurements are used to correct images from a subsequent identical acquisition³. Concurrent FM is performed simultaneous to patient scanning, and unlike sequential FM, patient-induced perturbations are tracked, while also improving user workflow⁴. This is made possible by integrating field probes into a radiofrequency (RF) coil. Depending on coil design and spatial constraints, the field probes may require placement in the non-linear region of the gradient coil. Occupying this region can have adverse effects on probe magnitudes and decay lifetimes. As a result, higher order fits become erroneous, and images reconstructed with unreliable k-coefficients degrade image quality. We propose an algorithm that aims to improve the integrity of FM data acquired with concurrent FM. Correction A accounts for gradient non-linearity (GNL) by correcting probe positions and first-order terms that are inputted into P⁺. This was made possible by mapping the gradient field distribution inside the scanner via a spherical-harmonic expansion, coupled with vendor-provided coefficients⁵. Secondly, k(t) is solved one order at a time instead of simultaneously to avoid inaccurate fitting from simultaneous fitting of all terms (Correction B). Lastly, to further penalize probes that are farther in the non-linear region, weighted least squares is performed using the following weighting scheme (Correction C):
$$W_j = 1/\left\|r_j\right\|_2^4\tag{2}$$
where W is a matrix of probe weights and inversely depends on the Euclidean distance of probes from isocentre. In this work, the performance of the correction algorithm is tested and compared to third-order sequential FM correction.

Methods

A healthy patient was scanned on a 7T head-only MRI (Siemens). Diffusion-weighted single-shot spiral acquisitions were performed with a parallel imaging acceleration factor of 4. The imaging parameters were: (FOV: 192 x 192 mm², in-plane resolution: 1.5 x 1.5 mm², slice thickness: 3 mm, number of slices: 10, TE/TR: 33/2,500 ms, BW: 2,170 Hz/pixel, flip angle: 70°, b = 0 s/mm² acquisitions: 1, diffusion directions: 6, b-value: 1000 s/mm²). B₀ field maps (in-plane resolution: 1.5 mm, slice thickness: 3 mm) were acquired for inclusion in a model-based image reconstruction⁶. FM was performed simultaneously using 16 transmit/receive ¹⁹F commercial field probes (Skope) that are integrated into a 32-channel RF head coil⁷. Image reconstruction was performed in MATLAB using in-house developed software that uses an iterative expanded encoding model-based reconstruction¹. Images were reconstructed using up to third-order k-coefficients that were generated and corrected using the algorithm described in Figure 1. Reconstructions using subsets of the three steps of the correction were also performed to determine each component’s efficacy. For comparison to sequential FM correction, images were corrected using FM data from an identical acquisition acquired when field probes were situated on the manufacturer’s scaffold.

Results

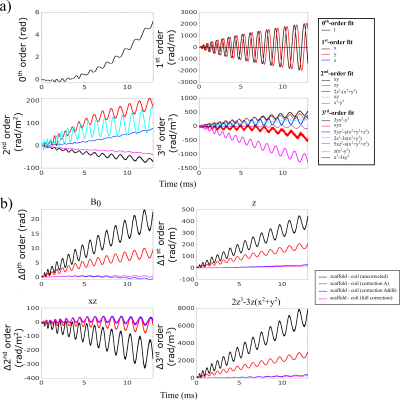
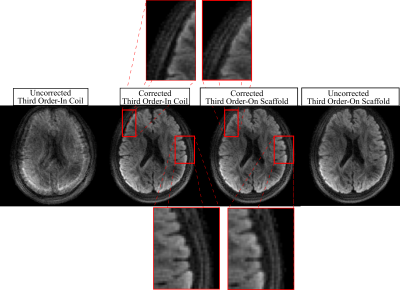
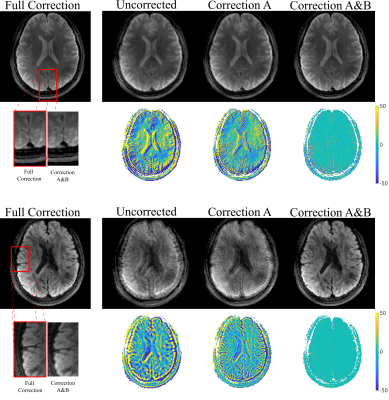
The difference in k-coefficients relative to the third-order scaffold fit (Fig. 2a) decreased significantly from the uncorrected case to correction A and also to correction A&B (Fig. 2b). Small differences were also observed when adding weighted least squares to obtain the full correction. In Figure 3, full correction showed significant improvement for a diffusion weighted image (DWI), while the correction improvement for the scaffold case was incremental. Overall reduction in blurring was observed for the corrected in-coil image relative to the corrected on-scaffold image. Figure 4 illustrates for a b = 0 image and DWI the effectiveness of each correction technique, with the addition of the first two correction steps noticeably reducing the error relative to the “gold standard” fully corrected image.

Discussion

Overall, images showed less blurring for concurrent monitoring with correction compared to sequential monitoring (with or without correction) (Fig. 3). This observation shows the added benefits of concurrent FM, which corrects for time-varying effects like frequency drift due to heating. The incremental improvement to image quality of scaffold data was expected due to the scaffold’s accurate measurements. The utility of GNL correction is evidenced by the reduction in the k-coefficient difference relative to the uncorrected case. This is further demonstrated by the higher quality of GNL-corrected images (Fig. 4). The step-wise estimation of k(t) shows substantial improvement in image quality, suggesting that it provides the largest benefit of the three strategies employed. Accordingly, solving k(t) one order at a time allows for a more accurate estimation of each order, while reducing the chances of over/under-fitting lower order terms. While not having a substantial effect on correction, the weighted least squares fit nevertheless helped decrease blurring (Fig. 4).

Conclusion

A correction algorithm that successfully improves the reliability of higher order concurrent FM data is presented and validated. This motivates the production of reproducible images for anatomical and functional imaging, as shown by spiral DWI presented in this work.

Acknowledgements

This work has been supported by the Natural Sciences and Engineering Research Council of Canada (NSERC), Canada Research Chairs, Canada First Research Excellence Fund to BrainsCAN, and the NSERC PGS D program.