1666
Theoretical Considerations on Joint Inference of Cardiac Diffusion and Strain Tensors from second-order motion compensated cDTI Data
Jonathan Weine1, Stefano Buoso1, and Sebastian Kozerke1
1Institute for Biomedical Engineering, University and ETH Zurich, Zürich, Switzerland
1Institute for Biomedical Engineering, University and ETH Zurich, Zürich, Switzerland
Synopsis
Cardiac diffusion tensor imaging (cDTI) as well as cardiac strain imaging both offer invaluable information on the functional state of the heart. Acquiring both, takes too long to be clinically feasible. Free breathing, cDTI acquisition with second-order motion compensated diffusion encoding waveforms display residual phase variations, that encode higher orders of contractile motion during the diffusion encoding process. This work presents a theoretical framework on how to jointly infer strain and diffusion tensors from complex-valued cDTI data with varying trigger delays.
Introduction
Cardiac Diffusion Tensor Imaging (cDTI) provides invaluable information about the state of myocardial microstructure in both healthy and diseased conditions1–4. To address signal loss due to contractile motion during the diffusion encoding process, second-order motion-compensated (M012) diffusion waveforms with spin-echo sequences have been established5. The signal loss occurs due to the spatial gradient of phase directly relating to myocardial strain6, which potentially can serve as indicator of pathological cardiac function7–9. For myocardial material point trajectories with motion terms higher than second order, the phase of cDTI data contains surrogate motion related to macroscopic strain. At the same time, macroscopic strain during diffusion encoding affects diffusion tensor estimation6 and hence needs to be taken into account. Therefore, it is appealing to aim at deriving both diffusion and strain information from a single cDTI exam.In this study we investigate the feasibility of jointly deriving strain and diffusion tensors from complex-valued M012-SE cDTI data. To this end, we present a theoretical framework for a simplified analytical motion model as well as general contractile motion. Furthermore, we show how our simulation allows the direct evaluation of the strain tensor for an analytic trajectory as well as the generation of labeled data for realistic contractile motion.
Methods
Cardiac modelThe digital phantom used in this work, is based on a biophysical mesh model of a contracting left ventricle (LV)10. Prior to simulation the mesh was refined, and a subset of nodes was selected forming a slice of 8 mm thickness perpendicular to the LV-long-axis. Random smoothly varying diffusion tensors were assigned to each mesh node11. Two trajectories $$$\mathbf{r}_{i,analytic}(t)$$$ and $$$\mathbf{r}_{i, realistic}(t)$$$ were assigned to each node, where $$$\mathbf{r}_{i,realistic}(t)$$$ was obtained from biophysical simulation and $$$\mathbf{r}_{i,analytic}(t)=\mathbf{r}_{i,0}+\mathbf{k(r_{i,0})}\sin(ct)$$$ describes planar, radial pseudo contractile motion.
Theory
Assuming separation of the scales for contractile macroscopic motion and microscopic tissue diffusion, one can describe the diffusion effect as magnitude attenuation and the contractile motion as a phase effect. Further assuming a material point representing an ensemble of spins is assigned a diffusion tensor and a motion trajectory, then the phase of a material point, after applying diffusion gradient $$$g_j(t)$$$ evaluates as:
$$\phi_j(\tau,\mathbf{r_0})=\gamma\int_0^Tg_j(t)\mathbf{r}(t-\tau,\mathbf{r_0})\cdot\mathbf{n}_jdt,$$
where $$$\tau$$$ denotes the trigger delay. Furthermore, the displacement $$$\mathbf{u}(\tau, \mathbf{r_0};T)$$$ of a material point at $$$\mathbf{r_0}$$$ during the encoding period $$$T$$$ is given as:
$$\mathbf{u}(\tau,\mathbf{r_0};T)=\mathbf{r}(\tau+T,\mathbf{r_0})-\mathbf{r}(\tau,\mathbf{r_0}).$$
Simplified analytic motion model
For $$$\mathbf{r}_{i, analytic}(t)$$$, the relation between phase and displacement can be derived directly with following steps:
- Replace $$$\mathbf{r}(t-\tau,\mathbf{r}{0})(t)$$$by its Taylor expansion in equation (1)
- All terms of the integral with quadratic or lower order in $$$t$$$ evaluate to zero, yielding a direct relation between the phase and the spatially varying amplitude $$$\mathbf{k(r_0)}$$$
- Insert $$$\mathbf{r}_{analytic}(t)$$$ into equation (2) and replace $$$\mathbf{k(r_0)}$$$ with the expression obtained fro the previous step, which yields:
General contractile motion
A relation between the displacement and the phase of diffusion encoded images for non-parameterized motion can be obtained by the following steps:
- Assume the Taylor expansion $$$\mathbf{r}(t,\mathbf{r_0})\approx\mathbf{r_0}+\mathbf{v(r_0)}t+\mathbf{a{r_0}}t^2+\mathbf{j(r_0)}t^3$$$ describes the trajectory of material points in the myocardium. Again, using the second order motion compensation of the waveform, the residual phase encodes the jerk $$$\mathbf{j_0}$$$ according to: $$\phi_j(\tau,\mathbf{r_0})=\gamma\mathbf{n}_j\cdot\mathbf{j_0}\int_0^Tg(t)(t-\tau)^3dt$$
- Evaluate the derivative of displacement (2) with respect to the trigger delay $$$\tau$$$, where $$$\mathbf{r}(\tau+T,\mathbf{r_0})$$$ and $$$\mathbf{r}(\tau,\mathbf{r_0})$$$ are approximated using the Taylor expansion: $$\frac{\partial\mathbf{u}(\tau,\mathbf{r_0};T)}{\partial\tau}\approx2T\mathbf{a(r_0)}+\mathbf{j(r_0)}[3T^2+6T\tau]$$
- From combining the two previous expression follows: $$\mathbf{n}_j\cdot\mathbf{u}(\tau,\mathbf{r_0})=2T\tau(\mathbf{n}_j\cdot\mathbf{a(r_0)})+(\mathbf{n}_j\cdot\mathbf{c(r_0)})+\int\phi_j(\tau,\mathbf{r_0})\frac{3T^2+6T\tau}{\gamma\int_0^Tg(t)(t-\tau)^3 dt}d\tau$$
A graphical summary of the simulation experiments for $$$\mathbf{r}_{i,analytic}(t)$$$ as well as $$$\mathbf{r}_{i,realistic}$$$ is given in Fig. 1. Simulation was performed by evaluating (1) on a temporal grid with $$$\Delta t=0.1ms$$$ for all mesh points, where the diffusion gradient was defined according to Stoeck et al.5 Furthermore, for each particle with the associated diffusion tensor $$$\mathbf{D}$$$, the factor $$$\exp(-b\mathbf{n^T}_j\mathbf{D}\mathbf{n}_j)$$$ was evaluated. This is followed by a single shot echo planar imaging readout. To obtain reference displacements on image resolution, a displacement encoding simulation was performed in the same fashion. Both simulations were repeated for varying trigger-delays for $$$\mathbf{r}_{i,analytic}(t)$$$ as well as $$$\mathbf{r}_{i,realistic}$$$. Additionally, the direct inversion according to equation (4) was performed using varying SNR values during simulation.
Results
Figure 2 illustrates the simulated motion trajectories. Simulation results for displacement encoding and diffusion weighted images are shown in Fig. 3. The displacement fields derived from displacement encoding and the ones from solving equation (4) for for multiple SNRs are presented in Fig. 4. Figure 5 shows a qualitative comparison of in-vivo data and the simulated signal with biophysically modelled contractile motion.Discussion
The simulation results for analytic motion show the feasibility of deriving both macroscopic strain and microscopic tissue diffusion from the same cDTI imaging protocol. Furthermore, the qualitative comparison of image phase across the LV for in vivo data and our simulation using the biophysical LV model yields qualitative agreement. The relation of displacements and residual phase in cDTI data is very complex as the provided theory demonstrates. Therefore, directly inferring the displacements from real data might be challenging especially when including respiratory motion and assuming low SNR. Training neural networks to perform such inversions on synthetic data was shown to be feasible11,12. Hence, training a neural network on our simulated data appears a promising next step.Acknowledgements
No acknowledgement found.References
1. Nielles-Vallespin S, Scott A, Ferreira P, Khalique Z, Pennell D, Firmin D. Cardiac Diffusion: Technique and Practical Applications. J Magn Reson Imaging 2019 doi: 10.1002/jmri.26912.
2. Mekkaoui C, Reese TG, Jackowski MP, Bhat H, Sosnovik DE. Diffusion MRI in the heart. NMR Biomed 2017;30 doi: 10.1002/nbm.3426.
3. von Deuster C, Sammut E, Asner L, et al. Studying Dynamic Myofiber Aggregate Reorientation in Dilated Cardiomyopathy Using In Vivo Magnetic Resonance Diffusion Tensor Imaging. Circ Cardiovasc Imaging 2016;9 doi: 10.1161/CIRCIMAGING.116.005018.
4. Gotschy A, von Deuster C, Weber L, et al. CMR Diffusion Tensor Imaging Provides Novel Imaging Markers of Adverse Myocardial Remodeling in Aortic Stenosis. JACC Cardiovasc. Imaging 2021;14:1472–1474 doi: https://doi.org/10.1016/j.jcmg.2020.12.026.
5. Stoeck CT, von Deuster C, Genet M, Atkinson D, Kozerke S. Second-order motion-compensated spin echo diffusion tensor imaging of the human heart. Magn Reson Med 2016;75:1669–1676 doi: 10.1002/mrm.25784.
6. Stoeck CT, Kalinowska A, von Deuster C, et al. Dual-phase cardiac diffusion tensor imaging with strain correction. PLoS One 2014;9:e107159 doi: 10.1371/journal.pone.0107159.
7. Scatteia A, Baritussio A, Bucciarelli-Ducci C. Strain imaging using cardiac magnetic resonance. Heart Fail. Rev. 2017;22:465–476 doi: 10.1007/s10741-017-9621-8.
8. Neizel M, Lossnitzer D, Korosoglou G, et al. Strain-encoded (SENC) magnetic resonance imaging to evaluate regional heterogeneity of myocardial strain in healthy volunteers: Comparison with conventional tagging. J. Magn. Reson. Imaging 2009;29:99–105 doi: https://doi.org/10.1002/jmri.21612.
9. Smiseth OA, Torp H, Opdahl A, Haugaa KH, Urheim S. Myocardial strain imaging: how useful is it in clinical decision making? Eur. Heart J. 2016;37:1196–1207 doi: 10.1093/eurheartj/ehv529.
10. S. Buoso, T. Joyce, and S. Kozerke. Personalising
left-ventricular biophysical models of the heart using parametric
physics-informed neural networks, Medical Image Analysis 2021, p. 102066
11. Weine J, van Gorkum RJH, Stoeck CT, Vishnevskiy V, Joyce T, Kozerke S. Inferring Diffusion Tensors on Unregistered Cardiac DWI Using a Residual CNN and implicitly modelled Data Prior. In: Annual meeting ISMRM. ; 2021.
12. Chen D, Schaeffter T, Kolbitsch C, Kofler A. Ground-truth-free deep learning for artefacts reduction in 2D radial cardiac cine MRI using a synthetically generated dataset. Phys. Med. Biol. 2021;66:095005 doi: 10.1088/1361-6560/abf278.
Figures

Figure 1: Flow chart summarizing the
simulation framework. Gray and blue arrows indicate the paths for the
analytical and realistic motion models respectively.

Figure 2: Representation of motion $$$\mathbf{r}_{analytic}(t)$$$ (left) and $$$\mathbf{r}_{realistic}(t)$$$ (right) in short axis view as a function of
trigger delay $$$\tau$$$. The images were obtained by evaluating the simulation with
a b-factor of $$$0 s/mm^2$$$.

Figure 3: Simulation results for $$$\mathbf{r}_{analytic}(t)$$$ with increasing trigger delay
$$$\tau$$$. Magnitude (top row) and phase (bottom row) for displacement encoding in
x and y direction (column 1-2 from left). Magnitude and phase of diffusion weighted images
for 3 exemplary diffusion directions (columns 3-5 from left).
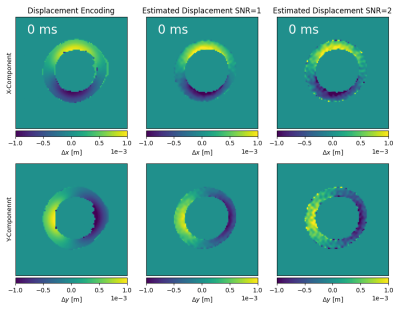
Figure 4: Displacements in x, y direction calculated from noise-less displacement encoding (left column) and by
solving equation (4) using the phase from diffusion weighted images for
multiple SNR 50 (middle column) and SNR 20 (right column).
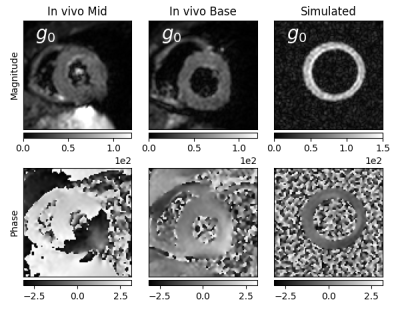
Figure 5: Comparison of magnitude and phase for an in-vivo dataset and our simulation
using the biophysically modeled contractile motion. Each frame shows a single
acquired average of one diffusion direction.
DOI: https://doi.org/10.58530/2022/1666