Introduction

Left ventricular (LV) ejection fraction (LVEF) is a strong predictor of outcome in patients with heart failure.¹ Cardiac magnetic resonance (CMR) is the gold-standard for LVEF assessment and typically involves the acquisition of a stack of LV short-axis 2D cine-images over multiple breath-holds. However, the low through-plane spatial resolution and coverage may be suboptimal for accurate assessment of LVEF.² Moreover, repeated breath-hold acquisitions may lead to poor reproducibility of end-inspiration position, are often challenging for patients, and may even cause Valsalva maneuvers resulting in biased LVEF measurements. In addition, operator involvement remains considerable as several cardiac localizers are still necessary to find the short-axis view. The free-running framework (FRF)³ was recently proposed to remove these constraints and to simplify workflow of LVEF assessment.⁴ However, the accuracy of FRF to assess LVEF has yet to be quantitatively examined. To reconstruct the highly undersampled 3D+cardiac+respiratory motion-resolved (5D) images, FRF requires careful optimization of the regularization weights to find a compromise between residual aliasing and compression of the underlying physiological motion. This work rigorously quantifies and optimizes the effect of the regularization weights on LVEF and several image quality metrics using a numerical phantom with well-controlled boundary conditions, and validates the results in in-vivo 5D FRF data.

Methods

Numerical Phantom: Free-running 3D golden-angle radial data were synthesized using a previously described numerical simulation.⁵ The synthesized data simulated anatomical tissues with realistic nonrigid cardiac and respiratory motion derived from the XCAT phantom⁶ and included heart-rate and respiratory motion variability. The simulated LVEF was 63.2%. The n-th radial readout corresponding to the (n-1)*TR timepoint was obtained by computing the 3D volume representing the desired cardiac and respiratory phase using the XCAT software, converting the labelled volume to CMR contrast using a bSSFP signal model with tissue relaxation properties from the literature, simulating 3D coil sensitivities, and computing the inverse NUFFT.⁵
Image reconstruction: The synthetic FRF radial data were sorted into a 5D (x-y-z-cardiac-respiratory) matrix and reconstructed with the compressed sensing (CS) reconstruction framework shown in Fig.1. The reconstruction implemented total variation (TV) and local low-rank (LR) regularization terms along both the cardiac and respiratory dimensions. The four corresponding regularization weights were the independent variables that were optimized as described below.
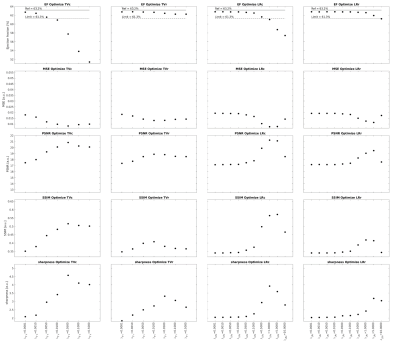
Analysis: LVEF was automatically computed for every reconstructed dataset using thresholding and the ground truth position of the aortic and mitral valves. The image quality was quantitatively assessed by the following metrics: mean squared error (MSE), structural similarity index measure (SSIM), peak signal-to-noise ratio (PSNR), and blood-myocardium interface sharpness. The four regularization terms were first optimized individually by setting the other terms to zero. For each term, the two regularization weights that yielded the highest image quality with an LVEF error below 3% when compared to ground truth were selected for further optimization. The 3% limit is well within the range of intra and interobserver variability of LVEF reported in earlier studies.² Next, the four regularization terms were optimized by combining the weights previously selected. The optimal combination of weights was determined by selecting the combination that resulted in the best image quality given a maximum acceptable LVEF error of 3%. Finally, as a proof of concept, the optimized combination was used to reconstruct an in-vivo 5D FRF dataset⁴ and the LVEF was compared to a reconstruction using weights that were optimized for image quality only without considering the maximum acceptable error limit for LVEF.

Results

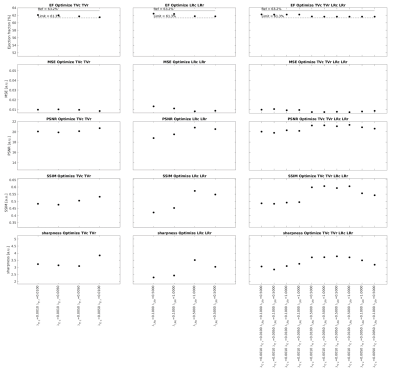
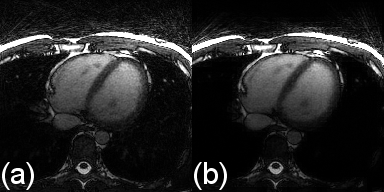
Increasing the regularization weights generally resulted in a decrease in LVEF and an improvement in image quality to a point beyond which image quality degraded again (Fig.2). Regularization along the respiratory dimension had a significantly lower impact on LVEF and image quality than regularization along the cardiac dimension, i.e. lower value spread (Fig.2). High respiratory regularization weights had little impact on LVEF, but significantly compressed respiratory motion (almost no visible respiratory motion for $$$\lambda_{TV_r}$$$=0.5 and $$$\lambda_{LR_r}$$$=10 in Fig.3). The optimization of each individual regularization term resulted in the following weights: $$$\lambda_{TV_c}$$$={0.001,0.005}, $$$\lambda_{TV_r}$$$={0.005,0.01}, $$$\lambda_{LR_c}$$$={0.1,0.5}, and $$$\lambda_{LR_r}$$$={0.5,1.0}. All possible combinations of the regularization terms with these weights resulted in an LVEF error of less than 3% (Fig.4). Among all these combinations, the one that gave the best image quality was ($$$\lambda_{TV_c}$$$,$$$\lambda_{TV_r}$$$,$$$\lambda_{LR_c}$$$,$$$\lambda_{LR_r}$$$)=(0.001,0.01,0.5,0.5). Reconstruction of the in-vivo FRF dataset using this optimized combination of weights resulted in 50.04% LVEF. When using the set of weights that maximizes image quality without considering LVEF error, i.e. ($$$\lambda_{TV_c}$$$,$$$\lambda_{TV_r}$$$,$$$\lambda_{LR_c}$$$,$$$\lambda_{LR_r}$$$)=(0.05,0.01,1.0,1.0), the LVEF was 44.87% in this case.

Discussion and Conclusion

This experimental study rigorously quantified and optimized the effect of the regularization weights of a CS reconstruction on the LVEF and several image quality metrics using a numerical phantom with well-controlled boundaries. The results demonstrated that the combination of regularization weights that are optimal in terms of image quality do not correspond to the optimal weights for LVEF assessment. Increasing the regularization weights generally resulted in better image quality, but also decreased LVEF accuracy due to motion compression artifacts. A relatively wide range of parameters provided an acceptable tradeoff between LVEF accuracy and image quality. This study may help guide reconstruction parameters for CS reconstruction of free-running 5D images and may help bridge a gap in validating optimized FRF for LVEF assessment.

Acknowledgements

No acknowledgement found.