1644
Amortised inference in diffusion MRI biophysical models using artificial neural networks and simulation-based frameworks1Sir Peter Mansfield Imaging Centre, Mental Health and Clinical Neurosciences, School of Medicine, University of Nottingham, Nottingham, United Kingdom, Nottingham, United Kingdom, 2Precision Imaging Beacon, University of Nottingham, Nottingham, United Kingdom, 3School of Mathematics, University of Nottingham, Nottingham, United Kingdom, 4Sir Peter Mansfield Imaging Centre, Mental Health and Clinical Neurosciences, School of Medicine, University of Nottingham, Nottingham, United Kingdom, 5Wellcome Centre for Integrative Neuroimaging, University of Oxford, Oxford, United Kingdom
Synopsis
Inference in imaging-based biophysical modelling provides a principled way of estimating model parameters, but also assessing confidence/uncertainty on results, quantifying noise effects and aiding experimental design. Traditional approaches in neuroimaging can either be very computationally expensive (e.g., Bayesian) or suitable to only certain assumptions (e.g., bootstrapping). We present a simulation-based inference approach to estimate diffusion MRI model parameters and their uncertainty. This novel framework trains a neural network to learn a Bayesian model inversion, allowing inference given unseen data. Results show a high level of agreement with conventional Markov-Chain-Monte-Carlo estimates, while offering 2-3 orders of magnitude speed-ups and inference amortisation.
Introduction
Inference and uncertainty quantification in imaging-based modelling provides a principled way of estimating non-linear model parameters, but also assessing confidence on results (1), quantifying noise effects (2) and aiding experimental design (3). In diffusion MRI (dMRI), it can assess precision of tissue microstructure estimates, while allowing probabilistic estimation of white-matter tracts (2). Traditional approaches for inference and uncertainty quantification include iterative bootstrapping (4) or Bayesian inference (5, 6). However, given the high data dimensionality with modern dMRI protocols (e.g., (7)), the large space of parameters and/or the lack of tractable likelihoods in some cases, traditional approaches can be slow, computationally demanding or, practically, unusable.Simulation-based inference (SBI) uses forward models to provide a data-driven alternative to classical inference based on training an artificial neural network (ANN) to learn posterior distributions (or approximate likelihoods), avoiding the requirement of likelihood calculations. We present here a first application of SBI in voxel-wise microstructural modelling and uncertainty quantification for dMRI data.
Methods
We designed an SBI framework for a dMRI biophysical model and compared it against a conventional Bayesian inference approach using Markov-Chain-Monte-Carlo (MCMC). In both approaches, our goal is to estimate the posterior distribution of the model parameters $$$\theta$$$ given data $$$x$$$, $$$P(\theta|x) ~ P(x|\theta)P(\theta)$$$ (Fig.1). In classical inference, this is done by inverting the forward model using approximate/iterative approaches, like MCMC. In SBI, this is achieved by training an ANN to learn the mapping between parameters and the data, using training datasets simulated from the forward model $$$f_x(\theta)$$$. This subsequently allows inference of the posterior given new data from the trained network directly, without model inversion (amortised inference).SBI can be casted as a problem of neural density estimation (Fig.2A). A parametric model $$$Q_{\phi}$$$, that takes as inputs pairs of datapoints $$$(u,v)$$$, returns a conditional probability density $$$Q_{\phi}(u|v)$$$ that is an approximation to the true conditional density $$$P(u|v)$$$. This can be chosen to be any conditional density distribution, e.g., likelihood or posterior; when estimating the posterior it is known as Neural Posterior Estimator (NPE) (9).
Using an artificial neural network as the parametric model, and the simulator $$$f_x(\theta)$$$ to create a simulated training dataset {$$$\{\theta_N, x_n\}$$$, we can train $$$Q_{\phi}(\theta|x)$$$ by maximizing the total log probability, $$$\sum_{N}log Q_{\phi}(\theta_N|x_N)$$$, with respect to hyper-parameters $$$\phi$$$ (9). To obtain distributions rather than point estimates, conditional density estimators are usually embedded into the ANN, with Normalizing Flows one of the most flexible options (10). Importantly, the learnt model allows for amortised inference (Fig.2B), i.e., to automatically infer parameters and their uncertainty for new unseen data, instead of going through a numerical model inversion process again for each new dataset as in classical model fitting.
Without loss of generality, we evaluated the above framework using the Ball&Sticks model as an exemplar for $$$f_x(\theta)$$$. We generated data (b=1000 s/mm2, 64 directions), and we firstly optimised the NPE hyper-parameters. We explored a range of possible density estimators (MDN, MADE (11, 12), MAF (13), and NSF (14)), convergence depending on training data size, and parameter priors. Using the best configuration, we compared the SBI and the MCMC results in both simulated and real data. For all the experiments, we used the sbi Python toolbox (15), and we implemented a random-walk Metropolis-Hastings MCMC in Python.
Results
Hyperparameter OptimisationUsing the absolute percentage error between SBI estimates and ground-truth values in 1000 numerically-generated datasets as agreement criterion, the Neural Spline Flow (NSF) (14) showed the best performance compared to the other density estimators (Fig.3A). We also found that using uniform priors showed more stable results and faster convergence than using Gamma distributions for diffusivity (Fig.3B). Finally, we have found that using a set of N=106 training dMRI datasets was enough for the network to converge while keeping an affordable training time (Fig.3D).
Comparisons to MCMC – Numerically-generated data
We generated 1000 synthetic datasets with parameters varying as follows: d:[0-5e-3 mm2/s], f:[0-1], orientations:[α:0-π; β:0-2π rads], SNR:[5-50]. The scatter plots shown in Fig. 4B, 4C show the mean estimates obtained by MCMC and SBI, compared to ground-truth for these configurations and for different SNR levels. Both approaches provided accurate estimates, with accuracy slightly reducing for lower SNR as expected.
Comparisons to MCMC – Real brain data
In this case, the SBI estimates are compared directly to the MCMC outputs. There is a high level of agreement in mean estimates between both approaches (Fig.5A, B, C). (16)The tract bundles obtained by running XTRACT (16) (i.e., probabilistic tractography) using the fibre orientations provided by SBI also show a high correlation with those obtained from the MCMC approach.
Computational performance
In a single-CPU core, the training of the network required 113 hours. Inference for every new whole-brain unseen dataset (104x104x56 voxels) took ~10 minutes. Running MCMC took more than 100 hours for each dataset. This reflects a speed-up of 2-3 orders of magnitude in parameter inference once the network is trained.
Conclusion
We have provided a first demonstration of SBI in dMRI microstructural modelling. The SBI framework provides higher flexibility and major advantages in terms of computational efficiency with respect to classical approaches, such as the MCMC, while keeping the accuracy of estimation.Acknowledgements
JPMP is supported by a PhD studentship funded by the Precison Imaging Beacon of Excellence, University of Nottingham. SS is supported by the Wellcome Trust (217266/Z/19) and a European Research Council consolidator grant (ERC 101000969).References
1. Jones DK. 2003. Determining and visualizing uncertainty in estimates of fiber orientation from diffusion tensor MRI. Magnet Reson Med. 49(1):7–12
2. Behrens TEJ, Woolrich MW, Jenkinson M, Johansen-Berg H, Nunes RG, et al. 2003. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magnet Reson Med. 50(5):1077–88
3. Alexander DC. 2008. A general framework for experiment design in diffusion MRI and its application in measuring direct tissue‐microstructure features. Magnet Reson Med. 60(2):439–48
4. Pajevic S, Basser PJ. 2003. Parametric and non-parametric statistical analysis of DT-MRI data. J Magn Reson. 161(1):1–14
5. Behrens TEJ, Berg HJ, Jbabdi S, Rushworth MFS, Woolrich MW. 2007. Probabilistic diffusion tractography with multiple fibre orientations: What can we gain? Neuroimage. 34(1):144–55
6. Fonteijn HMJ, Verstraten FAJ, Norris DG. 2007. Probabilistic Inference on Q-ball Imaging Data. Ieee T Med Imaging. 26(11):1515–24
7. Sotiropoulos SN, Jbabdi S, Xu J, Andersson JL, Moeller S, et al. 2013. Advances in diffusion MRI acquisition and processing in the Human Connectome Project. Neuroimage. 80:125–43
8. Cranmer K, Brehmer J, Louppe G. 2020. The frontier of simulation-based inference. Proc National Acad Sci. 117(48):30055–62
9. Papamakarios G, Sterratt DC, Murray I. Sequential Neural Likelihood: Fast Likelihood-free Inference with Autoregressive Flows. , p. 12
10. Lakshminarayanan GP and EN and DJR and SM and B. 2021. Normalizing Flows for Probabilistic Modeling and Inference. JMLR. 22:1–64
11. Germain M, Gregor K, Murray I, Larochelle H. 2015. MADE: Masked Autoencoder for Distribution Estimation. Arxiv
12. Bishop CM. 1994. Mixture density networks
13. Papamakarios G, Pavlakou T, Murray I. 2017. Masked Autoregressive Flow for Density Estimation. Arxiv
14. Durkan C, Bekasov A, Murray I, Papamakarios G. 2019. Neural Spline Flows. arXiv:1906.04032 [cs, stat]
15. Tejero-Cantero A, Boelts J, Deistler M, Lueckmann J-M, Durkan C, et al. 2020. sbi: A toolkit for simulation-based inference. J Open Source Softw. 5(52):2505
16. Warrington S, Bryant KL, Khrapitchev AA, Sallet J, Charquero-Ballester M, et al. 2020. XTRACT - Standardised protocols for automated tractography in the human and macaque brain. Neuroimage. 217:116923Figures
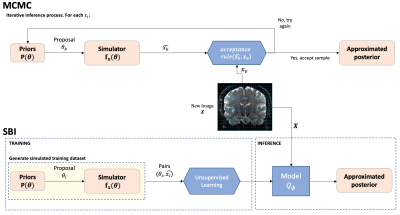
Fig. 1. Flow diagram comparison - Similarities (orange) and differences (blue) between SBI and MCMC. While in the MCMC the inference process is repeated k times for every voxel v, in SBI we simulate N measurements X={xi} with i=1…N, to train a model. This learnt model allows for amortised inference so it can be used to automatically infer the approximated posterior of the parameters for new data X.
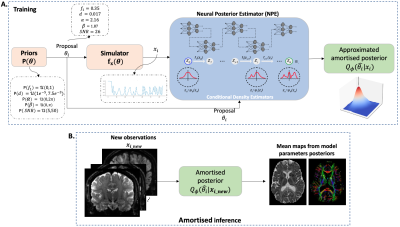
Fig. 2. Simulation-based inference framework - A. Using the priors $$$P(\theta)$$$, we can produce parameter proposals $$$\theta_i$$$, simulate the correspondent dMRI dataset $$$x_i$$$ and use it to train the NPE, that contains the Normalizing Flows embedded, to provide an approximated posterior density $$$Q_{\phi}(\hat{\theta_i}|x_i)$$$. B. The learnt posterior density $$$Q_{\phi}(\hat{\theta_i}|x_i)$$$ is amortised, i.e., if it is trained correctly, it can be used to infer the posterior density of parameters for any new observation $$$x_{i_new}$$$.
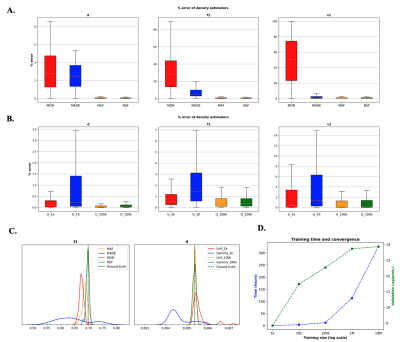
Fig. 3. Hyper-parameters optimisation - % absolute error between SBI estimates and ground-truth (N=1000 simulated datasets): A comparison between A. different density estimators, and B. different diffusivity priors, ![]() . C. Examples of posterior probability distributions returned for a single observation. D. Training metrics: time vs training size (red) and log(probability) in the validation set vs training size (green).
. C. Examples of posterior probability distributions returned for a single observation. D. Training metrics: time vs training size (red) and log(probability) in the validation set vs training size (green).
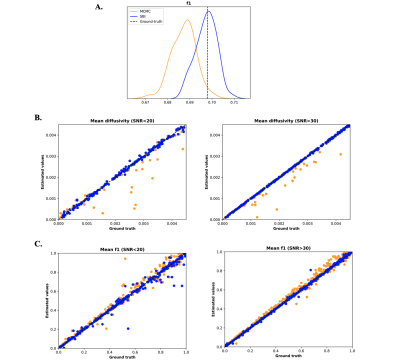
Fig. 4. Simulated data results – Comparison of MCMC (orange) and SBI (blue). A. f1 posterior distributions returned by the MCMC and SBI in a single dataset example. B, C. Scatter plot of MCMC and SBI estimates compared to the ground-truth of mean diffusivity d (B) and volume fraction (C) for low and high SNR levels.
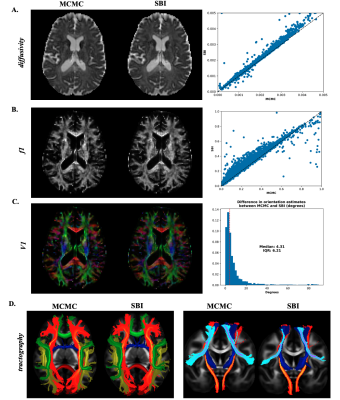
Fig. 5. Brain data results – Estimated mean maps using MCMC (left column) and SBI (middle column) for the diffusivity d (A), volume fraction f1 (B) and fibre orientation (C). The right column shows the scatter plot of the MCMC and SBI estimates for d and f1, and a histogram of the fibre orientation difference expressed in angle degrees. D. Probabilistic tractography of white matter tracts (axial and coronal views).