1639

Semi-supervised learning for fast multi-compartment relaxometry myelin water imaging (MCR-MWI)

Kwok-Shing Chan¹, Tae Hyung Kim^2,3, Berkin Bilgic^2,3, and José P Marques¹
¹Donders Institute for Brain, Cognition and Behaviour, Nijmegen, Netherlands, ²Athinoula A. Martinos Center for Biomedical Imaging, Charlestown, MA, United States, ³Department of Radiology, Harvard Medical School, Boston, MA, United States

Synopsis

Myelin water imaging using multi-compartment relaxometry (MCR-MWI) improves the GRE-MWI robustness and accuracy but suffered from slow processing speed. In this study, we incorporate both supervised and self-supervised machine learning for fast MCR-MWI that is generalisable to a wide range of acquisition parameters without the need to re-train the network. We demonstrate its application on single compartment fitting and MCR-MWI. Results show that the proposed method can produce comparable high SNR results with a 62-fold shorter processing time.

Introduction

Gradient echo myelin water imaging (GRE-MWI) is a promising myelination measurement method, yet highly ill-conditioned^1-3. A multi-compartment relaxometry method for MWI (MCR-MWI)⁴ incorporating variable flip angle (VFA), multi-echo GRE acquisition was recently introduced to overcome GRE-MWI limitations: accounting for distinct free water (IEW) and myelin water (MW) signal saturation, and ensuring fitting convergence. In MCR-MWI, the steady-state signal is modelled by the extended phase graph with exchange (EPG-X) framework⁵ to account for inter-compartmental magnetisation exchange. However, using EPG-X with non-linear least squares (NLS) fitting is computationally expensive. Without parallelisation, one 1.5-mm isotropic resolution brain volume requires ~350 computation hours.

Using fully-connected artificial neural networks (FC-ANN) to speed-up parameter mapping was previously implemented for MWI^6-7. However, these trained networks are protocol-specific and are not generalisable to new acquisition parameters (e.g., echo times). This would be even more critical with MCR-MWI where repetition time (TR), and (number of different) flip angles (α) have to be considered.

Self-supervised learning has been successful on rapid parameter mapping without the necessity of training data^8,9. We propose a semi-supervised learning method for MCR-MWI. An FC-ANN is trained as a fast EPG-X simulator to generate the IEW and MW steady-state signal. The trained FC-ANN is then embedded in the MCR-MWI model in a self-supervised network for parameter mapping¹⁰, utilising its computational efficiency to perform optimisation for a large number of voxels without extra training data, making it applicable across a variety of acquisition settings.

Methods

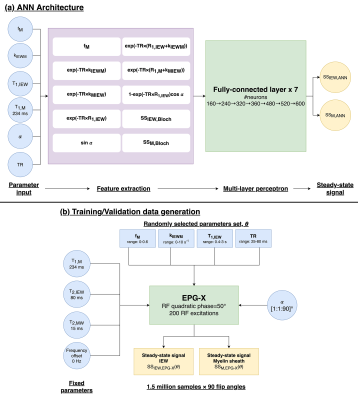
FC-ANN for EPG-X
The FC-ANN⁶ architecture for EPG-X is described in Fig.1. The network takes six inputs: myelin sheath volume fraction (f_M), T_1,IEW, T_1,M, exchange rate (k_IEWM), α, and TR, and returns the magnitude steady-state IEW and MW signals that match the EPG-X simulations.

Training data was generated from 1.5x10⁶ random parameter sets (θ) with the 4 parameters described in Fig.1b. Training was performed using Adam optimiser with 100 epochs. The training loss was defined as a sum of three mean squared errors (MSE):
$$loss=MSE_{\theta,\alpha}+MSE_{\theta,1-90}+{\lambda}MSE_{ds_\theta/d\alpha}$$
corresponding to the MSE between the FC-ANN predictions and the EPG-X signal (1) given θ at a single α ($$$MSE_{\theta,\alpha}$$$) and (2) for all 90 flip angles ($$$MSE_{\theta,1-90}$$$), and (3) the first derivative of the signal to flip angle ($$$MSE_{ds_\theta/d\alpha}$$$).

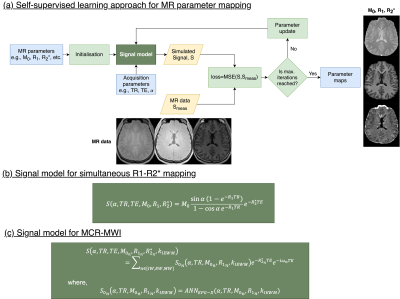
Self-supervised learning for parameter mapping
To perform parameter mapping, we deployed a simplistic physics-informed self-learning approach¹⁰ (Fig.2). The network is initialised with random (and/or constant) values for the MR parameters (which are the network parameters to be optimised) and the acquired MR data is given as input. During the learning process, signal is simulated given the parameters and the signal model (Fig.2b,c), and the MR parameters are updated using an Adam optimiser based on a loss function of the MSE between simulated and actual signal.

Both networks were created and trained using the Deep Learning Toolbox in Matlab R2021b (Natwick, US) with an NVIDIA Tesla P100 GPU (Santa Clara, CA).

In vivo imaging
Data acquisition was performed at 3T (Siemens, Erlangen) on 2 healthy volunteers. A monopolar 3D ME GRE sequence was used to acquire VFA data using two distinct sets of protocols
1) TR/TE1/ΔTE/nTE=38/2.2/3.07ms/12, TA=2.8min/α;
2) TR/TE1/ΔTE/nTE =55/2.68/3.95ms/13, TA=4min/α,
res=1.5mm iso., α=[5,10,20,50,70]°, R_CAIPI=5. B₁ map was acquired to correct the B₁ field inhomogeneity. The complex data of all different α datasets and the B₁ map were co-registered before further processing.

Single Compartment Relaxometry
As a reference standard fast processing pipeline, R₂* was estimated on each dataset using trapezoidal integration¹¹, followed by DESPOT1 R₁ mapping on the extrapolated S₀ images¹². Mean R₂* map was computed across flip angles. The self-supervised learning method shown in (Fig.2a,b) was used to demonstrate the network ability to perform simple parameter mapping.

Multi-Compartment Relaxometry
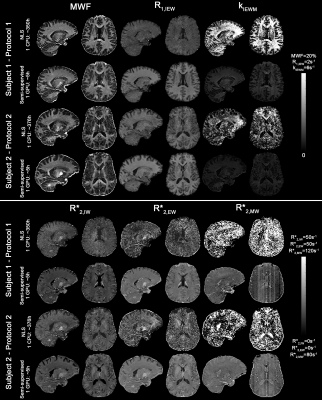
MWF maps were obtained as in ⁴ using an NLS fitting on a voxel-wise basis and compared to the self-supervised learning method described in (Fig.2a,c), processing ~12000 voxels simultaneously per batch.

The resulting maps between standard and self-supervised data were compared.

Results and Discussion

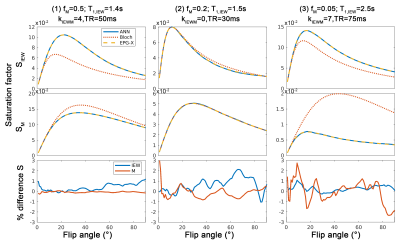
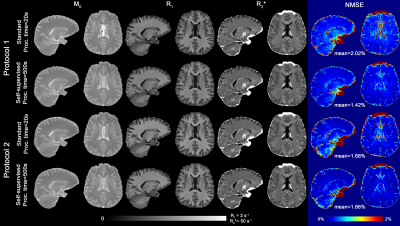
Fig.3 shows that the FC-ANN can generate the EPG-X signal for a variety of protocols and tissue parameters with the maximum percentage difference being below 3%.

Fig. 4 shows that the M₀, R₁* and R₂* maps derived from self-learning and standard relaxometry deliver comparable results, but the normalised MSE between the simulated and measured data is lower with the self-supervised method benefiting from its explicit MSE cost function.

Fig. 5 shows that the semi-supervised approach results in comparable MWF maps to voxel-wise fitting but 62-fold faster. Banding artefacts are observed in the most SNR sensitive measurements (R_2,MW* and k_IEWM) in regions corresponding to different processing batches. Although no explicit spatial regularization was used, the maps obtained are less prone to noise enhancement which is attributed to the learning gradients being computed over a large number of pixels.

Conclusions

We present a semi-supervised framework for MCR-MWI using an FC-ANN that is flexible to protocol settings (TR, TE and α) without re-training. Future work will explore the impact of learning rates associated with the various maps and introduce a 3DTV loss function to allow higher resolution MCR-MWI protocols. This framework can be adapted to complex non-linear fitting approaches as quantitative CEST or MT.

Acknowledgements

This work is part of the research programme with project number FOM-N-31/16PR1056/RadboudUniversity, which is financed by the Netherlands Organisation for Scientific Research (NWO). BB and THK are supported by research grants NIH R01 EB028797, R03 EB031175, U01 EB025162, P41 EB030006, U01 EB026996, and the NVidia Corporation for computing support.

References

1. Nam Y, Lee J, Hwang D, Kim D-H. Improved estimation of myelin water fraction using complex model fitting. Neuroimage 2015;116:214–221.

2. Alonso-Ortiz E, Levesque IR, Pike GB. Impact of magnetic susceptibility anisotropy at 3 T and 7 T on T2*-based myelin water fraction imaging. Neuroimage 2018;182:370–378.

3. Lee J, Nam Y, Choi JY, Kim EY, Oh S-H, Kim D-H. Mechanisms of T2 * anisotropy and gradient echo myelin water imaging. NMR in biomedicine 2016.

4. Chan K-S, Marques JP. Multi-compartment relaxometry and diffusion informed myelin water imaging – Promises and challenges of new gradient echo myelin water imaging methods. Neuroimage 2020;221:117159.

5. Malik SJ, Teixeira RPAG, Hajnal JV. Extended phase graph formalism for systems with magnetization transfer and exchange. Magnetic resonance in medicine 2017;3:125 doi: 10.1002/mrm.27040.

6. Lee J, Lee D, Choi JY, Shin D, Shin H-G, Lee J. Artificial neural network for myelin water imaging. Magnetic resonance in medicine 2019;31:673.

7. Jung S, Lee H, Ryu K, et al. Artificial neural network for multi‐echo gradient echo–based myelin water fraction estimation. Magnet Reson Med 2021;85:380–389.

8. Kang B, Kim B, Schär M, Park H, Heo H. Unsupervised learning for magnetization transfer contrast MR fingerprinting: Application to CEST and nuclear Overhauser enhancement imaging. Magnet Reson Med 2021;85:2040–2054.

9. So S, Kim B, Park H, Bilgic B. BUDA-STEAM: A rapid parameter estimation method for T₁, T₂, M₀, B₀ and B₁ using three-90° pulse sequence. In: Processing

30, Annual Meeting International Society for Magnetic Resonance in Medicine, Montreal, Canada, 0327 (2021).

10. Kim T, Cho J, Zhao B, Bilgic B. MR parameter mapping with unsupervised scan-specific neural networks. Workshop on MRI Acquistion & Reconstruction, Virtual meeting (2021)

11. Gil R, Khabipova D, Zwiers M, Hilbert T, Kober T, Marques JP. An in vivo study of the orientation-dependent and independent components of transverse relaxation rates in white matter. NMR in biomedicine 2016;29:1780–1790.

12. Deoni SCL, Rutt BK, Peters TM. Rapid combinedT1 andT2 mapping using gradient recalled acquisition in the steady state. Magnet Reson Med 2003;49:515–526.

Figures

Fig. 1: a) The EPG-X steady-state FC-ANN is preceded by a feature extraction step to derive 10 input features that are both normalized to [0,1] and are related with different terms of the Bloch-McConnell equations. The network core comprises 7 hidden fully-connected layers and a leaky RELU (scale factor=0.01) function. The network parameters are trained with a hybrid strategy of increasing batch size and reducing learning rate as a function of the training iterations to ensure convergence. b) Illustration of the parameters and their ranges to generate training and validation data.

Fig. 2: (a) Illustration of the self-supervised method for parameter mapping. This network uses a signal model to generate simulated data that minimises the MSE to the measured data, and MR parameters are updated until the maximum number of iterations is reached. This method can be adopted for various parameter mapping methods by incorporating the corresponding signal model. We demonstrated its applications on (b) single compartment mapping and (c) MCR-MWI incorporating the network in Fig.1. Contrary to voxel-wise fitting, the proposed method operates on volumetric inputs.

Fig. 3: Plots of the steady-state signal (at TE=0) using the standard Bloch equations (dot), EPG-X (dashed) and FC-ANN (solid) as a function of flip angle. The columns show the simulations of 3 samples in the validation set with different TR and tissue properties. The top row shows the signal of free water, the middle row shows the signal of the myelin water. The bottom row shows the percentage difference of the FC-ANN in respect to EPG-X for the free water (blue) and myelin water (red) respectively. In most cases, the percentage difference from FC-ANN output is below 3%.

Fig. 4: Single compartment mapping using standard method (1^st & 3^rd rows) and self-supervised learning (2^nd& 4^th rows). Unsurprisingly, both methods produce maps with very similar contrast since the signal model is not ill-conditioned. Overall, lower normalised MSE can be observed in self-supervised results, particularly in CSF. In a simple problem likes this, the self-supervised method does not show the advantage of computational time.

Fig. 5: MCR-MWI results from voxel-wise fitting and semi-supervised learning on 2 subjects (only 1 protocol is shown). MWF maps from both methods share similar contrast in white matter. Significantly different R_1,IEW and k_IEWM are observed with semi-supervised learning, and its R_1,IEW looks closer to the R₁ in Fig.4. The compartmental R₂* show higher SNR with the proposed method, which likely benefits from having more data in the optimisation that makes the results less error-prone. Banding artefacts in R_2,MW* & k_IEWM are related to different processing batches.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

1639

DOI: https://doi.org/10.58530/2022/1639