1630
MR determination of the diffusion propagator: measurements on mouse spinal cord using a benchtop scanner1Department of Biomedical Engineering, Linköping University, Linköping, Sweden, 2Department of Biomedical and Clinical Sciences, Linköping University, Linköping, Sweden
Synopsis
We demonstrate the experimental determination of the diffusion propagator, indicating a conditional probability density function with two spatial arguments. To this end, a recently introduced method was implemented on a benchtop MR scanner and incorporated into imaging sequences. The data involving two independent wavenumbers were transformed from the measurement domain to the spatial domain, yielding an apparent diffusion propagator. Experiments on freely diffusing water provides accurate determination of the diffusion propagator while apparent propagators measured in mouse spinal cord reveal significant differences between white and gray matter regions.
Introduction & Theory
Recently, a novel technique for measuring the diffusion propagator was introduced1. The employed diffusion encoding gradient waveform (Figure 1a), reduces to the classic Stejskal-Tanner sequence2 for $$$\mathbf{q’ = -q}$$$ and to Laun et al.’s sequence3 for $$$\mathbf{q’}=0$$$. From the signal, $$$ E_\Delta(\mathbf{q},\mathbf{q}')$$$, acquired using this sequence, the propagator can be obtained through the expression1:$$P(\mathbf{x}',\Delta|\mathbf{x})=\frac{(2\pi)^{-2d}\int\mathrm{d}\mathbf{q}\, e^{i\mathbf{q}\cdot\mathbf{x}}\int\mathrm{d}\mathbf{q}'\, e^{i\mathbf{q}'\cdot\mathbf{x}'}\, E_\Delta(\mathbf{q},\mathbf{q}')}{(2\pi)^{-d} \int\mathrm{d}\mathbf{q}\,e^{i\mathbf{q}\cdot\mathbf{x}}\, E_\Delta(\mathbf{q},\mathbf{0})} \qquad (1)$$
where $$$d$$$ is the number of measurement dimensions. Compared to the ensemble average propagator available through the inverse Fourier transform of the Stejskal-Tanner signal, the above quantity has an extra spatial argument, thus could elucidate more information on the tissue structure1.
Here, we demonstrate the first experimental results on biological tissue obtained using this technique.
Methods
The pulse sequence presented in Figure 1b was implemented on a benchtop MRI scanner (Pure Devices GmbH, Germany). In our implementation, each diffusion gradient of the effective waveform in Figure 1a is replaced with a bipolar gradient pair to mitigate the effects of concomitant fields, susceptibility variations, and eddy currents4.Two samples were investigated: a water phantom as a proof-of-concept study for free diffusion; and a sample of mouse spinal cord (obtained following national and local ethical guidelines). This sample had approximately the following dimensions: $$$2\times 1.5\times2.5 mm^3$$$.
For the first sample, images were acquired with a matrix size of $$$16\times16$$$ over an FOV of $$$10\times10 mm^2$$$. The values of q and q’ applied in this study ranged from $$$-1.2 rad/\mu m$$$ to $$$+1.2 rad/\mu m$$$ with 21 linearly-spaced steps, yielding a total of 441 different measurements.
The acquired images of the SC sample had a matrix size of $$$48\times 96$$$ and an in-plane voxel size of approximately $$$0.15\times0.15 mm^2$$$. The values of q and q’ applied in this study ranged from $$$-0.8 rad/\mu m$$$ to $$$+0.8 rad/\mu m$$$ with 21 linearly-spaced steps, resulting in 441 different measurements.
Diffusion gradients in all experiments were applied along a single direction, and for the SC sample this direction was set perpendicular to the direction of the fibers in white matter. Furthermore, this acquisition was repeated 16 times, averaged, and filtered with a simple gaussian filter.
Data analysis for the water phantom involved the reconstruction of the propagator using magnitude-valued data. The reconstructed propagator was compared to the analytical expression of the apparent diffusion propagator (accounting for the parameters of the waveform) and the propagator reconstructed using simulated data obtained by the analytical signal sampled consistently with the acquisition protocol.
For the second study, complex data acquired from the scanner were used in the reconstruction pipeline. Furthermore, the real component of the 2D Fourier transform of the signal was used to obtain a mask for eliminating the noise-dominated voxels on the $$$xx’$$$ plane.
All computations were performed using MATLAB (Mathworks Inc., Natick, MA, USA).
Results
A $$$5\times5$$$ matrix of the normalized images acquired from the water phantom is presented in Figure 2. The reconstructed propagator for the center voxel of the acquired images, and the difference maps obtained with the analytical apparent propagator and the one reconstructed from simulated data are presented in Figure 3.A $$$7\times7$$$ matrix of the normalized images corresponding to the SC sample is presented in Figure 4. Furthermore, a proton density weighted image of the spinal cord sample with a higher in-plane resolution is presented in Figure 5a, and the real parts of the numerator and denominator of Equation 1, as well as the reconstructed propagator are shown in Figure 5b for a white matter (WM) and a gray matter (GM) voxel.
Discussion & Conclusion
The reconstructed propagator for free diffusion agrees with the apparent propagator obtained from the analytical expression for the signal as well as from simulated data. The peak in the center voxel of the measured propagator is due to the magnitude-valued data having Rician distribution.Compared to free diffusion, the apparent propagator for the spinal cord sample has limited extent, which is smaller in WM compared to GM. The pulse sequence reveals the superposition of propagators for each “bouquet” (containing particles having the same center-of-mass during the application of the long pulse) translated to a common origin4. Thus, the observed differences may be due to the presence of restricted diffusion in WM in the probed orientation (perpendicular to fibers). Furthermore, the elevated spread of propagator values in GM could be indicative of its complex architecture.
With the current implementation of our technique, we managed to successfully reconstruct apparent diffusion propagators for free diffusion as well as in mouse spinal cord. Due to the limited breadth of the propagators, the study could be performed with a smaller “FOV” in the $$$xx’$$$ plane, i.e., with samples in $$$qq’$$$ space separated apart. Nonetheless, the technique requires many measurements, thus long acquisition times, even when the gradients are applied in the same orientation. Therefore, a scheme for reducing the number of required samples could be tackled in future studies. The feasibility of the technique on a benchtop MRI scanner as illustrated here is encouraging for future translation of the method to other platforms including to clinical settings.
Acknowledgements
We are grateful to Deneb Boito and Magnus Herberthson for their feedback on the manuscript, and to Anders Eklund for his support in the acquisition of the MR scanner.References
[1] E. Özarslan, in Proc Intl Soc Mag Reson Med, Vol. 29 (2021) p. 3637.
[2] E. O. Stejskal and J. E. Tanner, J Chem Phys 42, 288 (1965).
[3] F. B. Laun, T. A. Kuder, W. Semmler, and B. Stieltjes, Phys Rev Lett 107, 048102 (2011).
[4] A. M. Ordinola Santisteban and E. Özarslan, arXiv:2106.16181 (2021).
Figures
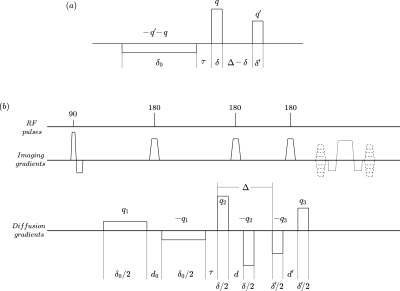
Figure 1
(a) Effective diffusion encoding gradient waveform introduced in [1].
(b) Implemented sequence with bipolar gradients. The areas under the diffusion gradient pulses are: $$$q_1=\frac{q+q'}{2}$$$, $$$q_2=\frac{q}{2}$$$ and $$$q_3=\frac{q'}{2}$$$, respectively. The delays between the two lobes of the bipolar gradients ($$$d_0, d, d'$$$) are the same for all pulse pairs. Imaging gradients enable slice selection (straight line), frequency encoding (dotted line), and phase encoding (dashed line).

Figure 2
Images acquired from the water phantom in a $$$5\times5$$$ matrix after three averages; each image is obtained with a single ($$$\tt q,\tt q'$$$) combination. Images were normalized with the image with no diffusion weighting. The plotted intensity values depict $$$\tanh(\pi*E_\Delta(q,q'))$$$ to accentuate low signal decay values at higher $$$\tt q$$$ and $$$\tt q'$$$. Time parameters: $$$\delta_0=20ms$$$, $$$\delta=\delta’=4ms$$$, $$$\Delta=10ms$$$, $$$\tau=3ms$$$, $$$d_0=d=d’=4ms$$$, $$$TE/TR=58/2000ms$$$.

Figure 3
(a) Center portion of the measured propagator $$$P(x',\Delta|x)$$$ for a single voxel of the acquired images of the free diffusion phantom. (b) Analytical apparent propagator $$$P_\mathrm{app}(x',\Delta|x)$$$. (c) Reconstructed propagator for simulated data $$$P_\mathrm {sim}(x',\Delta|x)$$$. Difference maps between (d) experimental and analytical apparent propagators and (e) experimental propagator and that reconstructed from simulated data.

Figure 4
Images acquired from the spinal cord sample in a $$$7\times7$$$ matrix after sixteen averages; each image is obtained with a single ($$$\tt q, \tt q'$$$) combination. Images were normalized with the maximum value of the whole dataset. Time parameters: $$$\delta_0=10ms$$$, $$$\delta=\delta’=2ms$$$, $$$\Delta=8ms$$$, $$$\tau=3ms$$$, $$$d_0=d=d’=2ms$$$, $$$TE/TR=38/400ms$$$.
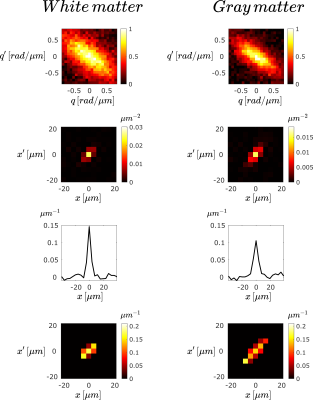
Figure 5
Real components of the quantities in the different steps of propagator estimation for a white-matter (left) and a gray-matter (right) voxel. From top to bottom: Signal decay, numerator of Eq. 1, denominator of Eq. 1, and center portion of the computed apparent propagator.