Introduction

Double diffusion encoding (DDE) schemes with two pairs of bipolar gradients separated by a refocusing pulse can be used to derive orientationally invariant metrics such as microscopic anisotropy^1,2. These sequences are prone to severe artifacts induced by concomitant fields resulting from Maxwell’s equations, which introduce an additional non-linear phase contribution on the transverse magnetization^3,4.

Recently, Maxwell field compensation in the context of DDE was demonstrated by adding oscillating gradients⁵, which allows compensation of self-squared concomitant fields.

In this study, we present simulations to investigate the possibility to additionally compensate the cross terms occurring between the different physical scanner axes. This is enabled by adding oscillations to all gradient pulses for simultaneous diffusion weighting and concomitant field compensation and applying pulse-width modulation (PWM) to control diffusion weighting ($$$\mathrm{q}$$$- and $$$\mathrm{b}$$$-values).

Especially local gradient coils with ultra-high amplitudes are expected to create significant concomitant fields. On the other hand, oscillating gradients are easier to implement for local gradient coils^6,7 due to higher available slew rates and less peripheral nerve stimulation (PNS) problems.

Methods

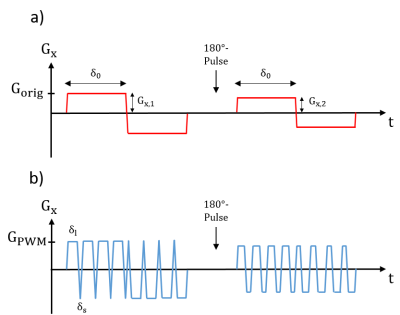
Simulations were performed using MATLAB (The Mathworks, Inc, MA). The presented framework was evaluated on 60 pairs of diffusion wave vectors published by Jespersen et al.².

The original diffusion weightings were replaced by oscillating gradients with pulse-width modulation for reduction of the concomitant phase (Figure 1), which is given by $$\mathrm{\phi_C(x,y,z)=\gamma\int B_C(x,y,z,t)\,dt.\quad[1]}$$ Here, $$$\gamma$$$ is the gyromagnetic ratio and $$$\mathrm{B_C(x,y,z,t)}$$$ are the concomitant fields, given to the lowest order by $$\mathrm{B_C(x,y,z,t)}=\frac{1}{2\mathrm{B_0}}(\mathrm{G_x^2z^2+G_y^2z^2+G_z^2\frac{x^2+y^2}{4}-G_xG_zxz-G_yG_zyz}).\quad[2]$$ The gradients $$$\mathrm{G_x}$$$,$$$\,$$$$$$\mathrm{G_y}$$$ and $$$\mathrm{G_z}$$$ modify the static magnetic field $$$\mathrm{\vec{B}_0=B_0\hat{e}_z}$$$ along the physical scanner axes $$$\mathrm{x}$$$, $$$\mathrm{y}$$$ and $$$\mathrm{z}$$$, respectively.

The first three self-squared terms in [2] are compensated when the respective gradients fulfill $$\mathrm{\int_0^{TE}s_n(t)\,G_i(t)^2\,dt=0,{\quad}i\in\{x,y,z\}},\quad[3]$$ with $$$\mathrm{TE}$$$ being the echo time and $$$\mathrm{s_n(t)=(-1)^{n_{rf}(t)}}$$$, where $$$\mathrm{n_{rf}(t)}$$$ is the number of refocusing pulses within time interval $$$\mathrm{t}$$$ to $$$\mathrm{TE}$$$.

The long and short duration of a modulated oscillation result from $$\mathrm{\delta_{l,s}=\delta_{+,-}=\frac{\delta_0}{2N}\left(1\pm\frac{G_{orig}}{G_{PWM}}+\frac{\epsilon}{\delta_0}\right)-\epsilon},\quad[4]$$ which ensures conservation of the $$$\mathrm{q}$$$-value and the total duration of the original gradient form.

For the given gradient rise time $$$\mathrm{\epsilon}$$$, the duration of the original diffusion gradient $$$\mathrm{\delta_0}$$$ and the number of its modulated oscillations $$$\mathrm{N}$$$, the ratio of the gradient amplitudes $$$\mathrm{G_{orig}}$$$ and $$$\mathrm{G_{PWM}}$$$ of the original and modulated gradient form, respectively, must fulfill $$\mathrm{\frac{G_{orig}}{G_{PWM}}<\frac{(1-4N)\epsilon}{\delta_0}+1\quad[5]}$$ to guarantee non-negative flat top times for the oscillation lobes.

On a gradient axis, the gradient form with the highest amplitude undergoes a gradient-based optimization to determine $$$\mathrm{G_{PWM}}$$$, $$$\mathrm{\delta_l}$$$ and $$$\mathrm{\delta_s}$$$ with a minimal $$$\mathrm{b}$$$-value deviation and the constraint in [5]. The optimum for the same parameters for the lower amplitude gradients is then found with the objective of concomitant field compensation based on [3].

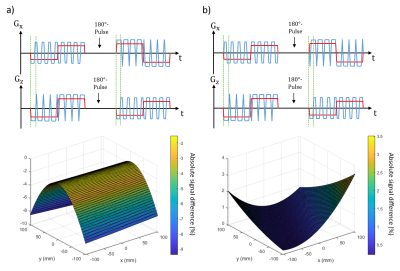
The modulated lobes on the gradient axes $$$\mathrm{x}$$$ and $$$\mathrm{y}$$$ are cyclically shifted by one oscillation lobe independently until the smallest impact of the resulting overlap integral on [1] of the last two cross terms in [2] is reached.

In the simulation, every direction within 60 wave vector pairs² applied a diffusion weighting of $$$\mathrm{b}=$$$$$$\,$$$500$$$\,$$$s/mm² with $$$\mathrm{\delta_0=}$$$$$$\,$$$15.96$$$\,$$$ms at a rise time of $$$\mathrm{\epsilon}=$$$$$$\,$$$0.4$$$\,$$$ms. The effect of the concomitant phase on the signal was evaluated numerically at $$$\mathrm{B_0=}$$$$$$\,$$$3$$$\,$$$T without modulation and for $$$\mathrm{N}=$$$$$$\,$$$4 for a transversal slice with a FOV of 210$$$\,$$$mm in both directions and a voxel size of 3$$$\,$$$$$$\times$$$$$$\,$$$3$$$\,$$$$$$\times$$$$$$\,$$$3$$$\,$$$mm³. The slice was shifted from the isocenter by $$$\mathrm{{\Delta}z}=$$$$$$\,$$$5$$$\,$$$cm.

Results

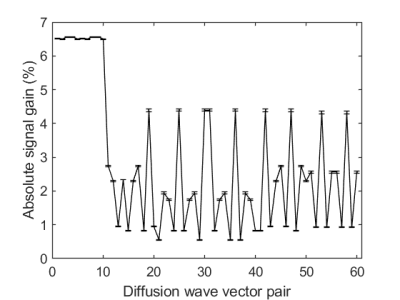
The proposed modulation leads to a gain in the averaged signal of the slice for all considered pairs of diffusion directions for the applied parameters (Figure 2). The achieved absolute signal gain of around 6.5$$$\,$$$% for the first direction pairs decreases due to growing influence of cross terms for the other direction pairs, but still remains positive due to the shifting of the modulated gradient lobes where necessary.

Figure 3 shows the effect of shifting the modulated lobes for an exemplary direction pair. While the self-squared concomitant fields are highly reduced, the cross term distribution leads to an overall signal loss (a). Shifting the modulated oscillations on the $$$\mathrm{x}$$$-axis cyclically reduces the effect of the cross terms and achieves a signal gain in the slice (b).

Discussion and Conclusion

As presented, using oscillating gradients with PWM and adequate temporal shifting enables concomitant field compensation with simultaneous diffusion weighting for arbitrary pairs of encoding wave vectors.

For the considered gradient direction pairs, modulation with four oscillations per gradient is expected to achieve signal improvement on average without exceeding a gradient amplitude of 80$$$\,$$$mT/m, which makes the method theoretically feasible on commercially available gradient systems.
To maintain this amplitude limit and comply with [5], the duration of the original diffusion gradients was increased by 4.37$$$\,$$$ms. The modulation leads to a maximum deviation in $$$\mathrm{b}$$$-value of 70$$$\,$$$s/mm², which can be reduced by using more oscillations setting higher requirements on the rise time and amplitude limit.
The effective diffusion time will not be substantially affected by the modulation due to two different durations within one oscillation period.

On whole-body systems, PNS may be a major issue for oscillating gradients, which will be less limiting for local gradient coils^6,7.

In conclusion, the proposed PWM can lead to a signal gain by reducing the influence of concomitant fields without the need for additional refocusing RF pulses.

Acknowledgements

No acknowledgement found.