1625

Phase Stabilization with Motion Compensated Gradient Waveforms for Brain Diffusion Weighted Imaging (DWI)
Ariel J Hannum1,2,3, Tyler E Cork1,2,3, Merlin J Fair1,2, Kawin Setsompop1,4, and Daniel B Ennis1,2
1Department of Radiology, Stanford University, Stanford, CA, United States, 2Division of Radiology, Veterans Administration Health Care System, Palo Alto, CA, United States, 3Department of Bioengineering, Stanford University, Stanford, CA, United States, 4Department of Electrical Engineering, Stanford University, Stanford, CA, United States

Synopsis

Conventional brain DWI acquisitions are sensitive to physiological motion, which causes shot-to-shot phase variations between images. This makes accelerated, multi-shot imaging harder to achieve. We propose that motion compensated gradient waveforms will improve shot-to-shot phase stability. We found that both velocity and acceleration gradient moment nulling, particularly when diffusion encoding along the z-axis, improves shot-to-shot phase consistency at different cardiac trigger-delay times and reduces phase variation between repetitions for a fixed trigger-delay. We conclude that motion-compensated diffusion encoding gradients improve the phase stability between image shots.

Introduction

The gradients used to encode the self-diffusion of water in diffusion weighted imaging (DWI) can encode unwanted phase from motion in the complex image. Bulk motion arises, for example, from cardiac induced pulsatility and fluid flow. This can induce brain tissue displacements on the order of hundreds of microns.1-4 Periodic motion during continuous DWI acquisitions contributes to shot-to-shot phase variations that make multi-shot acquisitions more challenging to reconstruct.5

Substantial improvements in reconstruction algorithms have made multi-shot imaging feasible in the brain, but it remains challenging due to phase inconsistencies.6, 7 For diffusion prepared sequences, a magnitude stabilizing gradient decreases phase variation, but at the cost of halving the signal.8 Alternatively, motion compensated gradient waveforms can mitigate the effects of bulk motion and incoherent tissue motion in cardiac diffusion-weighted MRI (DWI).9-11 For example, velocity moment nulling (M0M1) and acceleration moment nulling (M0M1M2) are used in cardiac DWI to mitigate magnitude dropout due to intravoxel dephasing.9,11,12 However, the degree to which these gradient waveforms improve phase consistency has yet to be fully investigated in the brain.

The objective of this work was to evaluate the phase stability using repeated acquisitions of three different diffusion encoding gradient waveforms (with and without motion compensation) for brain DWI at eight ECG-gated cardiac phases. We hypothesize that gradient moment nulling will reduce phase variations across repeated acquisitions.

Methods

Image Acquisition
After obtaining IRB-approved informed consent, five (n=5) volunteers were imaged via a 3T MRI (Skyra, Siemens, Erlangen, Germany) with a 20-channel head coil. Three axial brain slices (lower-brainstem, mid-basal ganglia, and upper-cortex) were acquired using an ECG-gated spin-echo single-shot echo planar imaging sequence (resolution=2.0×2.0×2.0mm3, GRAPPA=2, Partial Fourier=6/8, b-values=[0, 1000 s/mm2], three diffusion directions, five averages, TR=3xR-R-intervals, cardiac phases=8). Three different orders of motion compensation were used: M0, M0M1, and M0M1M2. The TEs for these gradient waveforms were 73ms, 106ms, and 144ms, respectively. The trigger delay (TD) time for each cardiac phase was calculated such that the refocusing pulses of the different motion compensated gradient waveforms were aligned.13

Analysis
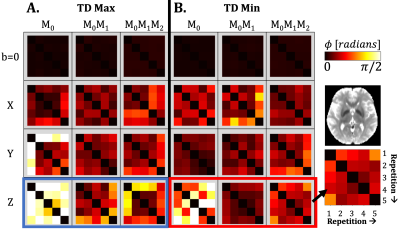
The average phase (Φavg) between repeated acquisitions at the same TD was computed using the angle of the complex average of the images. Phase differences (Φdiff) from Φavg were also calculated for each acquired image. The standard deviation (σdiff) of the phase differences was then computed and averaged for each TD across to identify minimum and maximum phase variations for the population. The voxel-by-voxel Pearson’s correlation coefficient of Φavg across different TDs was computed for the different motion compensated gradients.

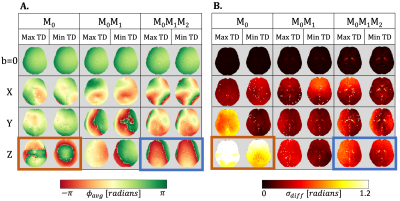
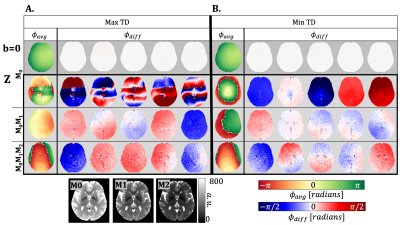
Results

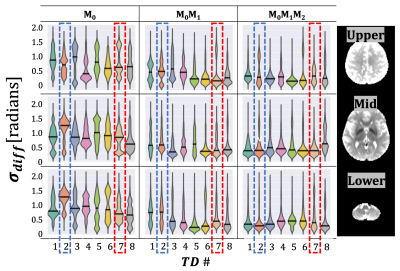
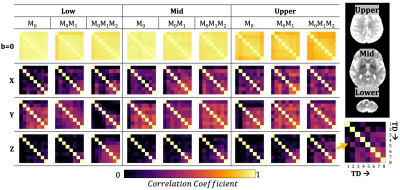
The TD with the maximum phase variation was 104±11ms, 114±11ms, and 122±11ms for M0, M0M1, and M0M1M2 gradients (TD-2). The TD with minimum phase variation was 626±11ms, 636±11ms, and 644±11ms for M0, M0M1, and M0M1M2 gradients (TD-7). The maximum TD and minimum TD were used to evaluate Φavg and σdiff. Qualitatively, we observed a stabilization in the phase for the z-direction when utilizing M0M1 and M0M1M2 compensation in comparison to M0(Figure 1). Φdiff was also reduced when M0M1 and M0M1M2 is included (Figure 2). The measured phase has better shot-to-shot phase consistency with the M0M1 and M0M1M2 compensated gradient waveforms. Furthermore, the phase across repeated acquisitions for one TD demonstrates how differences between individual repetitions are reduced (Figure 3).

Phase consistency across all TDs was assessed by evaluating the distribution of the σdiff at different TDs in violin plots (Figure 4) and correlation across different TDs (Figure 5). We observe that with M0, there is wider range of phase standard deviation values that is indicative of more shot-to-shot variation in the phase. These trends were consistent between different slices. With M0M1 and M0M1M2 compensated gradients, the distribution of σdiff is lower in comparison to M0, indicating increased shot-to-shot phase consistency between TD.

Discussion

We have confirmed our hypothesis that gradient moment nulling reduces shot-to-shot phase variation across averages. Strong shot-to-shot phase differences were observed along the z-axis, which corresponds to the direction of brain bulk motion apparent with other MRI techniques.2-4,14 With M0M1 and M0M1M2, we observed a reduction in the standard deviation of the shot-to-shot phase and increased consistency between TD times.

Typical brain DWI acquisitions are not synchronized to the cardiac cycle and thus variable motion induced phase is collected due to the timing corresponding to different TDs. If ECG gating is implemented such that data is collected at the TD that induces the minimum phase variation, the phase between shots may be more stable, but this cannot be accommodated for in multi-slice imaging. Motion compensation minimizes variable phase and thus the measured phase is more stable. This work demonstrates that M0M1 and M0M1M2 compensation can be used to stabilize the shot-to-shot phase without ECG gating. The removal of large phase variation should help with the reconstruction of images in challenging cases, such as highly accelerated multi-shot5-7 EPI or diffusion-prepared sequences.8

Conclusion

Diffusion encoding with velocity and/or acceleration compensated diffusion encoding gradients contributes to increased shot-to-shot phase consistency in brain DWI. We have demonstrated the feasibility and necessity of incorporating moment compensation for improved multi-shot DWI acquisitions.

Acknowledgements

We would like to acknowledge the following funding sources for supporting this ongoing work:

  • NIH R01 HL131823 to DBE
  • NIH R01 MH116173 to KS
  • NSF DGE-1656518 to AJH

References

  1. Enzmann DR, Pelc NJ. Brain motion: measurement with phase-contrast MR imaging. Radiology. 1992;185(3):653-660. doi:10.1148/radiology.185.3.1438741
  2. Pahlavian SH, Oshinski J, Zhong X, Loth F, Amini R. Regional Quantification of Brain Tissue Strain Using Displacement-Encoding With Stimulated Echoes Magnetic Resonance Imaging. J Biomech Eng. 2018;140(8):10.1115/1.4040227. doi:10.1115/1.4040227
  3. Terem I, Dang L, Champagne A, et al. 3D amplified MRI (aMRI). Magn Reson Med. 2021;86(3):1674-1686. doi:10.1002/mrm.28797
  4. Weaver JB, Pattison AJ, McGarry MD, et al. Brain mechanical property measurement using MRE with intrinsic activation. Phys Med Biol. 2012;57(22):7275-7287. doi:10.1088/0031-9155/57/22/7275
  5. Holdsworth SJ, O'Halloran R, Setsompop K. The quest for high spatial resolution diffusion-weighted imaging of the human brain in vivo. NMR Biomed. 2019;32(4):e4056. doi:10.1002/nbm.4056
  6. Hu Y, Wang X, Tian Q, et al. Multi-shot diffusion-weighted MRI reconstruction with magnitude-based spatial-angular locally low-rank regularization (SPA-LLR). Magn Reson Med. 2020;83(5):1596-1607. doi:10.1002/mrm.28025
  7. Madore B, Chiou JY, Chu R, Chao TC, Maier SE. Accelerated multi-shot diffusion imaging. Magn Reson Med. 2014;72(2):324-336. doi:10.1002/mrm.24919
  8. Gao Y, Zhou Z, Han F, Zhong X, Yang Y, Hu P. 3D isotropic resolution diffusion-prepared magnitude-stabilized bSSFP imaging with high geometric fidelity at 1.5 Tesla. Med Phys. 2020;47(8):3511-3519. doi:10.1002/mp.14195
  9. Aliotta E, Wu HH, Ennis DB. Convex optimized diffusion encoding (CODE) gradient waveforms for minimum echo time and bulk motion-compensated diffusion-weighted MRI. Magn Reson Med. 2017;77(2):717-729. doi:10.1002/mrm.26166
  10. Moulin K, Verzhbinsky IA, Maforo NG, Perotti LE, Ennis DB. Probing cardiomyocyte mobility with multi-phase cardiac diffusion tensor MRI. PLoS One. 2020;15(11):e0241996. Published 2020 Nov 12. doi:10.1371/journal.pone.0241996
  11. Szczepankiewicz F, Sjölund J, Dall'Armellina E, et al. Motion-compensated gradient waveforms for tensor-valued diffusion encoding by constrained numerical optimization. Magn Reson Med. 2021;85(4):2117-2126. doi:10.1002/mrm.28551.
  12. Stoeck CT, von Deuster C, Genet M, Atkinson D, Kozerke S. Second-order motion-compensated spin echo diffusion tensor imaging of the human heart. Magn Reson Med. 2016;75(4):1669-1676. doi:10.1002/mrm.25784
  13. Cork TE, Moulin K, Perotti LE, Middione MJ, Ennis DB. The Effects of Motion Compensated Encoding Waveforms in Cardiac Diffusion Tensor Imaging: A Moving Phantom Study. SCMR 24th Annual Meeting, 2021 (Virtual Meeting).
  14. Hannum AJ, McIlvain G, Sowinski D, McGarry MDJ, Johnson CL. Correlated noise in brain magnetic resonance elastography. Magn Reson Med. 2021;00:1-16. doi:10.1002/mrm.29050

Figures

Figure 1. (A) Average (Φavg) and (B) standard deviation of difference phase (σdiff) for one subject. Increased phase consistency between the minimum and maximum TD in M0M1M2 versus M0 and M0M1, particularly in the z diffusion direction. Variation of phase differences also reduced with the combined M0M1 and M0M1M2. Orange and blue boxes highlight phase stability and variance reduction in the z direction when evaluating M0 and M0M1M2, respectively.

Figure 2. A closer examination of Φavg and Φdiff for the TD with the (A) maximum variation and (B) minimum variation for the five acquired repetitions along the z diffusion direction in the central slice in one subject. We observe less extreme differences with M0M1 and M0M1M2. The Φavg and Φdiff for b=0 is provided for reference.

Figure 3. Phase differences between individual repetitions of a central brain slice for the TD with (A) maximum variation and (B) minimum variation for b=0 and the diffusion directions of one subject. We observe the greatest phase differences between repetitions for the z-axis diffusion encoding, particularly at the maximum TD (blue box). These differences are greatly reduced with the M0M1 and M0M1M2 gradient compensation (red box).

Figure 4. Standard deviation of phase across different brain slices for all subjects displayed as violin plots. Median phase per TD is indicated by the black line. The M0 acquisition shows that the density of the distribution has a longer spread closer to the tails, indicating more phase variation. The distribution narrows considerably across different TD for the M0M1M2 compensation, which indicates more phase consistency. The TD interval with the maximum (TD-1) and minimum phase (TD-7) variation are indicated by the blue and red boxes respectively.

Figure 5. Pearson’s correlation coefficient of Φavg between different TDs, averaged across all subjects for three slices. Phase is least correlated between TDs along the z-axis diffusion encoding direction (i.e. low/dark correlation for M0 encoding, but higher/brighter correlation for M0M1M2). This is improved with M0M1 and M0M1M2 compensation.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)
1625
DOI: https://doi.org/10.58530/2022/1625