1610
Fast 3D DCE MRI using partially separable model: autopilot Multitasking1UIH America, Inc., Houston, TX, United States, 2United Imaging Healthcare, Shanghai, China, 3Department of Radiology, Zhongshan Hospital, Fudan University, Shanghai, China, 4Department of Medical Imaging, Shanghai Medical College, Fudan University, Shanghai, China, 5Shanghai Institute of Medical Imaging, Shanghai, China
Synopsis
Inspired by Multitasking, we have developed a fast reconstruction method for 3D stack-of-star (SoS) acquisitions to achieve high temporal resolution (0.1s) DCE MRI without additional navigator data. The proposed method is fully compatible with existing sequence using 3D SoS trajectories, but with less computation complexity.
Introduction
Free-breathing DCE-MRI techniques combining compressed sensing (CS) and parallel imaging with golden-angle radial/spiral sampling have been developed to improve motion robustness with high spatial and temporal resolution [1-5]. These methods have demonstrated good diagnostic performance in clinical setting, but image quality will degrade at high acceleration rates and overall reconstruction time remains long. Multitasking [6, 7] is a technique that exploits low-rankness of images, captures - rather than avoids motion, relaxation and other dynamics to efficiently perform quantitative MRI without the use of ECG triggering or breath holds. Multitasking explicitly acquires navigator signal at high temporal-frequency, usually in the form of repeated readouts along a fixed orientation. We have implemented a fast recon method for 3D stack-of-star (SoS) acquisitions to achieve high temporal resolution DCE MRI using existing imaging protocol. Compared with Multitasking, the proposed method does not require sampling additional navigator data, making it compatible with existing GRE-3D-SoS sequences.Methods
The main goal of the proposed method is to recover the dynamic image sequence $$$\gamma( \textbf{x},t)$$$ from its under-sampled Fourier measurements acquired through multiple channels of a phased array coil, where $$$\textbf{x}$$$ and $$$\textit{t}$$$ represent space and time, respectively. We adopt the partially separable (PS) model [8-10] which assume $$$\gamma(\textbf{x},t)$$$ spatial-temporal partially separable. Then $$$\gamma(\textbf{x},t)$$$ can be represented as the product of a spatial coefficient matrix $$$U_s$$$ and a temporal basis $$$V_t$$$: $$$\Gamma^{M×N}=U_s^{M×R}\cdot V_t^{R×N}$$$, where $$\Gamma^{M×N}=\begin{pmatrix}\gamma(x_1,t_1)&\cdots&\gamma(x_1,t_N)\\\gamma(x_2,t_1) &\cdots&\gamma(x_2,t_N)\\\vdots&\ddots&\vdots\\\gamma(x_M,t_1)&\cdots& \gamma(x_M,t_N)\end{pmatrix}$$.Here, $$$\textit{M}$$$ is the number of voxels in the image and $$$\textit{N}$$$ is the number of image frames in the dataset. The columns of $$$\Gamma$$$ correspond to the voxels of each time frame. $$$\textit{R}$$$ is the order of the PS model, or rank of $$$\Gamma$$$.
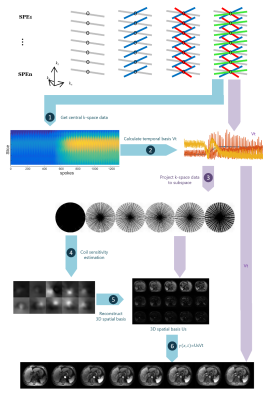
Flowchart of the image reconstruction pipeline is shown in Fig. 1. Step 1: Collect central k-space data from SoS trajectories; Step 2: Get temporal basis from the $$$R$$$ dominant right singular vectors through singular value decomposition (SVD) [8]; Step 3: Project all k-space data to a lower dimensional subspace; Step 4: Estimate 3D coil sensitivities from the first component of the projected data in subspace; Step 5: Calculate spatial coefficient matrix using coil sensitivities (from Step 4) and projected data (from Step 3); Step 6: Get motion resolved images from multiplication of spatial coefficient matrix (from Step 5) and temporal basis (from Step 2).
Results
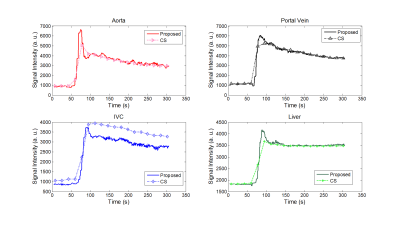
A 3D fast spoiled gradient echo SoS sequence with partial Fourier slice encoding was used for data acquisition. (TR/TE = 3.09/1.42 ms, FOV = 400mm2, slice thickness = 4mm, matrix size = 384 x 384 x 53, 20 channels). Consecutive spokes were rotated by 105.4 ͦ. For each spoke, a full set slice encoding (partially encoded) was acquired before moving to the next spoke. Fat saturation was used. Data was continually acquired for 5 minutes. In Fig. 2, the proposed (PS) method is compared with CS reconstruction using the same dataset. Top row shows three adjacent frames at t = 15.3s, 32.5s, 49.8s after bolus injection, from CS reconstruction. Breath motion suppression is added to CS reconstruction. Middle and bottom rows show PS reconstructed images at t = 19.22s, 30.64s, 33.18s, 36.09s, 38.35s, 41.71s after bolus injection, respectively. Because PS method achieves a higher temporal resolution, less motion artifacts is introduced (see lesions at yellow arrow). The distinctive microscopic anatomy of the spleen can be better observed in PS reconstructions.For CS reconstruction, k-space data was sorted into 18 phases thus each phase corresponded to 16.7s temporal resolution. For PS reconstruction, each spoke corresponded to whole 3D volume images in Step 6, and had a temporal resolution of 90ms. The temporal signal intensity curves of aorta, inferior vena cava (IVC), portal vein, and liver are shown in Fig. 3. PS method achieves high temporal resolution and maintains better signal temporal fidelity as reflected by steep rising and falling edges. A sharp bolus peak can be clearly observed in the PS method, whereas the peak is smoothed in CS reconstruction. In addition, a second bolus peak at 70s after the bolus injection can be seen from the PS reconstruction. The intensity curves suggest that the proposed method is superior to the state-of-the-art CS reconstruction methods in preserving kinetic information.
Conclusion and discussion
We have developed a novel approach using partially separable model for DCE imaging with ultra-high temporal resolution, without explicit acquisition of navigator signal. The approach effectively uses the existing CS imaging protocol, combines PS model, radial trajectory subspace projection in the same framework. The PS model can capture spatial-temporal correlation in non-adjacent dynamic image frames. As a result the PS model is able to preserve more temporal information, compared to CS reconstruction methods which use temporal total-variation sparse regularizations.Different from GRASP (as well as XD-GRASP, GRASPpro) [1-4], the proposed method does not sort k-space data into phases. As a result the computation complexity is far less than existing compressed sensing methods, making inline-reconstruction possible. The proposed method does not rely on golden angle, which makes sequence design more flexible. The proposed method can achieve 0.1s temporal resolution, without introducing spatial artifacts, allowing for quantitative assessment of liver perfusion characteristics. The proposed method was demonstrated to outperform existing methods in preserving kinetic information.
Acknowledgements
The authors thank beneficial discussion with Professor Debiao Li and Professor Anthony Christodoulou from the Biomedical Imaging Research Institute at Cedars-Sinai Medical Center.References
[1] Feng, Li, et al. "Golden‐angle radial sparse parallel MRI: combination of compressed sensing, parallel imaging, and golden‐angle radial sampling for fast and flexible dynamic volumetric MRI." Magnetic resonance in medicine 72.3 (2014): 707-717.
[2] Chandarana, Hersh, et al. "Free-breathing contrast-enhanced multiphase MRI of the liver using a combination of compressed sensing, parallel imaging, and golden-angle radial sampling." Investigative radiology 48.1 (2013).
[3] Feng, Li, et al. "XD‐GRASP: golden‐angle radial MRI with reconstruction of extra motion‐state dimensions using compressed sensing." Magnetic resonance in medicine 75.2 (2016): 775-788.
[4] Feng, Li, et al. "GRASP‐Pro: imProving GRASP DCE‐MRI through self‐calibrating subspace‐modeling and contrast phase automation." Magnetic resonance in medicine 83.1 (2020): 94-108.
[5] Lyu, Jingyuan, et al. “Highly accelerated 3D dynamic contrast enhanced MRI using partial separability model and JENSE”, pp.333, Proc. ISMRM (2014).
[6] Christodoulou, Anthony G., et al. "Magnetic resonance multitasking for motion-resolved quantitative cardiovascular imaging." Nature biomedical engineering 2.4 (2018): 215-226.
[7] Wang, Nan, et al. "Quantitative 3D dynamic contrast‐enhanced (DCE) MR imaging of carotid vessel wall by fast T1 mapping using Multitasking." Magnetic resonance in medicine 81.4 (2019): 2302-2314.
[8] Liang, Zhi-Pei. "Spatiotemporal imaging with partially separable functions." 2007 4th IEEE international symposium on biomedical imaging: from nano to macro. IEEE, 2007.
[9] Haldar, Justin P., and Zhi-Pei Liang. "Spatiotemporal imaging with partially separable functions: A matrix recovery approach." 2010 IEEE International Symposium on Biomedical Imaging: From Nano to Macro. IEEE, 2010.
[10] Zhao, Bo, et al. "Image reconstruction from highly undersampled (k, t)-space data with joint partial separability and sparsity constraints." IEEE transactions on medical imaging 31.9 (2012): 1809-1820.