1608
Joint reconstruction of multi-TE diffusion MRI acquired using TDM-EPI with complementary k-space sampling1Department of Psychiatry, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, United States, 2Wellcome Centre for Integrative Neuroimaging, FMRIB Division, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom, 3Department of Radiology, Stanford University, Stanford, CA, United States, 4Department of Radiology, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, United States, 5Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Harvard Medical School, Boston, MA, United States
Synopsis
Combined diffusion-relaxometry has demonstrated promising capability to noninvasively probe tissue microstructure by joint modeling of relaxation coefficients and diffusivity. Our recent work has introduced a sequence based on the time-division multiplexing technique to accelerate the acquisition of relaxation-diffusion MRI. In this work, we further developed the TDM-EPI sequence by integrating ky-shifted k-space sampling strategies for data acquired at different TEs. Moreover, we implemented and compared several reconstruction methods to integrate complementary k-space samples to joint estimate images at different TEs. The results showed that the joint reconstruction approach can improve image quality and reduce artifact compared with conventional reconstruction methods.
Introduction
Joint modeling of diffusion MRI (dMRI) with multiple echo-times (TEs), i.e., combined diffusion-relaxometry, has demonstrated promising capability to improve tissue microstructure estimation compared with standard single-TE dMRI1-5. However, the prolonged scan time and relative low SNR for dMRI with long TE are limitations for the application of the diffusion-relaxometry technique in neuroimaging research. To overcome the limitations, our recent work6 has introduced a time-division multiplexing echo-planar imaging (TDM-EPI) technique to accelerate the scan of diffusion-relaxometry, which can simultaneously acquire dMRI with multiple TEs to achieve ~3X acceleration while maintaining almost identical SNR and signal intensity compared with the standard method. In this work, we aim to further improve the image quality by combining novel acquisition schemes in TDM-EPI and advanced reconstruction algorithms. On the acquisition side, we introduce a modified TDM-EPI sequence with complementary k-space sampling, in which each echo has a relative Δ ky shift for k-space sampling. On the reconstruction side, we implement and compare different algorithms that jointly reconstruct multi-TE diffusion-weighted images by integrating complementary k-space samplings to improve the capability of parallel imaging.Methods
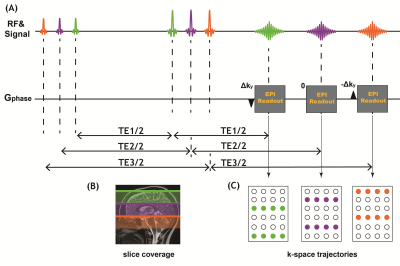
Data acquisition:Figure1 shows the proposed TDM-EPI sequence diagram where the relative shift of the k-space sampling along ky direction for the echoes at three different TE are +Δky ,0 and –Δky, respectively. The proposed sequence was implemented on a 3T MAGNETOM Prisma scanner to acquire multi-TE dMRI data from a healthy volunteer. To avoid double diffusion encoding effect7, echo-shifting gradient was applied adaptively perpendicular to the diffusion gradient and the shift factor kshift=9.1rad/mm following results from our previous work6. The scan parameters for the diffusion experiments were as follows: TR =3000ms, FOV=210×210mm2, PF=6/8, 2.0 mm isotropic resolution, TE = (79 ms, 109 ms and 139 ms). Diffusion-weighted images were acquired along 30 gradient directions at b = 500, 750, 1500, 2250, and 3000 s/mm2 together with 10 nondiffusion-weighted (b = 0 s/mm2) images.
Images reconstruction:
Joint GRAPPA methods:
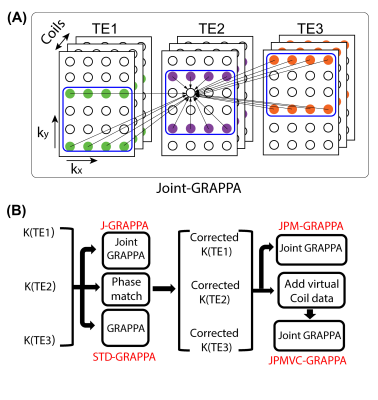
To exploit different sampling patterns across multi-TE, joint-GRAPPA was proposed for jointly reconstructing the multi-TE images8. The strategy of Joint-GRAPPA is illustrated in Figure 2A, in which the missing point are estimated not only from the nearby sampled points within the k-space but also from staggered points in other k-space with different TE. However, due to the shot-to-shot phase variations between the acquisitions with different TE, a joint reconstruction without a prior phase correction may cause ghosting artifact and signal cancelling. A phase-matching method (Figure 2B) was adopted for alleviating such artifacts from the phase inconsistent9. To further improve the performance of paralleling imaging, virtual coils concept is incorporated into the joint-GRAPPA reconstruction (Figure 2B).
Joint low-rank regularization methods:
The second set of methods exploit consistency between multi-contrast data using low-rank regularization following the MUSSELS method10,11. The MUSSELS method was initially used in multi-shot diffusion weighted imaging to effectively recovery artifact-free images from under-sampled data by generalizing the SENSE method. In this method, images are reconstructed as the solution to the following problem:
$$I_{t}=argmin\sum_t\parallel F_{t}CI_{t}-K_{t}\parallel_2^2+\lambda\parallel H(I_{t})\parallel_{*}$$
where t is the index of TE ,Ft is the undersampled Fourier operator, C is the coil sensitivity, It is the image-space data with the tth TE, Kt is the measured k-space data, and $$$\parallel H(I_{t})\parallel_{*}$$$is structured low-rank constraint. The virtual-coil based method (VC-MUSSELS) augments the image It with its complex conjugate, i.e.,$$$\left(\begin{array}{c}I_{t}\\ I_t^*\end{array}\right)$$$, in the low-rank regularization term9,12. The joint MUSSELS (J-MUSSELS) method uses the low-rank regularization for images at different TEs. The JVC-MUSSELS method uses the low-rank regularization for images from all three TEs and their complex conjugate.
Results
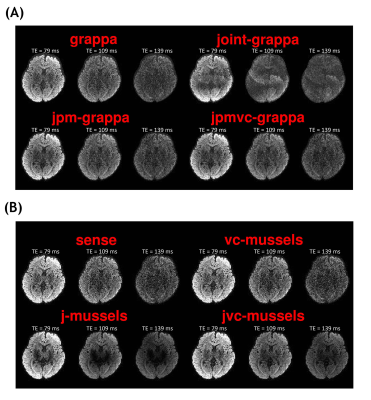
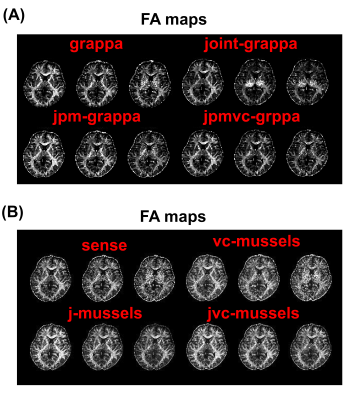
Figure 3A shows the diffusion weighted images of b=1000 s/mm2 at three different TEs from the standard GRAPPA and three generalized methods. Compared with the standard method, there are some significant ghosting artifacts and signal canceling in the images from J-GRAPPA method which are caused by inconsistent phases between measurements at different TEs. After the phase-matching procedure, the JPM-GRAPPA method successfully removed the ghosting artifact and improve the image quality. With the integration of the virtual-coil data, the JPMVC‐GRAPPA method further improved the image quality especially for the long-TE data. Figure 3B compares the images from standard SENSE, and the three low-rank regularization-based methods. The virtual-coil based method improved the image quality, especially at long TE, without using information from other TEs, which is consistent with results shown in12. Though the J-MUSSELS method also improves the image quality, it led to undesirable intensity loss at deep-brain regions, which may be related to sub-optimal regularization parameters. With the same parameter, the JVC-MUSSELS methods removed the intensity loss and further improved the image quality. Figure 4A and 4B compares the FA maps for the proposed methods. The FA measures from the JPM-GRAPPA and JVC-MUSSELS methods have less noise than other methods in the corresponding group.Discussion and Conclusion
We proposed a ky-shifted TDM-EPI with complementary k-space sampling in this study. To improve the images qualities, we performed and compared several reconstruction methods on the complementary k-space sampling dataset. The results show that our proposed method with the joint reconstruction obtained higher image quality, better SNR performance, and lower artifact level than conventional method.Acknowledgements
This study was supported in part by NIH grants R21MH116352, R21MH126396, K01MH117346, R01MH119222, R01MH116173, R01MH125860.References
1. Slator PJ, Palombo M, Miller KL, Westin CF, Laun F, Kim D, Haldar JP, Benjamini D, Lemberskiy G, de Almeida Martins JP. Combined diffusion‐relaxometry microstructure imaging: Current status and future prospects. Magn Reson Med 2021.
2. Kim D, Doyle EK, Wisnowski JL, Kim JH, Haldar JP. Diffusion‐relaxation correlation spectroscopic imaging: a multidimensional approach for probing microstructure. Magn Reson Med 2017;78(6):2236-2249.
3. Benjamini D, Basser PJ. Use of marginal distributions constrained optimization (MADCO) for accelerated 2D MRI relaxometry and diffusometry. J Magn Reson 2016;271:40-45.
4. Veraart J, Novikov DS, Fieremans E. TE dependent Diffusion Imaging (TEdDI) distinguishes between compartmental T2 relaxation times. Neuroimage 2018;182:360-369.
5. Gong T, Tong Q, He H, Sun Y, Zhong J, Zhang H. MTE-NODDI: Multi-TE NODDI for disentangling non-T2-weighted signal fractions from compartment-specific T2 relaxation times. Neuroimage 2020:116906.
6. Ji Y, Gagoski B, Hoge WS, Rathi Y, Ning L. Accelerated diffusion and relaxation‐diffusion MRI using time‐division multiplexing EPI. Magn Reson Med 2021. doi: 10.1002/mrm.28894.
7. Ji Y, Paulsen J, Zhou IY, Lu D, Machado P, Qiu B, Song YQ, Sun PZ. In vivo microscopic diffusional kurtosis imaging with symmetrized double diffusion encoding EPI. Magn Reson Med 2019;81(1):533-541.
8. Bilgic B, Kim TH, Liao C, Manhard MK, Wald LL, Haldar JP, Setsompop K. Improving parallel imaging by jointly reconstructing multi‐contrast data. Magn Reson Med 2018;80(2):619-632.
9. Liao C, Manhard MK, Bilgic B, Tian Q, Fan Q, Han S, Wang F, Park DJ, Witzel T, Zhong J. Phase-matched virtual coil reconstruction for highly accelerated diffusion echo-planar imaging. Neuroimage 2019;194:291-302.
10. Haldar JP. Low-rank modeling of local $ k $-space neighborhoods (LORAKS) for constrained MRI. IEEE Trans Med Imaging 2013;33(3):668-681.
11. Mani M, Jacob M, Kelley D, Magnotta V. Multi‐shot sensitivity‐encoded diffusion data recovery using structured low‐rank matrix completion (MUSSELS). Magn Reson Med 2017;78(2):494-507.
12. Bilgic B, Liao C, Manhard MK, Tian Q, Chatnuntawech I, Iyer SS, Cauley SF, Feiweier T, Giri S, Hu Y. Robust high-quality multi-shot EPI with low-rank prior and machine learning. 2019.
Figures