1606
A Locally Structured Low-Rank Tensor Method Using Submatrix Constraints for Joint Multi-echo Image Reconstruction1Wellcome Centre for Integrative Neuroimaging, FMRIB, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom
Synopsis
Recently, we proposed an improved structured low-rank (SLR) reconstruction - locally structured low-rank (LSLR) method, which forces low-rank constraints on submatrices of the Hankel structured matrix. This simple modification leads to a robust improvement over conventional SLR reconstruction, which has been validated on the low-rank tensor reconstruction for the multi-echo GRE data.
Introduction
Structured low-rank (SLR) methods have been used in a variety of MR image reconstruction problems, and offer great flexibility to exploit the intrinsic linear dependency in single channel images1, or across multiple channels/shots/contrasts of MR data2-6. SLR methods formulate this linear dependency in MR data as the low-rank property of a structured Hankel matrix generated from k-space data. These methods have also been extended to multi-dimensional structured tensor problems6,7. While conventional SLR methods enforce the low-rank constraint on the entire structured matrix, we recently proposed the Locally Structured Low-rank method (LSLR), which relaxes the low-rank constraint by enforcing it on submatrices of the Hankel structured matrix. Here we extend the LSLR method to structured low-rank tensor reconstruction, and demonstrate its benefit over conventional SLR approaches on a calibration-less, multi-echo joint reconstruction of retrospectively under-sampled GRE data.Methods
The LSLR method is demonstrated here for a calibration-less multi-echo joint tensor reconstruction using a non-convex formulation:$$\widehat{X}=argmin\left \| EX-Y \right \|^{2}\\s.t. rank(\Gamma _iH_1X)=r_1,\forall {\Gamma _i}\in\Omega _1 \\ ~~~~~ rank(\Gamma_jH_2X)=r_2,\forall {\Gamma _j}\in\Omega _2$$
Where $$$X\in\mathbb{C} ^{n^2 \times N_c \times N_e}$$$ corresponds to the k-space data of a $$$n \times n$$$ image with $$$N_c$$$ channels and $$$N_e$$$ echoes. $$$Y\in\mathbb{C} ^{N_k\times N_c\times N_e}$$$denotes the sampled data and E represents the sampling operator. We define an underlying Hankel transform operator for multi-coil data with a $$$n \times n$$$ patch size as $$$H:\mathbb{C} ^{n^2 \times N_c}\rightarrow \mathbb{C} ^{l\times d^2 N_c}$$$ where $$$l=(n-d+1)^2$$$, and a low-rank tensor $$$\mathbb{C} ^{l\times d^2 N_c \times N_e}$$$ can be constructed using an additional echo dimension. The operator $$$H_1:\mathbb{C} ^{n^2 \times N_c \times N_e}\rightarrow \mathbb{C} ^{l\times d^2 N_c N_e}$$$ concatenates the Hankel matrix representation of each echo across the column (channel) dimension, and $$$H_2:\mathbb{C} ^{n^2\times N_c \times N_e}\rightarrow \mathbb{C} ^{lN_e\times d^2 N_c}$$$concatenates them along the row (patch) dimension, so $$$H_1X$$$ and $$$H_2X$$$ correspond to the one-mode and two-mode unfolding matrices of the low-rank tensor as defined in6. $$$r_1$$$ and $$$r_2$$$ are two rank parameters, and $$$\Gamma _i$$$ and $$$\Gamma _j$$$ are submatrix selection operators (see Fig.1). $$$\Gamma _i:\mathbb{C} ^{l \times d^2N_cN_e}\rightarrow \mathbb{C} ^{s \times d^2N_cN_e}$$$selects a submatrix of $$$s$$$ consecutive rows from $$$H_1X$$$ . Similarly, $$$\Gamma _j:\mathbb{C} ^{l N_e \times d^2N_c}\rightarrow \mathbb{C} ^{s \times d^2N_c}$$$selects a submatrix of $$$s/N_e$$$ consecutive rows from the Hankel matrix of each echo (same relative position) and horizontally concatenate them together. $$$\Omega _1$$$ is the partition consisting of all possible $$$\Gamma _i$$$-selecting non-overlapping submatrices of $$$H_1X$$$, and similarly for $$$\Omega _2$$$ with $$$\Gamma _j$$$ and $$$H_2X$$$. As the Hankel structured matrix $$$H_*X$$$ is assumed to be low-rank in conventional SLR reconstructions, each submatrix should also be low-rank. The optimization was solved by ADMM8. To avoid boundary artifacts, the submatrices were randomly shifted every iteration9.
A GRE dataset with 8 compressed channels and 2 echoes was retrospectively under-sampled. Three different under-sampling patterns were explored (4 extra central lines were always sampled and complementary sampling was used for two echoes): 1) “Uniform sampling”: uniformly sampled readout lines for each echo (R=4); 2) “PF sampling”: an additional 3/4 PF sampling was applied on each echo10; 3) “Random sampling”: randomly sampled readout lines for each echo (R=4). A single echo reconstruction and three separate multi-echo joint reconstructions were performed by enforcing the low rank property on the one-mode unfolding matrix only, on the two-mode unfolding matrix only and on both unfolding matrices simultaneously. The virtual conjugate coils approach (VC)11 was also incorporated for PF and randomly sampled data. The kernel size of Hankel transform was $$$5 \times 5$$$ . A maximum of 1500 iterations was used for the uniform and PF sampling, and 2500 iterations for the random sampling due to slower convergence. Rank parameters were optimized for each SLR reconstruction. The number of submatrices $$$m$$$ used for LSLR is specified as in LSLR($$$m$$$). Normalized Root Mean Square Error (NRMSE) was calculated by using the fully-sampled data as reference.
Results
Figure 2 shows the single echo reconstruction for the first echo by SLR and LSLR. We compare SLR and LSLR across a variety of rank parameters, where all LSLR(2) reconstructions converge to a lower NRMSE than SLR at the same rank, at the cost of slower convergence. LSLR(4) reconstructions converge to a comparable NRMSE to LSLR(2) but requiring more iterations, except at r=80 where it had not yet converged at the maximum iteration. Figure 3 shows the multi-echo joint reconstruction results of the uniform sampled data, highlighting improved NRMSE for LSLR compared to SLR for each unfolding and in the tensor formulation ("both"). Figures 4 and 5 show the tensor reconstruction results of the PF sampled data and randomly sampled data respectively, indicating reduced NRMSE compared to conventional SLR constraint in both cases.Conclusion
In contrast to conventional SLR reconstruction, the proposed LSLR enforces low-rank constraints on submatrices of the structured low-rank matrix or unfolding matrices of the low-rank tensor. This simple modification leads to a robust improvement over conventional SLR reconstruction, which is validated across a variety of low-rank reconstruction formulations. LSLR(2) is a good choice balancing reconstruction performance and computational efficiency. Although the optimal number of submatrices is data-dependent, a relatively small number (e.g. 2/4/6) is sufficient to achieve consistent improvements in our preliminary experience.Acknowledgements
The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z). MC and WW are supported by the Royal Academy of Engineering (RF201617\16\23, RF201819\18\92). MC also receives research support from Engineering and Physical Sciences Research Council (EP/T013133/1).References
1. Haldar, J.P., Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI. IEEE Trans Med Imaging, 2014. 33(3): p. 668-81.2. Shin, P.J., et al., Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn Reson Med, 2014. 72(4): p. 959-70.
3. Haldar, J.P. and J. Zhuo, P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data. Magn Reson Med, 2016. 75(4): p. 1499-514.
4. Bilgic, B., et al., Improving parallel imaging by jointly reconstructing multi‐contrast data. Magnetic resonance in medicine, 2018. 80(2): p. 619-632.
5. Mani, M., et al., Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS). Magn Reson Med, 2017. 78(2): p. 494-507.
6. Yi, Z., et al., Joint calibrationless reconstruction of highly undersampled multicontrast MR datasets using a low-rank Hankel tensor completion framework. Magn Reson Med, 2021. 85(6): p. 3256-3271.
7. Hess, A.T., I. Dragonu, and M. Chiew, Accelerated calibrationless parallel transmit mapping using joint transmit and receive low-rank tensor completion. Magn Reson Med, 2021.
8. Boyd, S., Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Foundations and Trends® in Machine Learning, 2010. 3(1): p. 1-122.
9. Saucedo, A., et al., Improved computational efficiency of locally low rank MRI reconstruction using iterative random patch adjustments. IEEE transactions on medical imaging, 2017. 36(6): p. 1209-1220.
10. Koopmans, P.J. and V. Pfaffenrot, Enhanced POCS reconstruction for partial Fourier imaging in multi‐echo and time‐series acquisitions. Magnetic Resonance in Medicine, 2021. 85(1): p. 140-151.
11. Bilgic, B., et al. Robust high-quality multi-shot EPI with low-rank prior and machine learning. in Proc Int Soc Magn Reson Med. 2019.
Figures
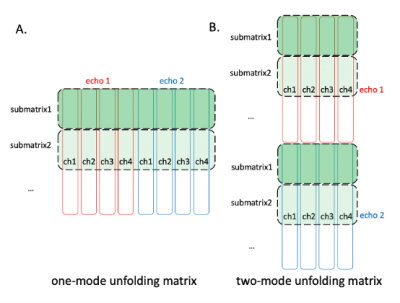
Figure 1. An example of submatrix construction on different unfolding matrices of the low-rank tensor generated from a 4-channel, 2-echo k-space. Each long block corresponds to the Hankel matrix of a single channel. A. For the one-mode unfolding matrix which treats different echoes as virtual channels, each submatrix consists of a subset of consecutive rows. B. For the two-mode unfolding matrix which treats different echoes as virtual patches, each submatrix consists of two subsets of consecutive rows corresponding to k-space patches from two echoes at the same location.
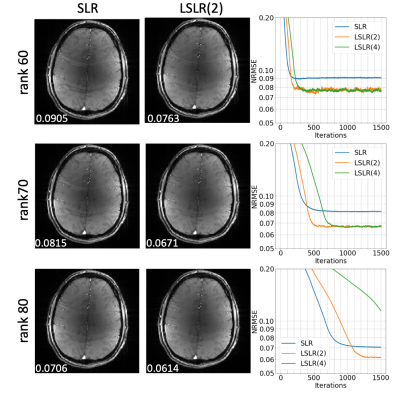
Figure 2. The results of single echo reconstruction for the first echo of uniformly sampled data. The reconstructed images of SLR and LSLR(2) at r=60 (top), r=70 (middle), and r=80 (bottom) are shown. NRMSE calculated for two echoes together are shown in the figure. Note LSLR(4) at r=80 had not converged within the maximum 1500 iterations.
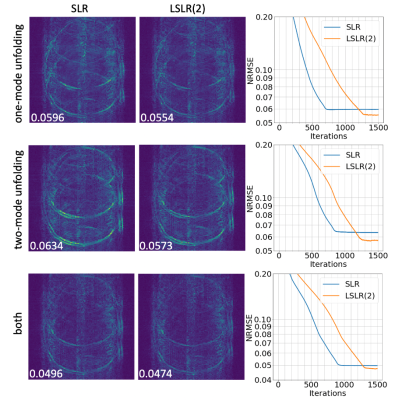
Figure 3. The results of three separate multi-echo joint reconstructions for the uniformly sampled data. Top: “one-mode unfolding. Middle: “two-mode unfolding”. Bottom: “both”. The difference between the reconstructed image and the reference image of SLR and LSLR(2) is shown on the left for the first echo. NRMSE values calculated for two echoes are shown in the figure.
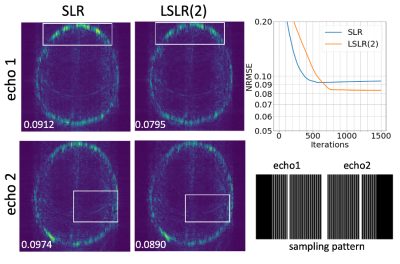
Figure 4. The results of multi-echo joint low-rank tensor reconstruction using both two modes unfolding matrices with VC for the PF sampled data. The difference between the reconstructed image and the reference image of SLR and LSLR(2) is shown on the left for echo1 (top) and echo2 (bottom). Subtle differences between SLR and LSLR(2) can be observed within the white box. NRMSE values calculated for each echo exclusively are shown in the figure respectively.
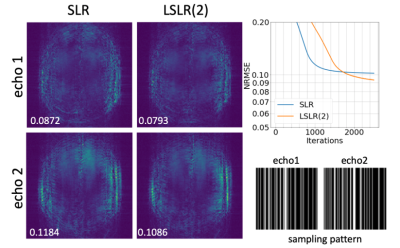
Figure 5. The results of multi-echo joint low-rank tensor reconstruction using both two modes unfolding matrices with VC for the randomly sampled data. The difference between the reconstructed image and the reference image of SLR and LSLR(2) is shown on the left for echo1 (top) and echo2 (bottom). NRMSE values calculated for each echo exclusively are shown in the figure respectively.