INTRODUCTION

GRASP as an iterative image reconstruction algorithm for dynamic contrast-enhanced MRI, incorporates L1-type regularization seeking temporal correlation and sparsity along the time domain to supress undersampling artifacts. This type of regularization is universal, doesn’t have a closed form solution with a high computational cost. We propose to use a subject-specific data-driven L2-type regularization generated from low-resolution images to replace the current GRASP regularization. This potentially can improve image quality and address the computational cost since L2 term is differentiable and computationally more tractable than L1.

METHODS

Data acquisition: Free-breathing 3D abdominal imaging was performed on seventeen cancer patients with contrast injection on a 3T scanner (Signa Premier, GE Healthcare, Waukesha, WI). A product T1-weighted golden-angle stack-of-stars pulse sequence (DISCO STAR) was used with the following acquisition parameters: repetition time/echo time (TR/TE) = 4/1.9 ms, field of view (FOV) = 320×320×140 mm³ , number of readout points in each spoke = 480, flip angle= 12 °, pixel bandwidth= 244 Hz and spatial resolution =1.6×1.6×5 mm³. A total of 1400 spokes were acquired, with a total scan time of approximately three minutes. GRASP reconstruction: 900 spokes with 20 temporal frames (45 spokes in each frame) were generated by sorting the continuously acquired data [1] and iterative GRASP reconstruction was performed to solve the following minimization [1]:
$$d = argmin ||FCd-m||_2+α||Gd||_1$$
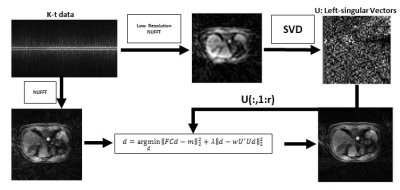
where F is non-uniform fast Fourier transform (NUFFT), C is the n-element coil sensitivity maps, m is the multi-coil (c coils) radial data sorted into t temporal phases, d is the reconstructed time-resolved images, G is the temporal difference transform along the time dimension, and α=0.03 as a regularization parameter. EigenGRASP reconstruction: For a desired slice, k-t data for five slices above and below were selected (to increase the training data and select similar anatomies). NUFFT reconstruction was performed by choosing only the center of k-space (70 read-out points) and low-resolution images with the same number of phases as GRASP reconstruction were generated. Images were collapsed into a two-dimensional matrix (voxel, phase) and SVD was performed. Left-singular vectors (U) were selected, truncated (r=7) and the cost function shown in Figure 1 was minimized. w is a weighting mask with lower values on voxels with the largest signal (i.e. aorta) along time. λ=5 was chosen as the regularization parameter.

RESULTS

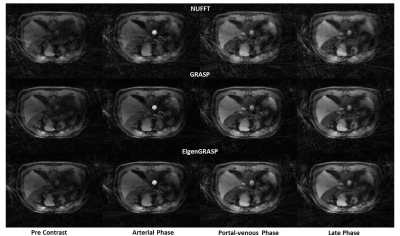
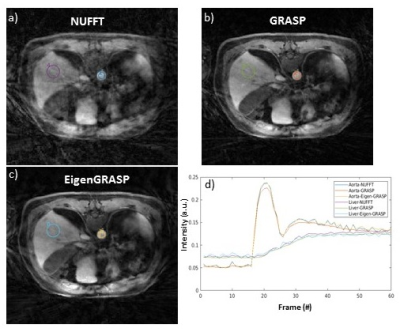
Figure 2 compares NUFFT (top) and GRASP (middle) reconstruction, with the proposed EigenGRASP (bottom) results. Both GRASP and EigenGRASP show good contrast agreement in the liver, aorta, muscle and fat tissues. While GRASP preserves more imaging details (middle, Portal-venous phase) compared to EigenGrasp recon, the latter (bottom-portal-venous phase) is more successful in suppressing artifacts. ROI analysis in Figure 3 comparing contrast dynamics in the aorta and liver shows good agreement among the three (NUFFT, GRASP, EigenGRASP) reconstructions. The contrast curves in the GRASP reconstruction are smoother compared to EigenGRASP. However, in aorta region the peak is smaller in GRASP compared to NUFFT reconstruction while EigenGRASP has a more similar peak suggesting a better preservation of the contrast.

CONCLUSION

The proposed EigenGRASP with the use of temporal learning generated images with a similar quality to the ones in GRASP. Compared to other eigen-based learning methods [2,3] including GRASP-PRO where low-resolution GRASP images are used for training, we only use NUFFT results (computationally efficient) and L1 term is replaced with a new L2 term minimization. Although we used the same iterative optimization solver and stopping criteria for both GRASP and EigenGRASP, in theory the EigenGRASP with a closed form solution can be directly solved which would decrease the computation cost. This study has a number of limitations including the number of training cases and a more systematic way of selecting SVD truncation and optimization parameters is desired.

Acknowledgements

No acknowledgement found.