1604
Rapid CS-Wave MPRAGE acquisition with automated parameter selection1Centre for Functional and Metabolic Mapping (CFMM) | Robarts Research Institute | Western University, London, ON, Canada, 2Department of Medical Biophysics | Schulich School of Medicine and Dentistry | Western University, London, ON, Canada, 3Department of Radiology | Athinoula A. Martinos Center for Biomedical imaging | Massachusetts General Hospital & Harvard Medical School, Charlestown, MA, United States, 4Siemens Medical Solutions USA, Inc., Charlestown, MA, United States, 5Department of Radiology | Harvard Medical School, Boston, MA, United States, 6Fetal-Neonatal Neuroimaging & Developmental Science Center | Boston Children's Hospital, Boston, MA, United States, 7Harvard-MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA, United States
Synopsis
Wave encoding mitigates g-factor noise amplification in highly accelerated parallel imaging but achieving ultra-high acceleration factors is precluded by the intrinsic “√R” SNR penalty. To overcome this limitation, we propose a compressed sensing-based reconstruction with automatic selection of the regularization weighting. Moreover, we show that CS-Wave is flexible enough to perform well with uniform undersampling. We compare reconstruction performance of CS-Wave against the state-of-art Wave-LORAKS which requires parameter tuning, and evaluate different undersampling patterns at R=12-fold acceleration. Results indicate higher reconstruction quality and showcase the feasibility of ultra-fast Wave-MPRAGE acquisitions.
Introduction
Wave encoding1 enables highly accelerated parallel imaging2–4 using a corkscrew sampling trajectory to take full advantage of the 3D coil sensitivity distribution and provides reconstructions with minimum artifacts and negligible g-factor5 penalty. While its deployment in the MPRAGE sequence allowed for R=9-fold acceleration with adequate quality6,7, pushing the speed further is precluded by the intrinsic “$$$\sqrt{R}$$$” penalty, as well as the reduced SNR inherent in the inversion recovery preparation and train of low flip angle excitations. Regularized reconstructions in the form of CS-Wave8 and Wave-LORAKS9 provide an effective way to combat low SNR and push the acceleration to R=12-fold or higher, while matching the fidelity of unregularized wave-CAIPI.An important limitation of both CS-Wave and Wave-LORAKS is the need for appropriate selection of the regularization weighting. To circumvent time-consuming manual tuning, a novel CS reconstruction with automatic parameter selection was recently presented10. In this work, we extend this approach to wave encoding, compare its performance to the state-of-the-art Wave-LORAKS at 12-fold acceleration, and evaluate different undersampling patterns.
Methods
AcquisitionRetrospective Acceleration
Cartesian fully sampled MPRAGE data were acquired using a 3T system (Skyra, Siemens) with 32 receiver coils. Sequence parameters were 1mm isotropic resolution, FOV of 256x256x192 mm, and TE/TI/TR = 3.49/1100/2500 ms. From the fully sampled acquisition, wave encoding was simulated with sinusoidal wave gradients Gy,z of 8 mT/m, and 15 cycles. Data were then retrospectively undersampled using uniform and Poisson11,12 patterns to achieve 12-fold acceleration.
Prospective Acceleration
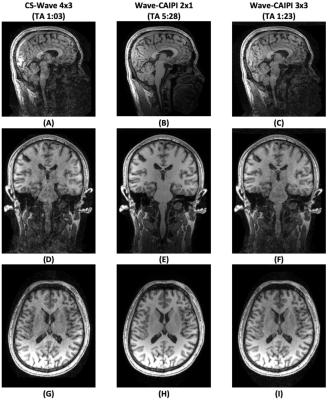
We replicated the previous sequence parameters to acquire Wave-MPRAGE data using 2x1, 3x3 and 4x3 uniform undersampling (5:28, 1:23 and 1:03 acquisition times, respectively). Sinusoidal wave gradients were with Gy,z of 10 mT/m, and 13 cycles.
For both retrospective and prospective acquisitions an external GRE reference scan was used to estimate sensitivity coil maps with ESPIRIT13.
Reconstruction
Standard Wave-CAIPI reconstruction minimizes1,
$$\hat{x}=\textrm{argmin}_x\hspace{1mm}\|Ax-y\|_2^2,\hspace{3mm}\textrm{(1)}$$
where $$$x$$$ is the unknown image, $$$y$$$ are the acquired data, and $$$A=SF_{jk}PF_{i}C$$$ is the forward model. This forward model is composed of sensitivity profiles, $$$C$$$, a Fourier transform in the frequency-encoding direction, $$$F_i$$$, wave point-spread-function, $$$P$$$, a Fourier transform in phase- and partition-encoding directions, $$$F_{jk}$$$, and the undersampling operator, $$$S$$$.
To improve the reconstruction, Wave-LORAKS includes a regularizer that promotes support, smooth phase, and parallel imaging constraints simultaneously (S-based LORAKS formulation14),
$$\hat{x}=\textrm{argmin}_x\hspace{1mm}\|Ax-y\|_2^2+\lambda J(P(x)),\hspace{3mm}\textrm{(2)} $$
where $$$P(*)$$$ constructs a structured matrix out of the data for those constraints, and $$$J(*)$$$ is the cost function that penalizes matrices with large rank. Wave-LORAKS requires tuning the radius of the LORAKS kernel, the rank for the S-matrix, and the regularization weighting, $$$\lambda$$$9.
The proposed CS-Wave includes a regularizer that promotes sparsity,
$$ \hat{x} = \textrm{argmin}_x\hspace{1mm}\| Ax - y \|_2^2+\lambda_{\textrm{auto}}\|\Psi x\|_1,\hspace{3mm}\textrm{(3)}$$
with a novel method to automatically select the regularization weighting, $$$\lambda_{\textrm{auto}}$$$, which determines the regularization weighting for each decomposition level, $$$L$$$, of the wavelet transform, $$$W$$$10. This method determines each $$$\lambda$$$ as the boundary between two clusters composed by signal-based and noise-based wavelet coefficients from the wavelet transform of the zero-filled reconstruction10.
Results
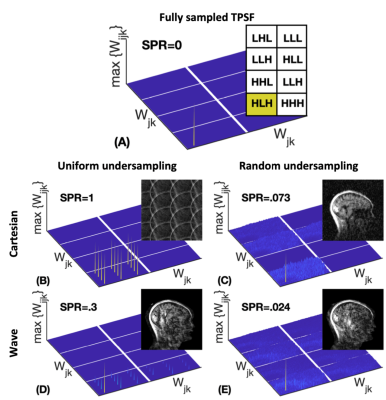
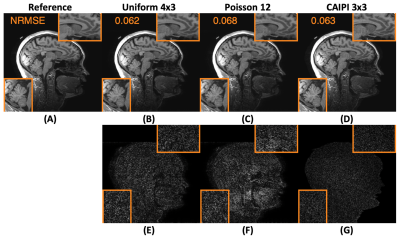
Figure 1 shows how wave encoding generates incoherence on its own for CS-Wave and does not require an undersampling pattern. This is important as transforming aliasing into noise-like artifacts from the zero-filled reconstruction allows the determination of $$$\lambda_{\textrm{auto}}$$$. The transform point spread function (TPSF)12, $$$WA^{-1}AW^{-1}\delta_{\textrm{HLH}}$$$, was used to analyze this interaction between wave encoding and the undersampling patterns, and their effect on compressed sensing-based reconstruction11. Here, $$$\delta_{\textrm{HLH}}$$$ denotes a delta function randomly located in a region for high-frequency wavelet coefficients in two dimensions mixed with one low-frequency wavelet coefficients in the third dimension.Figure 2 shows that CS-Wave reconstruction from uniform sampling provides better performance than Poisson undersampling (6.2% vs 6.8% NRMSE). Furthermore, CS-Wave is as good as Wave-CAIPI at 9-fold acceleration (6.2% vs 6.3% NRMSE).
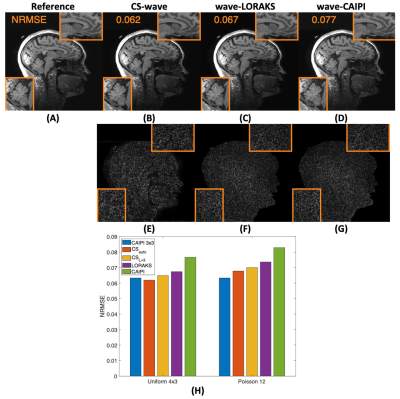
Figure 3 shows the comparison between CS-Wave, Wave-LORAKS and wave-CAIPI reconstructions for uniform undersampling at 12-fold acceleration. From the reconstructions and the error maps, Wave-LORAKS and -CAIPI are noisier than CS-Wave, which is reflected in the NRMSE values. Panel (H) shows reconstruction performance that favors CS-Wave with automatic selection of the decomposition level over the other methods.Figure 4 compares CS-Wave with 4x3 uniform sampling to Wave-CAIPI with uniform 3x3 and 2x1. There is high similarity between Wave-CAIPI at 9-fold acceleration with CS-Wave at 12-fold acceleration.
Discussion and Conclusion
In this work, we proposed a CS-Wave reconstruction with automated parameter selection, and showed that this provides improved reconstruction performance over wave-CAIPI as well as the state-of-the-art wave-LORAKS. Moreover, we systematically compared results to Wave-CAIPI at 9-fold acceleration for been clinically adequate6,7. Compared to wave-LORAKS which has 3 parameters that need to be determined, the proposed CS-Wave does not need parameter tuning. Through TPSF analysis and NRMSE calculation in retrospective reconstructions, we have shown that wave encoding provides the desired incoherence for CS-Wave parameter estimation and reconstruction to work well even with uniform undersampling, thus obviating the need for random sampling that would complicate sequence design. Our conclusion is that Wave encoding with uniform sampling and novel parameter-free CS-Wave reconstruction provides images on the same level as clinically validated Wave-MPRAGE.Acknowledgements
This project was supported by a Canadian Institutes of Health Research (CIHR) grant FRN 148453 and NSERC Discovery grant to R.S.M.; and BrainsCAN, the Canada First Research Excellence Fund award to Western University. This work was also supported by research grants NIH R01 EB028797, R03 EB031175, U01 EB025162, P41 EB030006, U01 EB026996, and the NVidia Corporation for computing support. GVM wants to thank the support of ISMRM through the 2021 Research Exchange Program grant. Finally, authors want to thank Siemens for the Wave-MPRAGE WIP 1084c sequence used in this work.References
1. Bilgic, B. et al. Wave‐CAIPI for highly accelerated 3D imaging. Magnet Reson Med 73, 2152–2162 (2015).
2. Griswold, M. A. et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magnet Reson Med 47, 1202–1210 (2002).
3. Pruessmann, K. P., Weiger, M., Scheidegger, M. B. & Boesiger, P. SENSE: Sensitivity encoding for fast MRI. Magnet Reson Med 42, 952–962 (1999).
4. Feinberg, D. A. & Setsompop, K. Ultra-fast MRI of the human brain with simultaneous multi-slice imaging. J Magn Reson 229, 90–100 (2013).
5. Larkman, D. J. Parallel Imaging in Clinical MR Applications. Medical Radiology 37–48 (2007) doi:10.1007/978-3-540-68879-2_3.
6. Polak, D. et al. Wave‐CAIPI for highly accelerated MP‐RAGE imaging. Magnet Reson Med 79, 401–406 (2018).
7. Longo, M. G. F. et al. Evaluation of Ultrafast Wave-CAIPI MPRAGE for Visual Grading and Automated Measurement of Brain Tissue Volume. Am J Neuroradiol 41, 1388–1396 (2020).
8. Bilgic, B., Ye, H., Wald, L. L. & Setsompop, K. Simultaneous Time Interleaved MultiSlice (STIMS) for Rapid Susceptibility Weighted acquisition. Neuroimage 155, 577–586 (2017).
9. Kim, T. H., Bilgic, B., Polak, D., Setsompop, K. & Haldar, J. P. Wave‐LORAKS: Combining wave encoding with structured low‐rank matrix modeling for more highly accelerated 3D imaging. Magnet Reson Med 81, 1620–1633 (2019).
10. Varela‐Mattatall, G., Baron, C. A. & Menon, R. S. Automatic determination of the regularization weighting for wavelet‐based compressed sensing MRI reconstructions. Magnet Reson Med 86, 1403–1419 (2021).
11. Ong, F., Cheng, J. Y. & Lustig, M. General phase regularized reconstruction using phase cycling. Magnet Reson Med 80, 112–125 (2018).
12. Lustig, M., Donoho, D. & Pauly, J. M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnet Reson Med 58, 1182–1195 (2007).
13. Uecker, M. et al. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magnet Reson Med 71, 990–1001 (2014).
14. Haldar, J. P. Low-Rank Modeling of Local k-Space Neighborhoods (LORAKS) for Constrained MRI. Ieee T Med Imaging 33, 668–681 (2014).
Figures