1563
Non-selective refocusing pulse optimization for T2-prep in free-breathing 3D CMRA at 7T with single-transmit coil
Shubhajit Paul1, Raphael Tomi-Tricot1,2, Karl Philipp Kunze1,2, Shaihan Malik1,3, Joseph V. Hajnal1,3, Philippa Bridgen1,3, Thomas Wilkinson1,3, Sharon Giles1,3, Radhouene Neji1,2, Reza Razavi1, Claudia Prieto1,4, and René Michael Botnar1,4
1School of Biomedical Engineering and Imaging Sciences, King’s College London, London, United Kingdom, 2MR Research Collaborations, Siemens Healthcare Limited, Frimley, United Kingdom, 3The London Collaborative Ultra high field System (LoCUS), London, United Kingdom, 4Escuela de Ingeniería, Pontificia Universidad Católica de Chile, Santiago, Chile
1School of Biomedical Engineering and Imaging Sciences, King’s College London, London, United Kingdom, 2MR Research Collaborations, Siemens Healthcare Limited, Frimley, United Kingdom, 3The London Collaborative Ultra high field System (LoCUS), London, United Kingdom, 4Escuela de Ingeniería, Pontificia Universidad Católica de Chile, Santiago, Chile
Synopsis
In spite of the promised increase in signal-to-noise ratio and contrast to noise ratio, 3D whole-heart imaging at 7T remains challenging predominantly due to B1, B0 inhomogeneity, specific absorption rate limitations and coil-depth issues for single transmit. Here, we developed a toolbox to optimize the adiabatic hyperbolic secant refocusing pulse with respect to B1 and B0 inhomogeneity typically used for T2-preparation in non-contrast 3D Coronary Magnetic Resonance Angiography (CMRA). We present phantom and in vivo data for 3D CMRA employing a low excitation flip-angle scheme.
INTRODUCTION:
MRI has become a reference standard for the assessment of cardiac disease due to its excellent soft-tissue contrast. To utilize the increased signal-to-noise ratio (SNR) and contrast-to-noise ratio (CNR) at ultra-high field strength (7T), development of new cardiac imaging techniques is necessary surpassing the limitations imposed by magnetic-field inhomogeneity, SAR constraints and also the coil-depth1 issues of surface-coils.2–6 The increased transmit field (B1+) heterogeneity in the body at 7T leads to an inhomogeneous flip angle (FA) distribution including regions of complete signal cancelation within the volume of interest6,7. So far only a few 3D Coronary Magnetic Resonance Angiography (CMRA) studies at 7T were reported2,4 employing thin slabs (without whole-heart coverage) using two channel quadrature surface-coils.For non-contrast enhanced CMRA, T2-preparation is used to improve the contrast between the coronary arteries and myocardium. To our best knowledge, no numerical optimization method has been proposed for T2-preparation refocusing pulses in cardiovascular imaging. We therefore sought to develop an optimization toolbox for the adiabatic hyperbolic secant (HS) pulse used in T2-preperation (T2-prep). We incorporated the T2-prep in a free-breathing 3D dual-echo CMRA pulse-sequence (Figure 1) for imaging a 7T. The T2-prepared CMRA sequence has been validated in phantom and healthy subjects employing a low-excitation flip-angle scheme.
METHODS:
1. Pulse optimization toolbox:The pulse optimization toolbox (Figure 2) is written in MATLAB (v9.4, The MathWorks, Massachusetts, USA) and consists of the following four modules: Bloch simulation tool, numerical optimization tool for RF pulses, numerical simulation of the optimized pulse performance, RF pulse-shape generator for Siemens scanners. The actual rotation angle provided by a RF refocusing pulse with nominal flip angle (α) of π radians can be represented as α. B1ratio . Here is the ratio of effective field to the nominal RF field strength. All optimizations were carried out on discrete grids of B1ratio and ΔB0 values with respective ranges of [0.2, 1.5] and ±500 Hz.
HS pulses10,11 with the following pulse-profile variant were used
B1 (t)=A(t)eiϕ(t)
with amplitude modulation:
A(t)=A0 sech(βt) ---(1)
and phase modulation:
ϕ(t)=µln[sech(βt) ]+ µln(A0)
Where A0 is the peak B1 amplitude, µ and β control the shape of the amplitude and phase modulation functions and therefore are optimized.
3D Bloch-simulation tool: was written to efficiently handle pulse profiles and generate the magnetization components (Mx, My, Mz) separately.
Numerical optimization of the HS pulse: was performed for the optimal suppression of the human myocardium using the 8Tx/16Rx surface-coil from Rapid (Rapid Biomedical GmbH, Rimpar, Germany) in single-transmit (1Tx) mode for 7T using the abovementioned optimization grid. The numerical optimizations and simulations were performed in a cartesian magnetization space (Mx, My, Mz).8 To obtain the optimum inversion from the HS pulse we solved a minimization problem utilizing the interior-point algorithm to minimize the cost function
f = 1/(p.q) ∑(i,j=1)(p,q) (1/(B1ratio)i,j ) . | Mx,ij + My,ij | ---(2)
with the following patient and hardware safety constraints
Pl ≤ Vmax
A0 ≤ (B1)max
SAR ≤ (SAR)10g,max
with
SAR = (1/T) . (σ/ρ) ∫0T |A(t)|2 dt
here Vmax is the maximum transmit voltage of RF pulse and B1max (18 µT, empirically determined) is the maximum B1 amplitude. σ is the tissue conductivity, ρ is the volumetric mass density, T is the pulse duration and A(t) is the amplitude modulation function of the HS pulse eq.(1). i,j are indices on the p × q dimensional B1ratio - ∆B0 optimization grid.
Simulation: Refocusing performance of the HS pulse could be best represented with the simulated values of | Mx+ iMy | on the inhomogeneity grid of B1+ and ∆B0 after optimization.
2. Image acquisition:
We employed a free‐breathing iNAV motion corrected 3D dual-echo CMRA pulse-sequence (IDEA version E12U-SP01) and combined it with the new optimized T2-prep on a 7T scanner (MAGNETOM Terra, Siemens Healthcare, Erlangen, Germany) (Figure 1). To circumvent the magnetohydrodynamic effect, which is highly prominent at 7T, we employed a pulse oximeter (Siemens Healthcare, Erlangen, Germany) for cardiac synchronization instead of ECG. All the acquisitions were carried out with a body 8Tx/16Rx surface-coil in Trueform (1Tx) mode. The motion-corrected image reconstruction framework used in this work has been described earlier.12–15
RESULTS:
Figure 3 represents the amplitude, frequency and phase modulation waveforms for optimized HS pulse as well as the real and imaginary parts of the HS pulse. The simulated performance of the HS pulse on the B1+ and ∆B0 grids is demonstrated in Figure 4 for cardiac imaging at ultra-high field (7T) with the 8Tx/16Rx surface coil in Trueform (1Tx) mode.Figure 5 represents the phantom images obtained with T2-prep containing conventional HS pulse and our optimized HS pulse. The artefacts at phantom-air interface with the standard T2-prep are greatly reduced in the image obtained with the optimized HS pulse. In the volunteer image, artifacts from magnetic field inhomogeneities (marked with blue arrows) are visible with the standard T2-prep (Figure 5c) but not with the optimized T2-prep (Figure 5d).
CONCLUSION:
We present an optimization algorithm for adiabatic refocusing pulses, that resulted in improved T2-preparation performance at 7T with reduced sensitivity to magnetic field inhomogeneities. Further we demonstrate the successful initial use of a motion-corrected free-breathing 3D dual-echo CMRA pulse-sequence incorporating this T2-prep in low flip-angle phantom and in vivo measurements.Acknowledgements
This work was supported by EPSRC (EP/L015226/1, EP/P032311/1, EP/P007619/1 and EP/P001009/1), the Wellcome/EPSRC Centre for Medical Engineering (NS/A000049/1) and 7T grant (Wellcome Trust Collaboration in Science grant [WT201526/Z/16/Z]).References
1. Terekhov, M. et al. New commercial 8Tx / 16RX array for Clinical 7T Cardiac MRI : initial experience. Proc. Intl. Soc. Mag. Reson. Med. 29 (2021), 2–4.2. Van Elderen, S. G. C. et al. Initial results on in vivo human coronary MR angiography at 7 T. Magn. Reson. Med. 62, 1379–1384 (2009).
3. Snyder, C. J. et al. Initial results of cardiac imaging at 7 Tesla. Magn. Reson. Med. 61, 517–524 (2009).
4. Van Elderen, S. G. C. et al. Right coronary MR angiography at 7 T: A direct quantitative and qualitative comparison with 3 T in young healthy volunteers. Radiology 257, 254–259 (2010).
5. Schmitter, S. et al. Cardiac imaging at 7 tesla: Single- and two-spoke radiofrequency pulse design with 16-channel parallel excitation. Magn. Reson. Med. 70, 1210–1219 (2013).
6. Aigner, C. S., Dietrich, S. & Schmitter, S. Three-dimensional static and dynamic parallel transmission of the human heart at 7 T. NMR Biomed. 34, 1–15 (2021).
7. Schmitter, S., Schnell, S., Uğurbil, K., Markl, M. & Van de Moortele, P. F. Towards high-resolution 4D flow MRI in the human aorta using kt-GRAPPA and B1+ shimming at 7T. J. Magn. Reson. Imaging 44, 486–499 (2016).
8. Moore, J., Jankiewicz, M., Anderson, A. W. & Gore, J. C. Evaluation of non-selective refocusing pulses for 7 T MRI. J. Magn. Reson. 214, 212–220 (2012).
9. Moore, J., Jankiewicz, M., Zeng, H., Anderson, A. W. & Gore, J. C. Composite RF pulses for B1+-insensitive volume excitation at 7 Tesla. J. Magn. Reson. 205, 50–62 (2010).
10. Silver, M. S., Joseph, R. I. & Hoult, D. I. Selective spin inversion in nuclear magnetic resonance and coherent optics through an exact solution of the Bloch-Riccati equation. Phys. Rev. A 31, 2753–2755 (1985).
11. Silver, M. S., Joseph, R. I. & Hoult, D. I. Highly selective π 2 and π pulse generation. J. Magn. Reson. 59, 347–351 (1984).
12. Henningsson, M., Smink, J., Razavi, R. & Botnar, R. M. Prospective respiratory motion correction for coronary MR angiography using a 2D image navigator. Magn. Reson. Med. 69, 486–494 (2013).
13. Bustin, A. et al. 3D whole-heart isotropic sub-millimeter resolution coronary magnetic resonance angiography with non-rigid motion-compensated PROST. J. Cardiovasc. Magn. Reson. 22, 1–16 (2020).
14. Prieto, C. et al. Highly efficient respiratory motion compensated free-breathing coronary MRA using golden-step Cartesian acquisition. J. Magn. Reson. Imaging 41, 738–746 (2015).
15. Cruz, G., Atkinson, D., Henningsson, M., Botnar, R. M. & Prieto, C. Highly efficient nonrigid motion-corrected 3D whole-heart coronary vessel wall imaging. Magn. Reson. Med. 77, 1894–1908 (2017).
Figures
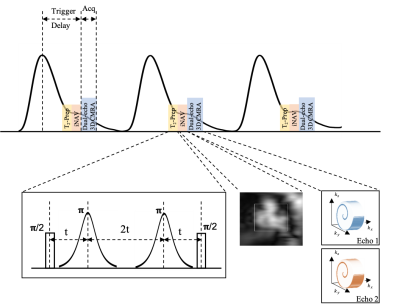
Figure 1: Schematic representation of motion corrected free-breathing dual-echo 3D CMRA pulse-sequence with an accelerated 3D variable density spiral-like Cartesian trajectory with golden angle between spiral-like interleaves (VD-CASPR), preceded by low‐resolution coronal 2D image navigators (iNAVs). To suppress the myocardium signal and enhance the contrast between the coronary arteries and myocardium, a T2-prep is used prior to the iNAVs. The CMRA pulse sequence is shown with respect to the pulse oximeter signal.

Figure 2: The pulse optimization toolbox consisting of the following four modules: 3D Bloch simulation tool, numerical optimization tool for RF pulse, simulation of the optimized RF pulse performance and RF pulse-shape generator for Siemens MR scanners.
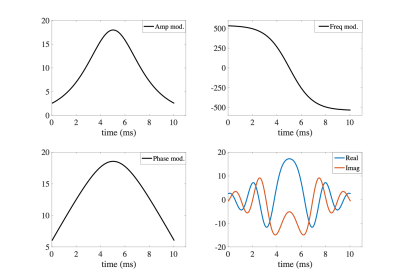
Figure 3: (a-c) Amplitude, frequency and phase modulation waveforms for optimized HS pulse. (d) The real and imaginary parts of the Hyperbolic secant (HS) pulse.
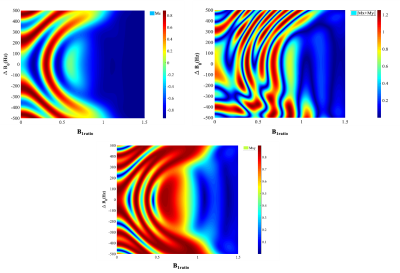
Figure 4: Bloch simulation of HS pulse as a non-selective refocusing pulse. HS pulse performance with respect to B1+ and ∆B0 is demonstrated for cardiac imaging at ultra-high field (7T) with the 8Tx/16Rx surface coil from Rapid in single transmit (1Tx) mode. The color scales represent (a) Mx, (b) My, (c) Mz and (d) |Mx+ My |.
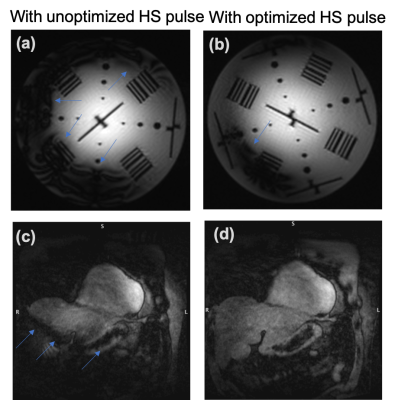
Figure 5: The use of optimized HS pulses in the T2-prep helped minimizing artifacts due to magnetic field inhomogeneity in phantom images compared to the conventional HS pulse (a, b). Sensitivity to field inhomogeneity is also significantly reduced for in vivo data (healthy volunteer, 30 yr, male) obtained with optimized (d) in comparison with the conventional HS pulse (c) (blue arrows). Acquisition parameters: 1.2mm isotropic resolution, TR/TE1/TE2=4.8/1.53/3.06 ms, acceleration factor=4, bandwidth=875 Hz/px.
DOI: https://doi.org/10.58530/2022/1563