1506
Temporally improved volume registration by data driven subvolume interpolation of simultaneous multislice EPI time series1Computer science, University of Geneva, Geneva, Switzerland, 2CIBM, Geneva, Switzerland, 3University of Geneva, Geneva, Switzerland
Synopsis
In the context of EPI time series acquisition, fast motion occurring below the Nyquist limit (< 1 TR), present a problem for accurate registration by 3D rigid-body algorithms. A method for temporally upsampling SMS EPI acquisitions is proposed. EPI volumes are splitted into subvolumes according to the temporal acquisition order of SMS and interpolated using a data driven approach based on pairwise affine transforms and linear interpolation. A proof of concept based EPI acquisitions of controlled head choreographies shows that fast motion below the Nyquist rate can be more accurately estimated by our method.
Introduction
Motion occurring faster than the Nyquist frequency during EPI series acquisition hinders motion estimation by 3D rigid body registration. Thus, we propose a method to alleviate this issue by temporal upsampling of interleaved EPI acquisition by multislice volume splitting and spatial interpolation. The proposed proof of concept is based on head movements, although the upsampling method is general and only assumes interleaved EPI data as input. Typical TR values for full EPI volume acquisitions are of the order of the second although TR = 350 ms has been achieved1. Studies2 have demonstrated that abrupt head motion takes between 200 to 800 ms. Therefore, rapid motion may occur during a TR period, and slice-to-volume registration is necessary to cope with intra-volume motion. Simultaneous multi-slice3 (SMS) acquisition opens the possibility to interpolate subvolumes, hence approximating a complete set of volumes with a higher temporal resolution. Therefore, we propose a data driven method to find pairwise affine transforms between slices in conjunction with linear interpolation.Methods
Technical parameters: our algorithm was tested on series of multislice SMS3 EPI volumes with the following parameters: 36 slices/volume with 4 simultaneous slices/volume and TE = 30 ms, TR = 600 ms. A series of fast abrupt periodic (rotational) movements was performed during the acquisition to demonstrate the upsampling capabilities of our approach, in terms of peak motion amplitude estimation. Indeed, back and forth motion (1 period) that is faster than the acquisition volume (1 TR) will result in decreased motion amplitude estimation. A series of slower motion blocks was also performed for comparison purposes.Interpolation algorithm: The method is based on splitting a single EPI acquisition ( ~ 640 volumes) into multiple time series (TS) based on the temporal acquisition order of the SMS scheme. The number of slices per volume should be a multiple of the SMS factor (i.e. 4) and a divisor of the total number of slices (i.e. 36) while keeping enough spatial information to allow robust interpolation. Among the possible options (4, 12 or 36 slices), 12 was chosen as a good compromise between temporal and spatial resolution. Hence, the time series is separated in 3 interleaved time series (TS1 – TS3).
Missing slices in the resulting subvolumes are non-uniformly arranged due to the given temporal order from SMS (Fig. 1). Each subvolume needs to be spatially interpolated to cope with incomplete spatial coverage. The interpolation algorithm starts by computing optimal forward and backward pairwise affine transforms between adjacent slices. This procedure takes as input the first full volume (36 slices) and searches for the optimal affine transform from slice n to slice n+1 (forward) as well as from slice n to n-1 (backward) using a MSE metric and gradient descent. Subvolumes were interpolated by weighted averages of backward and forward transforms of existing slices.
Registration method: Each of the interpolated time series is then realigned with respect to its first (fully interpolated) volume (Fig. 1 (a)). The fully (3x) upsampled signal is reconstructed by temporally interleaving the motion parameters vectors (Fig. 1 (b)) . The realignment algorithm used here was “intensity based”, i.e., based on a MSE metric between volumes, which provides better results compared to “feature based” methods such as an extension of the SIFT4 algorithm adapted for 3D image registration.
Results
Full reference volume (first data point, no interpolation) and interpolated subvolume corresponding to the second data point are displayed in Fig. 2. Qualitative comparison shows an good overall morphological consistency.Fig. 3 shows the original time series (no interpolation, in blue) of the estimated motion parameters based on full volume realignment obtained with SPM5. The upsampled signals of the same acquisition (in red and green) are superimposed to show the increase in signal amplitude for abrupt fast motion and similar amplitude for slower motion blocks.
Discussion
Motion parameters, such as rotation angle reported in Fig.3, are underestimated when fast motion (< TR) occurs. Temporal upsampling together with spatial interpolation is able to capture motion occurring below the Nyquist limit imposed by TR. Therefore a significant improvement in abrupt motion estimation can be obtained. However, slower motion blocks’ s amplitudes do not change, which is expected given that the motion speed in that case is much slower than the sequence sampling period. This concurs with our hypothesis that motion that is faster than the sampling rate of a single volume would result in decreased signal amplitude.Conclusion
This work proposes a new general post-processing spatio-temporal upsampling method to resolve faster than repetition time (or volume acquisition time) motion in interleaved EPI acquisitions. Subsequent 3D rigid-body motion estimation may be significantly improved for abrupt motion. We expect that this method can benefit to the MRI community, e.g., for sub-volume motion correction.Acknowledgements
No acknowledgement found.References
1. Jahanian, H., Holdsworth, S., Christen, T., Wu, H., Zhu, K., Kerr, A.B., Middione, M.J., Dougherty, R.F., Moseley, M. and Zaharchuk, G., 2019. Advantages of short repetition time resting-state functional MRI enabled by simultaneous multi-slice imaging. Journal of neuroscience methods, 311, pp.122-132.
2. Fang, Y., Nakashima, R., Matsumiya, K., Kuriki, I. and Shioiri, S., 2015. Eye-head coordination for visual cognitive processing. PloS one, 10(3), p.e0121035.
3. Feinberg, D.A. and Setsompop, K., 2013. Ultra-fast MRI of the human brain with simultaneous multi-slice imaging. Journal of magnetic resonance, 229, pp.90-100.
4. B. Rister, M. A. Horowitz and D. L. Rubin, "Volumetric Image Registration From Invariant Keypoints," in IEEE Transactions on Image Processing, vol. 26, no. 10, pp. 4900-4910, Oct. 2017. doi: 10.1109/TIP.2017.2722689
5. Penny, W.D., Friston, K.J., Ashburner, J.T., Kiebel, S.J. and Nichols, T.E. eds., 2011. Statistical parametric mapping: the analysis of functional brain images. Elsevier.
Figures
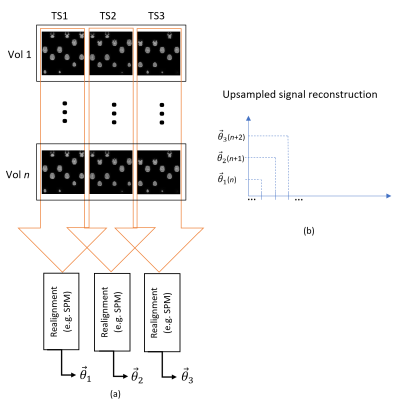
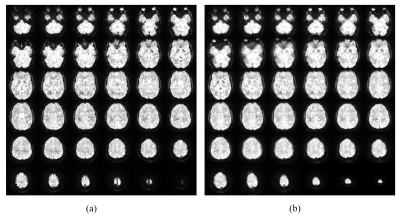
Figure 2 Reference full volume (a) and interpolated subvolume (b). Both volumes are temporally acquired at the beginning (volumes #1 and #2, respectively) of the EPI acquisition (~640 volumes) before motion occurrence. Volumes are normalized with the 95th percentile.
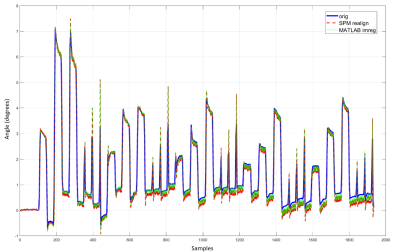
Figure 3 Upsampled signals superimposed on original signal. Original (blue) refers to realigned signal without using our upsampling method (i.e., using full raw volumes) whereas the red and green signals are reconstructed from the 3 time series motion parameters obtained by realigning the interpolated partial volumes.