1503
Estimation of numerical substrate properties with compartmentalized models from Monte-Carlo simulated DW-MRI signals1Signal Processing Laboratory (LTS5), Ecole Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2CIBM Center for Biomedical Imaging, Lausanne, Switzerland, 3Radiology Department, Centre Hospitalier Universitaire Vaudois and University of Lausanne, Lausanne, Switzerland
Synopsis
For over a decade, microstructure imaging has been a hot research topic in DW-MRI. Tissue complexity compelled researchers to make assumptions about certain properties. The inverse problem of microstructure imaging, in particular, is ill-posed, and current methods fix some parameters to reduce the solution space. In this abstract, we look at how intracellular and extracellular diffusion coefficients affect the estimation of compartmentalized model parameters. We show that robust estimation of some parameters does not extend to all parameters using Monte-Carlo simulations in impermeable substrates with multiple diffusivities, and we identified the extracellular compartment as the most influential on estimation quality.
Introduction
Monte-Carlo diffusion simulations (MCDS) showed promising results for realistic diffusion-weighted magnetic resonance imaging (DW-MRI) signal generation1,2,3. In-silico experiments offer the opportunity to test and validate new models of tissue microstructure. In this work, we use MCDS to investigate the bias of parameters estimation of compartmentalized models when fixing the diffusion coefficient in substrates composed of a collection of spheres of gamma-distributed radii.Methods
In this work, we used the three-compartment model VERDICT4 designed for microstructure estimation of spherical cells. Among the parameters of the model, we estimated the intra-cellular (fin), extra-cellular (fex) and the vascular (fv) volume fractions, the average cell radius (R), and the intra-/extra-cellular diffusion coefficients (Di, De) with the Levenberg-Marquardt (LM) optimization algorithm5 . Because diffusion signals in our substrates were isotropic, the main direction of the vascular compartment was not relevant. We fixed the pseudo diffusion coefficient to 8 10⁻⁹ m2/s 6 and constrained the sum of the volume fractions to one. We fitted the model with four different constraints on Di and De for investigating their influence on the parameters’ estimation. We fixed them in two cases, either to the ground-truth or to widely-used fixed values (0.5 and 2 10⁻⁹ m2/s)5,6. In the third and fourth cases, we estimated them with coupled equality or left them unconstrained. R, fin, and fex were estimated during the optimization procedure.We simulated the DW-MRI signals with an extended version of the publicly available MCDC simulator1, adapted to simulate diffusion in substrates with distinct Di and De. Substrates were single-voxel cubes of side length 70 μm filled with spheres of radii sampled from a gamma distribution of mean 1.5 μm and variance 0.75 μm2. We used four substrates having fin from 0.3 to 0.6 (Fig.1). Di and De were 1,2 or 3 10⁻⁹ m2/s, and 0.1, 0.5 or 1 10⁻⁹ m2/s, respectively. For all simulations, 3.5×105 particles were randomly initialized within the substrates and diffused during 50 ms. The time step was set to 5 μs, and the step length is calculated with $$$\delta s=\sqrt{6D \delta t}$$$ for each compartment. DW-MRI signals were generated with a PGSE sequence with TE= 50 ms and $$$\delta= 4.5 ms$$$ in 24 directions for three b-shells(1, 2 and 4 109 s/m2). Each signal was corrupted 30 times with Rician noise7 for three signal-to-noise ratios (SNR) (20, 50, and 100).
Results and discussion
The quality of the estimation of fin and fex depends on De of the substrate mostly. For De = 0.1 10-9 m2/s, fex is underestimated while fin is overestimated for all pairs (Di, De) and all methods (see Fig. 2, left column). Fig.3 shows the MAE on fin that ranges from 0.05 for ground-truth to 0.5 for fixed method. As De increases, Fig. 2 shows an improvement in fin and fex estimates for all models. The coupled (green) and unconstrained (red) models best estimate fin with an error from 0.01 to 0.05 and variance under 0.08. The error of the model with ground-truth parameters remains stable, and the fixed model provides the worst estimations for most cases.The true value of De also drives the estimates of Di and De with the coupled and unconstrained models. Fig. 4 shows that the diffusion coefficient estimated by the coupled model (right) is close to De. When the optimization is unconstrained (left), Di and De estimates are different but De is close to the coupled models. Even with the unconstrained model, Di estimations follow the trends of the true De (black triangle). Finally, the variance of De and Di estimations increases and decreases with De for both models respectively.
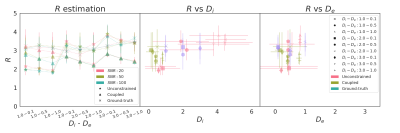
R estimates range from 2 to 4 μm, as shown in Fig. 5. The ground-truth (cross) model provides a more stable estimation across (Di, De) pairs and SNR (left). The center plot shows that the unconstrained model compensates the bad estimation of Di by an overestimation of the cell radius (Center). Conversely, De has little influence on R.
Conclusion
Even if the substrates are designed to match the assumptions of the compartmentalized model, estimating the diffusion coefficients remains a challenging problem. Because R and Di have opposing effects on the signal, estimating both parameters is difficult. MCDS is a promising tool for studying the effect of tissue properties on DW-MRI signals. Future work will focus on testing new methods with MCDS to better disentangle model parameters estimation.Acknowledgements
This work is partly supported by the Swiss National Science Foundation under grant Nbr 205320_175974 and Erick J. Canales-Rodríguez was supported by the Swiss National Science Foundation (SNSF, Ambizione grant PZ00P2_185814). We acknowledge access to the facilities and expertise of the CIBM Center for Biomedical Imaging, a Swiss research center of excellence founded and supported by Lausanne University Hospital (CHUV), University of Lausanne (UNIL), Ecole polytechnique fédérale de Lausanne (EPFL), University of Geneva (UNIGE) and Geneva University Hospitals (HUG).
References
1. Rafael-Patino, J., Romascano, D., Ramirez-Manzanares, A., Canales-Rodríguez, E. J., Girard, G., & Thiran, J. P. (2020). Robust Monte-Carlo simulations in diffusion-MRI: Effect of the substrate complexity and parameter choice on the reproducibility of results. Frontiers in neuroinformatics, 14, 8.
2. Lee, H. H., Fieremans, E., & Novikov, D. S. (2021). Realistic Microstructure Simulator (RMS): Monte Carlo simulations of diffusion in three-dimensional cell segmentations of microscopy images. Journal of Neuroscience Methods, 350, 109018.
3. Fieremans, E., Novikov, D. S., Jensen, J. H., & Helpern, J. A. (2010). Monte Carlo study of a two‐compartment exchange model of diffusion. NMR in Biomedicine, 23(7), 711-724.
4. Panagiotaki, E., Walker-Samuel, S., Siow, B., Johnson, S. P., Rajkumar, V., Pedley, R. B., ... & Alexander, D. C. (2014). Noninvasive quantification of solid tumor microstructure using VERDICT MRI. Cancer research, 74(7), 1902-1912.
5. Panagiotaki, E., Schneider, T., Siow, B., Hall, M. G., Lythgoe, M. F., & Alexander, D. C. (2012). Compartment models of the diffusion MR signal in brain white matter: a taxonomy and comparison. Neuroimage, 59(3), 2241-2254.
6. Bonet‐Carne, E., Johnston, E., Daducci, A., Jacobs, J. G., Freeman, A., Atkinson, D., ... & Panagiotaki, E. (2019). VERDICT‐AMICO: Ultrafast fitting algorithm for non‐invasive prostate microstructure characterization. NMR in Biomedicine, 32(1), e4019.
7. Garyfallidis, E., Brett, M., Amirbekian, B., Rokem, A., Van Der Walt, S., Descoteaux, M., & Nimmo-Smith, I. (2014). Dipy, a library for the analysis of diffusion MRI data. Frontiers in neuroinformatics, 8, 8.
Figures
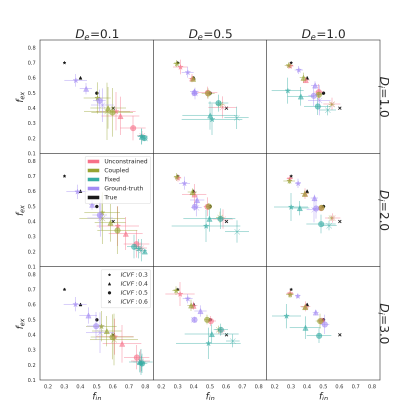
Figure 2: Scatter plots of fin and fex estimations for all (Di, De) μm2/ms pairs (subplot), all fin (symbol) and all methods (colors) (SNR=20). Colored and black symbols are the results and the ground truth respectively. An overestimation of fin or an overestimation of fex results in a colored symbol at the right or above the corresponding black symbols, respectively. Each symbol is located at the mean (fin , fex) estimated from the 30 noisy signals, and the bars are the variance of the estimations.
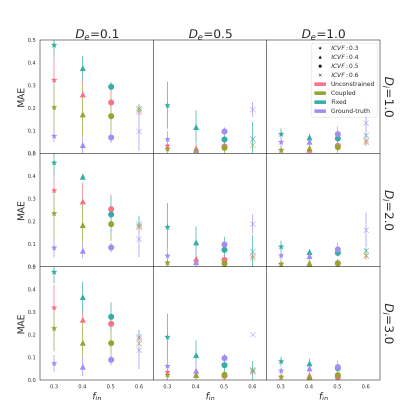
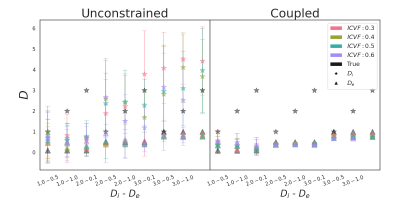
Figure 4: Estimation of Di (star) μm2/ms and De (triangle) μm2/ms for the Unconstrained (left) and Coupled (right) model parameters for all fin (SNR=20). Colored and black symbols are for the estimated and the true fin respectively. Each symbol is located at the mean estimation from the 30 noisy signals, and the bar is the corresponding variance.