Introduction

Several qMRI techniques have been described in the literature for mapping separately the myelin¹ and iron² distributions in the brain. Nevertheless, this remains an active field of research due to the important medical implications of quantifying myelin and iron content. An unmet need to map the spatial distribution of free water exists and could be important from both clinical and theoretical standpoints, based on the notion that free water relaxation in the brain could serve as a testing ground for the dipolar MR relaxation theory of Bloembergen-Purcell-Pound (BPP). The purpose of this work was to develop an integrated theoretical model and computer algorithms for mapping the spatial distributions of free water together with myelin and iron, as an application of multiparameter (MP-) qMRI of R1, R2, and the water-normalized proton density (nPD). We study the relationships between R1, R2, and nPD as functions of the free water density in a sub-sample of a cohort of 15-year-old adolescents born extremely preterm.

Theory

We formulate a fast exchange relaxation (FER) model in which R1 is driven by the dipole-dipole interactions in free water (Figure 1) and magnetization exchange phenomena resulting from water interacting with myelin. In turn, R2 relaxation includes these two relaxation mechanisms plus spin dephasing processes caused by the magnetic field inhomogeneities associated to iron deposits. Accordingly, the relaxation rates of the longitudinal and transverse magnetizations are respectively given by:

Eq. 1: $$$R1\left(\overrightarrow{x}\right)=\alpha_f\left(\overrightarrow{x}\right)R1_f+\alpha_{Myelin}\left(\overrightarrow{x}\right)R1_{Myelin}$$$

and,

Eq. 2: $$$R2\left(\overrightarrow{x}\right)=\alpha_f\left(\overrightarrow{x}\right)R2_f+\alpha_{Myelin}\left(\overrightarrow{x}\right)R2_{Myelin}+\alpha_{Fe}\left(\overrightarrow{x}\right)R2_{Fe}$$$

In these, $$$\overrightarrow{x}$$$ designates a voxel position, α_f, α_Myelin, and α_Fe are the densities of free water in the intra- and extra-cellular compartments, trapped within the myelin sheaths compartment, and exposed to the magnetic field inhomogeneities caused by iron, respectively.

We solve the FER system of equations above by iterating on $$$\alpha_{f}\left(\overrightarrow{x}\right)$$$ finding:

Eq. 3: $$$\alpha_{Myelin}\left(\overrightarrow{x}\right)\approx\lim_{Large R1_w}\left(SyTx_{R1}\left(\overrightarrow{x},R1_w\right)-\alpha_f(\overrightarrow{x})\frac{R1_f}{R1_w}\right)\times\frac{R1_w}{R1_{Myelin}}$$$

and,

Eq. 4: $$$\alpha_{Fe}\left(\overrightarrow{x}\right)\approx\lim_{Large R2_w}\left(SyTx_{R2}\left(\overrightarrow{x},R2_w\right)-\alpha_f(\overrightarrow{x})\frac{R2_f}{R2_w}-\alpha_{Myelin}(\overrightarrow{x})\frac{R2_{Myelin}}{R2_w}\right)\times\frac{R2_w}{R2_{Fe}}$$$

and finally for free water, by recasting Eq. 1:

Eq. 5: $$$\alpha_f\left(\overrightarrow{x}\right)=\frac{R1\left(\overrightarrow{x}\right)-\alpha_{Myelin}\left(\overrightarrow{x}\right)R1_{Myelin}}{R1_f}$$$

In the equations above, we have used the synthetic texture definitions:

Eq. 6: $$$SyTx_{R1,2}\left(\overrightarrow{x},R1,2_w\right)\equiv\left(1-\exp\left(\frac{-R1,2\left(\overrightarrow{x}\right)}{R1,2_w}\right)\right)$$$

Methods

This study was approved by the Institutional Review Board of the University of North Carolina at Chapel Hill (UNC-CH), a participating institution of the Extremely Low Gestational Age Newborn – Environmental Influences on Child Health Outcomes (ELGAN-ECHO) Study. A sub-sample of 38 participants (19 females and 19 males, mean age: 15.4 ± 0.4 years) from the ELGAN-ECHO population who underwent brain MP-qMRI at a single site were evaluated with a 3T MRI protocol using the triple turbo spin echo (TSE) pulse sequence. This triple weighting acquisition consists of concatenated long repetition time dual echo turbo spin echo (DE-TSE) and short repetition time single echo turbo spin echo (SE-TSE) sequences implemented with identical scan geometry and receiver settings. Typical imaging parameters: voxel = 0.5x0.5x2 mm³, TE_1,2eff = 12 ms, 102 ms, TR_long = 10 s, TR_short = 0.5 s, with a 7:34 minutes scan time. Participant images were free of braces-induced magnetic susceptibility and severe motion artifacts. The image processing pipeline (IPP) consists of segmentation functions and mapping algorithms programmed in Python (version 3.8.11) with the Anaconda Navigator (version 2.0.4). nPD-R1-R2 qMRI maps were calculated according to the Bloch equation solution as applicable for the triple TSE pulse sequence. The MP-qMRI maps were processed to create synthetic R1 and R2 texture maps (Eq. 6). The IPP then calculates iteratively maps of myelin, iron, and free water content according to Eq. 3-5, respectively. Linear regression analysis was performed to assess whether a significant association existed between the mean MP-qMRI outcomes and free water density (P < 0.05).

Results

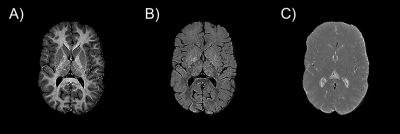
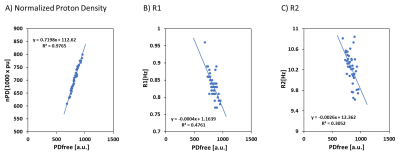
Representative myelin, iron, and free water maps are shown in Figure 1. Notably the free water map shows minor white-to-gray matter contrast, confirming the free water homeostasis premise as implied by diffusion MRI, i.e., by the very low white-to-gray matter contrast observed in mean diffusivity maps. The relaxation rates of the longitudinal and transverse magnetizations are negatively correlated with the free water proton density, as shown in Figure 2.

Discussion and Conclusion

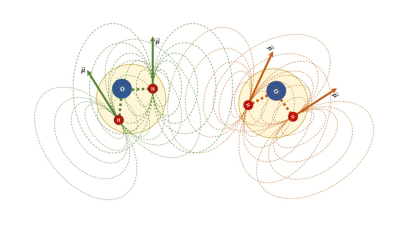
A theoretical framework and IPP for mapping the distribution of free water has been developed and tested with a cohort of adolescents born extremely preterm. This work could have clinical applications for assessing pathologies accompanied by alterations in free water as well as theoretical projections for modeling the intra- and inter-molecular aspects of dipole-dipole interactions (Figure 3) in brain tissue.

Acknowledgements

This work was supported in part by the National Institute of Neurological Disorders and Stroke (5U01NS040069-05 and 2R01NS040069-09), National Institutes of Health Office of the Director (5UH3OD023348-06), and the National Institute of Child Health and Human Development (5P30HD018655-28).