Introduction

Morphological and functional imaging of the lung is of great importance for diagnosis and monitoring of prevalent pulmonary diseases¹. To this end, many non-contrast-enhanced techniques have been developed to assess lung morphology and local pulmonary function. To achieve this, these methods rapidly acquire time-resolved images to capture ventilation and perfusion information during free breathing. Therefore, parallel imaging with readout asymmetry is commonly utilized with these protocols.

Although many preceding works have focused on pulse sequence design² or post-processing techniques³ for the identification of pulmonary information, one overlooked aspect has been the image reconstruction, where GRAPPA is commonly used for reconstruction. In this work, we incorporate a recently developed framework for the reconstruction of undersampled acquisitions, namely low-rank modeling of local k-space neighborhoods (LORAKS)⁴. We present in vivo results to show the feasibility and demonstrate the performance of LORAKS compared to GRAPPA in Fourier Decomposition (FD) MRI.

Methods

In FD MRI, 2D bSSFP sequence is utilized with uniform undersampling of phase encodes, to capture fast signal changes regarding cardiac and respiratory cycles. Afterwards, these accelerated acquisitions are reconstructed to recover the missing k-space lines followed by the Fourier Decomposition (FD) analysis on registered time-series images to generate ventilation- and perfusion-weighted maps.

To reconstruct accelerated acquisitions, many methods have been developed by exploiting linear dependencies in MR acquisitions. Among these, GRAPPA has been widely used to estimate linear dependencies between k-space samples from different receiver coils using fully sampled calibration region and has been used in FD MRI techniques to recover missing k-space information in accelerated acquisitions. Since then, novel recovery methods have been developed to further exploit linear dependencies in the acquisitions based on the theory of low-rank matrix recovery. A recent framework that exploits this low-rank structure is LORAKS framework, which observes that the system matrix with smoothness of image phase, finite extent of spatial support and availability of multiple receiver channels can be casted as a structured low-rank matrix. Here, we have utilized LORAKS with the accelerated time-resolved lung acquisitions. As such, reconstructions were obtained by solving the following optimization problem:
$$arg\min_{x} J_r(P_S(x))$$
$$subj. to: \mathbb Ax=x_{acq}$$
where $$$J_r(\cdot)$$$ is a nonconvex function that encourages its argument to have rank less than or equal to $$$r$$$, $$$P_S(\cdot)$$$ is the operator that constructs the structured low-rank matrix, $$$\mathbb A $$$ denotes sampling operator, $$$x_{acq}$$$ denotes acquired data, and $$$x$$$ denotes data to be estimated. In this work, we have used a novel heuristic approach inspired by Iyer et al.⁵ to automatically select the rank threshold term $$$r$$$ based soft-thresholding of singular values of the system matrix by interpreting LORAKS as a denoiser with Hermitian-symmetry and low-rank properties. As such, the pseudo-optimal matrix rank ($$$r^*$$$) can be obtained via Stein’s unbiased risk estimate:
$$arg\min_{r} ||P_S(x_{acq}-y) ||_2^2 \approx arg\min_{r}SURE_{P_S}(x_{acq})=r^*$$
After obtaining reconstructions, individual coil images were Hamming filtered and combined using adaptive coil combination method⁶. Afterwards, combined magnitude images were registered, and FD analyses of the registered time-series were performed to obtain ventilation and perfusion maps as previously suggested⁷.
For evaluation, in vivo bSSFP acquisitions were obtained from three volunteers using a 1.5T scanner (Magnetom Aera, Siemens Healthineers, Germany) with TR/TE = 1.88/0.80 ms, GRAPPA factor = 3, slice thickness = 15 mm, asymmetrical echo readout, and a 0.2 s pause between measurements. For each volunteer, FD was performed using 200 images from the steady state.
To assess the image quality, parenchymal contrast-to-noise ratio (CNR) and mean signal intensities were calculated on generated functional maps. CNR was defined as the ratio of mean functional map amplitude within the lung parenchyma and air region and was calculated on maps generated by the FD method, whereas the mean signal intensities were calculated as the averaged signal intensity in the lung parenchyma from quantitative functional maps.

Results

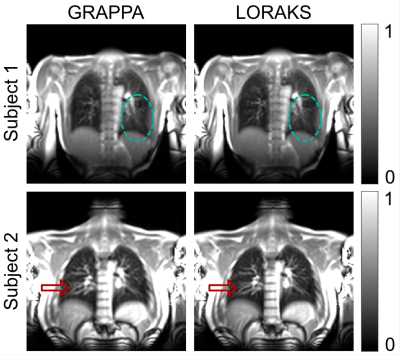
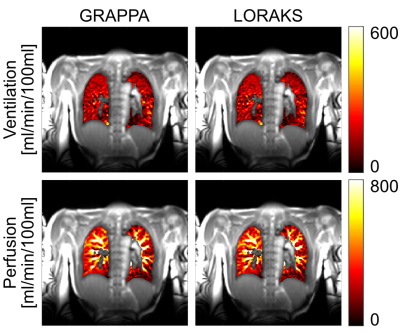
Figure 1 shows representative magnitude images obtained with GRAPPA and LORAKS from two subjects. While both methods can reconstruct images successfully, LORAKS is able to recover higher spatial-frequency features and dampens aliasing artifacts more successfully.
Figure 2 displays representative quantitative ventilation and perfusion maps obtained with both methods, overlaid on magnitude images. Both methods can generate functional maps successfully with similar signal intensities. Nonetheless, by recovering higher spatial-frequency features, LORAKS provides improved vessel depiction in the perfusion maps.
Tables 1 and 2 show the CNR and mean signal intensities averaged across the subjects. We observe that the functional maps obtained with LORAKS reconstruction tends to improve the CNR compared to GRAPPA in both ventilation and perfusion maps by improving aliasing artifact suppression. Meanwhile, both methods provide similar mean signal intensities in the quantitative maps.

Discussion & Conclusion

We have developed and demonstrated a novel framework for improved reconstruction quality in functional lung imaging using LORAKS reconstructions. Magnitude, ventilation- and perfusion-weighted images were successfully obtained with LORAKS via a novel automated rank selection strategy. While further studies with more subjects are warranted, our preliminary results indicate that LORAKS can be a viable alternative to GRAPPA reconstructions used in FD MRI, to improve image and functional map quality.

Acknowledgements

This work was supported by Deutsche Forschungsgemeinschaft (grant number: DFG 397806429).