Introduction

MRI at UHF offers great promises in SNR and CNR. In the quest of reaching ever higher magnetic fields, one crucial aspect beforehand remains the design of the magnet, the gradient coil and their interaction. The time-varying fields generated by the gradient cause eddy-currents in the structure which, under the influence of a strong B₀ field, generate vibrations, which engender themselves electric fields and power deposition in the He bath. In addition to these power losses which can be critical for the integrity of the magnet, mechanical resonances also can be detrimental for imaging performance (e.g. ghosting). In this context, we report in this work vibration measurements on the SC72 Siemens Healthineers whole-body gradient in the bore of the Iseult magnet at 3T, 7T, 10.2T and 11.7T.

Methods

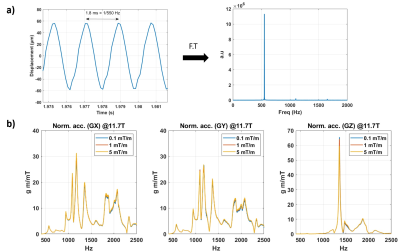
The Iseult magnet¹ is 5 m long/wide and weighs 132 tons. The main superconducting coil is immerged into a He bath of 7000 liters cooled down to 1.8 K, where He is superfluid. The gradient coil is surrounded by a lead tube to screen gradient-magnet interactions at some frequencies². Six mono-axial accelerometers (Hottinger Bruel & Kjaer, Naerum, Denmark) were glued on the gradient, the lead tube and the cryostat to measure accelerations along the X and Y directions (Fig. 1). Vibrations were measured by applying a 1-min chirp excitation on the 3 gradient axis separately with G=1 mT/m over the 0-3200 Hz range. Close to a well-defined natural frequency ω₀, the response of the accelerometers on the gradient was temptingly modeled with a damped harmonic oscillator: $$$\ddot{u}+\eta \dot{u} + \omega_0^2u=F(t)/m$$$, where m is an effective mass and where the damping coefficient η shall vary with B₀. Because of the Lorentz force, the force should be proportional to the current (thus gradient strength) and the static field, i.e. $$$F \propto I B_0$$$. For an oscillating force at angular frequency ω, assuming a large quality factor, solving the differential equation in the steady state yields approximately for the peak displacement $$$u_{max} \propto IB_0/\eta$$$. To verify this simple model, measurements were performed at 0.1, 1 and 5 mT/m to confirm the linearity of the response versus I, for B₀ constant. They were finally repeated on the same identical system at 3T, 7T, 10.2T and 11.7T to study the response and the dependence of η on B₀ over a broad frequency range.

Results

Fig.2.a. shows the measured temporal displacement along the Y axis for a sine excitation of GY=20 mT/m at 550 Hz and at 7T, with its Fourier transform. Fig.2.b shows acceleration spectra acquired at 11.7T for the three gradient axis and normalized by the different gradient strengths. The plots being nearly identical and the system responding at the frequency of the excitation indicate a behavior consistent with a harmonic oscillator. Fig. 3 shows the acceleration spectra under a G=1 mT/m excitation at different B₀ field strengths and for the three gradient axis, showing qualitatively the same behavior aside from expected increased amplitudes versus field strength. The amplitudes of the peaks, normalized to the ones at 3T, are shown in Fig. 4 and reveal a response that grows slower than the B₀ field.

Discussion and conclusion

To a good approximation, the experimental results show that the vibration response at one location of the gradient coil is consistent with a damped harmonic oscillator. The data reveal a less severe dependence for the response than with B₀, which could explain moderate increases of acoustic noise versus field strength³ for a same set up. Having $$$\eta \propto B_0$$$ would yield a nearly constant amplitude response versus B₀, which is not the case. Interestingly, some resonances also exhibit a plateau which could be consistent with a dependence of the damping coefficient as $$$\eta(\omega) \propto \eta_0(\omega) + \alpha B_0$$$ (with α being a scalar). The data, at least up to 11.7T, on the other hand cannot verify a dependence as $$$\eta(\omega) \propto \eta_0(\omega) + \alpha B_0^2$$$ as suggested in the literature⁴ which would imply an increase of the response until a maximum is reached, followed by a drop versus field strength.

Acknowledgements

NB is funded by the European Union’s Horizon 2020 research and innovation program under grant agreement No 885876 (AROMA project). We thank Hermann Landes for valuable discussions. François Nunio and Loris Scola are also thanked for the fruitful discussions about the mechanics during the tests.