1364
A dictionary-based approach for the determination of pH values using 31P MRS
Vanessa L. Franke1,2, Johannes Breitling1, Renate Bangert1, Mark E. Ladd1,2,3, Peter Bachert1,2, and Andreas Korzowski1
1Division of Medical Physics in Radiology, German Cancer Research Center (DKFZ), Heidelberg, Germany, 2Faculty of Physics and Astronomy, University of Heidelberg, Heidelberg, Germany, 3Faculty of Medicine, University of Heidelberg, Heidelberg, Germany
1Division of Medical Physics in Radiology, German Cancer Research Center (DKFZ), Heidelberg, Germany, 2Faculty of Physics and Astronomy, University of Heidelberg, Heidelberg, Germany, 3Faculty of Medicine, University of Heidelberg, Heidelberg, Germany
Synopsis
The determination of tissue pH under varying cellular conditions by means of 31P MRS is challenging. We propose a concept for a dictionary-based approach for pH estimation under different chemical conditions. As proof-of-concept, we demonstrate its feasibility for a limited subset of conditions using the chemical shifts of ATP and their dependence on pH and magnesium. For the presented subset, the estimated pH values are in good agreement with the prepared values. However, for application to in vivo data, an extension of the dictionary to include other influences, e.g. of other ions, is required and the subject of ongoing work.
Introduction
The pH value of living tissue is a valuable biomarker for numerous pathologies, e.g. cancer. A non-invasive technique for the determination of pH in vivo is phosphorus (31P) magnetic resonance spectroscopy (MRS). As gold standard, the pH-dependent chemical shift of inorganic phosphate (Pi) is used for pH calculation via a modified Henderson-Hasselbalch equation, assuming physiological conditions1. However, challenges of this method are (I) altered ion homeostasis in pathologies and (II) the low signal of Pi in vivo.In general, the measured chemical shifts of 31P compounds are dependent on pH, but to varying extent. Also the concentration of other ions, e.g. magnesium (Mg), sodium (Na), potassium (K), influences the chemical shifts directly or indirectly (i.e. due to change of pK values)2-5. Obtaining the information of multliple 31P resonances under various conditions allows the implementation of a dictionary from which measured chemical shifts can be mapped to the most probable pH values. Such a dictionary would have the benefit of (I) being more robust to changing chemical conditions across different tissues and (II) enabling pH estimation in cases where the Pi signal is too low.
We propose a dictionary-based approach for the estimation of pH values under various chemical conditions using multiple chemical shifts of 31P compounds. Starting from a limited number of samples, the space of dictionary entries is extended using empirically developed approximations of the Hill equation to cover a range of conditions expected in vivo. We demonstrate the feasibility of this approach on a limited subspace using the chemical shifts of adenosine-5’-triphosphate (ATP) and their dependencies on pH and Mg.
Methods
A total of 154 model solutions with a base concentration of 5mM Pi, ATP and phosphocreatine (PCr) were prepared with different pH values and concentrations of Mg, Na and K. 31P spectra of all model solutions were acquired at a 9.4T small-animal scanner (Bruker BioSpec) with an unlocalized FID sequence at a temperature of 37°C. Evaluation of data was performed in MATLAB R2020a (The Mathworks). The chemical shifts of PCr, Pi and ATP were quantified using a home-built implementation of the AMARES algorithm6,7.For demonstrating the concept, we focused on a subset of 24 model solutions with [Na]$$$\,$$$=$$$\,$$$29mM, [K]$$$\,$$$=$$$\,$$$160mM, and the limited pH range [6.8–7.4], for which the dependency of the chemical shifts δi of ATP on the pH value and the ratio R$$$\,$$$=$$$\,$$$[Mg]/[ATP] can be described by empirically developed approximations of the Hill equation:$$\delta_{i}(pH,R)=k-\frac{m\cdot(pH-7.1)+b}{1+\exp(d\cdot{R})}, i=\alpha,\beta,\gamma.\qquad\qquad(1)$$Equation 1 was fitted to the quantified chemical shifts of γ, α and β-ATP, resulting in three defined functions δγ(pH, R), δα(pH, R) and δβ(pH, R). These relations define the dictionary, allowing for an assignment of input values δγ,input, δα,input, δβ,input to possible pairs of pH and R values.
To incorporate uncertainties in the input chemical shifts$$$\,\sigma_{\delta_{i}}\,$$$(assumed to be 0.01$$$\,$$$ppm), pH was calculated as a normal probability density function$$$\,\mathcal{N}(\mu,\,\sigma^{2})\,$$$using Gaussian error propagation:$$P_{i}(pH,R)=\mathcal{N}\left(pH(\delta_{i})|_{R},\left(\frac{\partial{pH}}{\partial{\delta_{i}}}\sigma_{\delta_{i}}\right)^2\right)\qquad\qquad(2)$$ with $$pH(\delta_{i},R)=-\frac{(\delta-k)\cdot(1+\exp(d\cdot{R}))+b}{m}+7.1.\qquad\qquad(3)$$The estimated pH value is then obtained as the weighted mean pH over the joint probability density function (product of all Pi(pH,R)) with the weighted standard deviation as error estimate: $$pH_{est}=\frac{\sum_{pH,R}pH\cdot\prod_{i}P_{i}}{\sum_{pH,R}\prod_{i}P_{i}}.\qquad\qquad(4)$$
Results
The acquired spectra from the model solutions were of good quality, enabling a robust quantification of the chemical shifts of all contained metabolites and showing clear spectral changes with changing pH (Fig.$$$\,$$$1A) and R (Fig.$$$\,$$$1B). For the investigated subspace of pH$$$\,$$$=$$$\,$$$[6.8–7.4] and R$$$\,$$$=$$$\,$$$[0-2], the dependency δi(pH,R) described by Eq.1 is reasonable (Fig.$$$\,$$$2).The obtained relations δi(pH,R) were used to calculate probability density functions Pi(pH,R) (Eq.3) for specific input values δi,input. For the shown example (Fig.$$$\,$$$3), the estimated values pHest$$$\,$$$=$$$\,$$$7.25$$$\,$$$±$$$\,$$$0.05 (with Rest$$$\,$$$=$$$\,$$$0.77$$$\,$$$±$$$\,$$$0.01) are in good agreement with the prepared conditions pHprep$$$\,$$$=$$$\,$$$7.2 and Rprep$$$\,$$$=$$$\,$$$0.75.
When applying this method to all datasets of the shown subspace, the estimated pH values are in good agreement with the prepared values for datasets with small R (Fig.$$$\,$$$4). For the datasets with higher R, the estimated pH values deviate more strongly from the prepared values (Fig.$$$\,$$$4B)
Discussion
We demonstrated the concept of pH estimation by a dictionary-based approach using multiple chemical shifts of 31P metabolites for the example of ATP under different chemical conditions i.e. [Mg]. For the presented subset of model solutions, the estimated pH values are in good agreement with the prepared values. However, the increasing deviations (pHest$$$\,$$$-$$$\,$$$pHprep) for increasing R indicate the need for further refinement of the assumed relation δi(pH,R) for the range of pH$$$\,$$$=$$$\,$$$[6.8-7.4] and R$$$\,$$$=$$$\,$$$[0-2]. Compared to earlier approaches utilizing complete titration curves2,3, the herein proposed approach requires only a reduced number of samples within a specific range of chemical conditions, which simplifies its implementation. For the application to in vivo data, the dictionary needs to be further extended by additional influences, e.g. of other ions. This extension can be done in a similar way as demonstrated, resulting in multidimensional relations δi(pH,R,[K],[Na]), and is currently under investigation utilizing the entire set of 154 model solutions.Conclusion
We proposed a dictionary-based approach for pH estimation using 31P MRS under various chemical conditions and demonstrated its feasibility for a limited subspace using the chemical shifts of ATP and their dependencies on pH and Mg. Further refinement and extension of the dictionary by other influences is, however, required for potential application to in vivo data.Acknowledgements
No acknowledgement found.References
1. de Graaf RA. In Vivo NMR Spectroscopy: Principles and Techniques: 2nd Edition.; 2007. doi: 10.1002/9780470512968.2. Pettegrew JW, Withers G, Panchalingam K, Post JFM. Considerations for brain pH assessment by 31P NMR. Magn. Reson. Imaging 1988;6:135–142 doi: 10.1016/0730-725X(88)90443-2
3. Williams GD, Mosher TJ, Smith MB. Simultaneous Determination of Intracellular Magnesium and pH from the Three 31P NMR Chemical Shifts of ATP. Anal. Biochem. 1993;214:458–467 doi: 10.1006/ABIO.1993.1523.
4. Halvorson HR, Vande Linde AMQ, Helpern JA, Welch KMA. Assessment of magnesium concentrations by 31P NMR in vivo. NMR Biomed. 1992;5:53–58 doi: 10.1002/nbm.1940050202.
5. Golding EM, Golding RM. Interpretation of 31P MRS Spectra in Determining Intracellular Free Magnesium and Potassium Ion Concentrations.; 1995.
6. Vanhamme L, Van Huffel S. AMARES: Advanced Method for Accurate, Robust and Efficient Spectral fitting of MRS data with use of prior knowledge. J. Magn. Reson. 1997;43:1–2.
7. Korzowski A, Weinfurtner N, Mueller S, et al. Volumetric mapping of intra- and extracellular pH in the human brain using 31P MRSI at 7T. Magn. Reson. Med. 2020;84:1707–1723 doi: 10.1002/mrm.28255.
Figures

Figure 1: Representative 31P spectra of model solutions from the chosen subset ([Na] = 29 mM, [K] = 160 mM) prepared with different pH values and ratios R = [Mg]/[ATP]. The spectra were acquired with a FID sequence with the following parameters: TR = 0.3 s, FA = 20°, bandwidth = 10kHz, 2048 spectral points, 1024 averages, Tmeas = 5 min. Spectral variation with changing pH is shown for fixed R = 0 (panel A), and also for changing R with fixed pH = 7.2 (panel B). Spectra are corrected for B0 shifts and zero- and first-order phases.
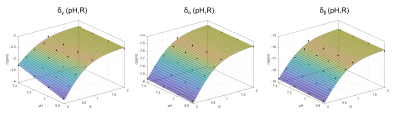
Figure 2: Visualization of the assumed relations δi(pH,R) described by Equation 1. The quantified chemical shifts δγ, δα, δβ from the spectra of the chosen subset are shown (black dots), as well as the corresponding fits of Equation 1 (colored surfaces). Deviations of the fit results from the data points are indicated as black pins.
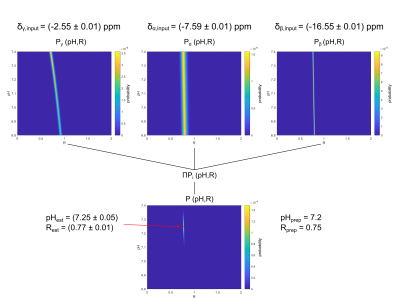
Figure 3: Estimation of pH for unknown R
based on the proposed dictionary approach for one specific example with
prepared conditions pHprep = 7.2 and Rprep = 0.75. The calculated
probability density functions Pi(pH,R) are shown for the individually
measured chemical shifts δγ,input = (-2.55 ± 0.01) ppm, δα,input = (-7.59 ± 0.01) ppm, and δβ,input = (-16.55 ± 0.01) ppm, as
well as the joined probability density function P(pH,R). The estimated values for
this example are pHest = 7.25 ± 0.05 and Rest = 0.77 ± 0.01.
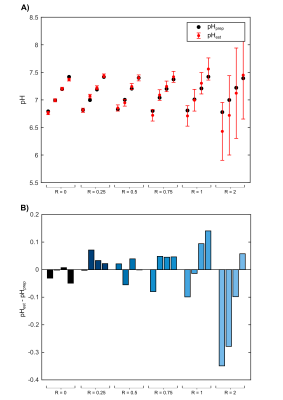
Figure 4: Performance of pH estimation via
the proposed dictionary-based approach for the entire chosen subset ([K] = 160 mM and [Na] = 29 mM). In panel A, estimated pH values (red dots) of all 24
model solutions of this subset are compared with the prepared values (black
dots). The results are grouped by Rprep of the model solutions.
Panel B shows the deviations of the estimated pH values from the prepared pH. With
increasing R, the estimated pH deviates stronger from the prepared pH.
DOI: https://doi.org/10.58530/2022/1364