Introduction

The two-compartment diffusion kurtosis imaging free water elimination model (DKI-FWE)¹ allows to mitigate the bias induced by partial volume effects on tissue-related diffusion parameters. The incorporation of the compartmental $$$T_2$$$ relaxation times helps stabilize the FWE model fitting problem². Therefore, accurate and precise parameter estimates can be obtained by using standard nonlinear least squares (NLLS) estimation techniques. However, DKI is a lengthy imaging protocol, implying that the choice of the data acquisition protocol plays a crucial role to achieve reliable quantifications of the tissue properties in competitive acquisition times. In this work, we optimize the diffusion weighting strengths ($$$b$$$-values) and echo times (TEs) in terms of the Cramér-Rao lower bound (CRLB) variances of the model parameters and derived metrics³.

Methods

DKI-FWE with explicit $$$T_2$$$-dependency (in short $$$T_2$$$-DKI-FWE) models the $$$T_2$$$ and diffusion weighted signal as: $$S = S_{00} \left( (1-f) \mathrm{exp}\left(-\mathrm{TE}/T_2^{\mathrm{tissue}}\right) S_{\mathrm{tissue}}(b, \mathbf{g};\boldsymbol{\theta}_{\mathrm{DKI}}) + f \mathrm{exp}\left({-\mathrm{TE}/T_2^{\mathrm{fw}}}\right) \mathrm{exp}(-bd) \right),$$ with $$$S_{00}$$$ the non-diffusion weighted signal at TE = 0 ms, $$$f$$$ the TE-independent free water signal fraction, $$$\mathbf{g}$$$ the diffusion weighting direction, $$$\boldsymbol{\theta}_{\mathrm{DKI}}$$$ the diffusion and kurtosis tensor parameter vector and $$$d$$$ the diffusivity of free water fixed to 3 μm²/ms. While $$$T_2^{\mathrm{tissue}}$$$ is estimated as an unknown model parameter, $$$T_2^{\mathrm{fw}}$$$ is fixed to a constant value of 1573 ms derived from literature⁴.
In this work, the acquisition schemes resulting from two different CRLB-based optimality criteria ($$$O_1$$$ and $$$O_2$$$) are compared with each other and with a reference scheme ($$$R$$$) consisting of four fixed $$$b$$$-values (0, 0.5, 1 and 2 ms/μm²) acquired at two different TEs (63 and 120 ms). The optimized scheme $$$O_1$$$, previously suggested by the authors⁵, was obtained by minimizing the sum of the CRLB variances of $$$\boldsymbol{\theta}_{\mathrm{DKI}}$$$, $$$f$$$ and the weighted CRLB variance of $$$T_2^{\mathrm{tissue}}$$$. In the current work, we assess an additional optimized protocol resulting from the minimization of the sum of the weighted CRLB variances of the fractional anisotropy (FA), mean diffusivity (MD), the linear part of the mean kurtosis ($$$\overline{K}_{app}^{*}$$$), $$$f$$$ and $$$T_2^{\mathrm{tissue}}$$$. In line with our previous work⁵, 120 uniformly distributed gradient directions were kept fixed during the optimization while $$$b$$$-values and TEs were free to vary in the range 0-2 ms/μm² and 63-121 ms, respectively. The optimality criteria were averaged over 500 white matter voxels with a certain degree of free water contamination ($$$0.05\leq f \leq 0.3$$$) and extracted from the $$$T_2$$$-DKI-FWE model fits of a real dataset. The weights applied in the optimization procedure were set equal to the inverse of the ground truth value of the parameter or metric of interest. The performance of all schemes was assessed both in terms of the maximum attainable precision (i.e. the CRLB) and the sample variances of relevant metrics (FA, MD, $$$\overline{K}_{app}^{*}$$$, $$$f$$$ and $$$T_2^{\mathrm{tissue}}$$$). The sample variances were evaluated in a single-voxel Monte Carlo simulation framework and an unconstrained NLLS fitting routine was used to prevent the introduction of any source of bias due to the position of constraints. In all experiments, Gaussian data distribution was assumed and the signal-to-noise ratio (SNR) was defined on the non-diffusion weighted signal of a non-free water contaminated voxel ($$$f$$$ = 0) at the lowest TE (i.e. 63 ms).

Results

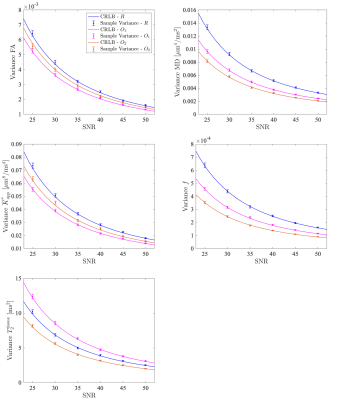
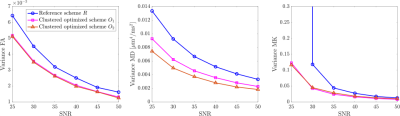
Figure 1 shows the distribution of the $$$b$$$-values and TEs for each acquisition scheme and a clustered version of the optimized schemes $$$O_1$$$ and $$$O_2$$$ is proposed for practical reasons. In Figure 2, the CRLB variances and the sample variances assessed in single-voxel experiments are compared for different metrics and for each scheme as a function of the SNR. Finally, in Figure 3, the sample variances of the FA, MD and mean kurtosis (MK) estimates are reported for the reference scheme $$$R$$$ and the clustered versions of $$$O_1$$$ and $$$O_2$$$.

Discussion

The good agreement between theoretical bounds and sample variances (Fig. 2) suggests that minimizing the CRLB variances of the parameters of interest is an appropriate criterion for optimal design. Our results highlight that, depending on the parameters included in the cost function and the weighting strategy, the precision of a specific set of metrics can be favored. As a proof of concept, we compare the schemes resulting from two different optimality criteria, $$$O_1$$$ and $$$O_2$$$. Both schemes outperform the conventional acquisition protocol $$$R$$$ in terms of the precision of FA, MD, $$$\overline{K}_{app}^{*}$$$ and $$$f$$$ in a range of medium/high SNR values. When comparing $$$O_1$$$ and $$$O_2$$$, it is clear that $$$O_2$$$ leads to a gain in precision for MD, $$$f$$$ and $$$T_2^{\mathrm{tissue}}$$$ while more precise FA and $$$\overline{K}_{app}^{*}$$$ estimates can still be achieved with $$$O_1$$$. Finally, clustering the optimal settings in fixed $$$b$$$-TE combinations does not affect the precision of the diffusion derived metrics (Fig. 3) and allows to set up a more practical acquisition.

Conclusion

This study shows that precise $$$T_2$$$-DKI-FWE parameter estimates can be achieved in reasonable acquisition times (< 10 minutes) by using CRLB-optimized settings. A validation of these findings on in vivo datasets will be subject of future work.

Acknowledgements

This project has received funding from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 764513. The work was also supported by the Research Foundation Flanders (FWO Belgium) through project funding (G084217N and 12M3119N).