1348

3D MR-STAT: towards a fast multi-parametric protocol with increased SNR
Hongyan Liu1, Oscar van den Heide1, Miha Fuderer1, Cornelis A.T. van den Berg1, and Alessandro Sbrizzi1
1Computational Imaging Group for MR diagnostics & therapy, Center for Image Sciences, UMC Utrecht, Utrecht, Netherlands

Synopsis

MR-STAT is a framework for simultaneous mapping of quantitative MR parameters from single short scans. In this work, we extend the current 2D Cartesian MR-STAT sequence to 3D acquisitions, in order to achieve higher SNR and isotropic resolution with a scan lasting few minutes. In particular, we implement a prototype 3D MR-STAT sequence for whole brain coverage with isotropic resolution, and test it on gel phantom and in-vivo brain data. Acceleration strategy of the 3D sequence is proposed, and the corresponding retrospective undersampling of the measured in-vivo data is reconstructed.

Introduction

MR-STAT is a framework for acquiring multi-parametric quantitative maps, such as T1, T2 and proton density from single short scans1. MR-STAT reconstruction iteratively solves a large scale, nonlinear optimization problem
$$\hat{\alpha}=\arg\min\frac{1}{2}||d-s(\alpha)||^2, (1)$$
where $$$d$$$ is the measured temporal domain data, $$$\alpha$$$ are all spatial parameter maps, and $$$s$$$ is the transient-state volumetric signal model. MR-STAT acquisitions usually use two-dimensional gradient-spoiled sequences with a smoothly varying flip-angle train and linear, Cartesian readouts2.
In this work, we extend the current 2D Cartesian MR-STAT sequence to 3D acquisitions, in order to achieve quantitative maps with increased SNR and isotropic resolution3,4. In particular, we implement a prototype 3D MR-STAT sequence with an FOV of 217 x 217 x 68mm^3 and 1.7mm^3 isotropic resolution, and present results on experimental gel phantom data and in-vivo brain data. To explore the possibility of reducing acquisition times, we also show reconstruction results leveraging parallel imaging techniques on retrospectively under-sampled 3D MR-STAT data. Results with an acceleration factor of 2 are presented, and higher acceleration factor will be investigated in the future. Our ultimate goal is to leverage these techniques to achieve high SNR 1mm^3 isotropic resolution maps in under 5 minutes.

Theory

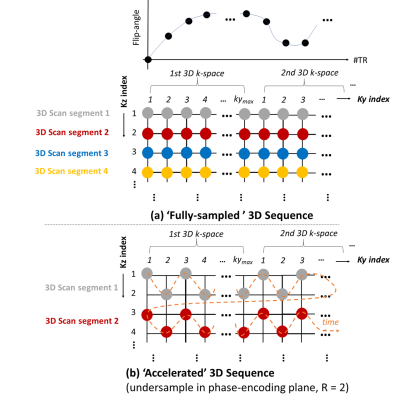
  • Sequence design
A typical 2D Cartesian MR-STAT sequence uses a smoothly varying flip-angle train with linear phase-encoding (ky) sampling. To cover a 3D volume, the multiple 2D MR-STAT sequence could be repeated for different slices (z locations). However, to increase SNR, we design a 3D Cartesian MR-STAT sequence. We achieve this by repeating the short 2D MR-STAT sequence as segments of the 3D sequence, each repetition corresponding to different kz phase-encoding lines, as shown in Fig.1(a).
In order to reduce the acquisition time, we also propose an acceleration strategy by undersampling data in the ky-kz phase-encoding plane, as shown in Fig.1(b). In this accelerated 3D sequence, we use the same 3D scan segment with linearly varying ky encoding lines as in the Fig.1(a), but with alternating kz encoding patterns. Note that the accelerated ky-kz phase encoding scheme resembles a 2D CAIPIRINHA pattern5.
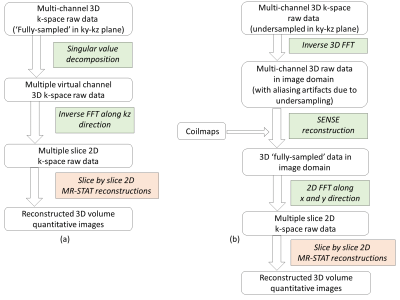
  • Reconstruction
Since MR-STAT reconstructions uses model-based iterative algorithms, running full 3D MR-STAT reconstructions can be very challenging in terms of memory requirements. In this work, we decouple the 3D MR-STAT data into independent 2D data subsets, such that fast 2D MR-STAT reconstruction algorithms can be applied6,7. For the 3D sequences shown in Fig.1(a), the 3D data can be decoupled into multiple 2D slices by inverse Fourier Transform along kz [Fig.2(a)]. For the accelerated sequences illustrated in Fig.1(b), the ‘undersampled’ 3D MR-STAT data are firstly transformed into image space, then a SENSE reconstruction is run to reconstruct ‘fully-sampled’ data in image domain. The SENSE reconstructed images are finally Fourier transformed to 2D kx-ky space, in order to run slice-by-slice 2D MR-STAT reconstructions [Fig.2(b)].

Method

  • Acquisition:
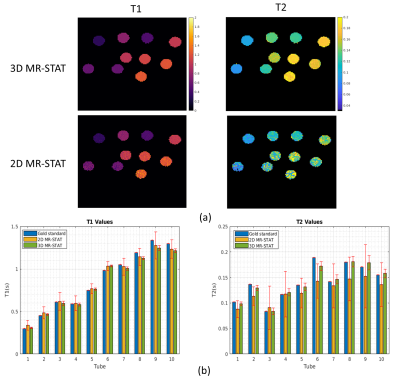
A 3D MR-STAT sequence as in Fig.1(a) was implemented on a 1.5T Philips Ingenia system (13-channel head-coil). The 3D sequence uses a short segment of 640 TRs with a smoothly varying flip-angle train8, and repeats it for all kz encoding lines. Each short segment starts with an adiabatic inversion pulse for better T1 encoding and ends with a 3-second waiting time for longitudinal signal recovery. Five 3D k-spaces are acquired in total. Other sequence parameters are: TE = 4.2ms, TR = 9.0 ms. The total scan time for this prototype sequence is about 7.4 minutes.
Both gel tube phantoms (Eurospin) and in-vivo brain (healthy volunteer) were scanned using the 3D MR-STAT sequence, as well as a multiple-2D MR-STAT sequence sharing the same scan parameters as the 3D segment for comparison. Inversion-recovery and single spin-echo experiments were performed on the gel phantoms to acquire the gold standard T1 and T2 values.
We also perform retrospective undersampling on the measured in-vivo data, with an acceleration factor of 2 in the ky-kz plane, which would reduce the required scan time to 3.7 minutes.
  • Reconstruction:
Reconstructions were run on an 8-Core desktop PC (3.7GHz CPU) using the decoupling strategy and the accelerated 2D MR-STAT algorithm6.

Results

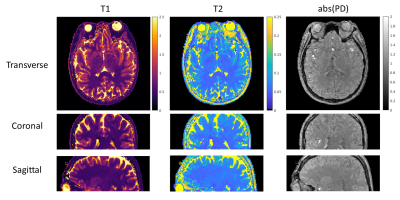
Fig.3 shows high agreements in T1 and T2 maps obtained from standard 3D MR-STAT data and gold standard data. 2D MR-STAT T2 maps are approximately 5 times noisier.
Fig.4 shows the quantitative maps of a human brain from the standard 3D MR-STAT scan in different views.
Fig.5 shows the reconstructed quantitative maps using retrospectively undersampled in-vivo data. Quantitative maps from the fully-sampled and undersampled sequence show no visible difference.
The total reconstruction time using the decoupled 2D reconstruction scheme is about 30 minutes.

Conclusion and Discussion

We demonstrated that extending 2D MR-STAT to 3D can be beneficial for acquiring isotropic quantitative maps with high quality. We show that data scanned by the prototype 3D sequence can be retrospectively undersampled by a factor of 2, and reconstructed following the proposed acceleration and reconstruction strategy. The total scan time will be further reduced by (a) reduce the current inefficient 3-second waiting times between 3D segments9 and (b) exploring higher acceleration rate or other undersampling strategy. Based on the framework we propose here, we aim at achieving whole brain coverage with 1mm^3 isotropic resolution in under 5 minutes by 3D MR-STAT in the future.

Acknowledgements

The first author receives CSC(Chinese Scholarship Counsel) scholarship.We would like to thank Niek R.F. Huttinga for helpful discussion on sequence design.

References

[1] Sbrizzi, Alessandro, et al. "Fast quantitative MRI as a nonlinear tomography problem." Magnetic resonance imaging 46 (2018): 56-63.

[2] van der Heide, Oscar, et al. "High‐resolution in vivo MR‐STAT using a matrix‐free and parallelized reconstruction algorithm." NMR in Biomedicine 33.4 (2020): e4251.

[3] Liao, Congyu, et al. "3D MR fingerprinting with accelerated stack-of-spirals and hybrid sliding-window and GRAPPA reconstruction." Neuroimage 162 (2017): 13-22.

[4] Chen, Yong, et al. "High-resolution 3D MR fingerprinting using parallel imaging and deep learning." Neuroimage 206 (2020): 116329.

[5] Breuer, Felix A., et al. "Controlled aliasing in volumetric parallel imaging (2D CAIPIRINHA)." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 55.3 (2006): 549-556.

[6] Liu, Hongyan, et al. “Accelerated MR-STAT Algorithm: Achieving 10-minute High-Resolution Reconstructions on a Desktop PC.” Proc. Intl. Soc. Mag. Reson. Med. 28 (2020), 3477.

[7] van der Heide, Oscar, Alessandro Sbrizzi, and Cornelis AT van den Berg. "Accelerated MR-STAT reconstructions using sparse Hessian approximations." IEEE Transactions on Medical Imaging 39.11 (2020): 3737-3748.

[8] Fuderer, Miha, et al. “BLAKJac - A computationally efficient noise-propagation performance metric for the analysis and optimization of MR-STAT sequences”. Proc. Intl. Soc. Mag. Reson. Med. 29 (2021), 3059.

[9] Amthor, Thomas, et al. "Magnetic resonance fingerprinting with short relaxation intervals." Magnetic resonance imaging 41 (2017): 22-28.

Figures

Fig.1. Example diagram of ‘fully-sampled’ and accelerated 3D Cartesian MR-STAT sequences. (a) A ‘fully-sampled’ 3D sequence with $$$kz_{max}$$$ segments, each scanning one kz encoding line. The ky-kz phase encoding plane is fully sampled $$$N_k$$$ times (usually $$$N_k$$$ = 5). (b) An accelerated 3D sequence with $$$kz_{max} / 2$$$ segments covering the same k-space as (a). The ky-kz phase encoding plane are undersampled with a factor of 2.

Fig.2. Flowchart of decoupling 3D MR-STAT data into 2D MR-STAT data using a standard 3D sequence (a) or an accelerated sequence (b). Low resolution coil-maps are used for decoupling data from the accelerated sequence.

Fig.3. Experimental gel phantom results from the prototype 3D MR-STAT scan. (a) T1 and T2 maps from 3D MR-STAT and 2D MR-STAT (central slice). (b) Mean values and standard deviations of T1 and T2 values in ten different phantom tubes obtained using 3D and 2D MR-STAT. Gold standard results are included for reference.

Fig.4. Experimental in-vivo results from the prototype 3D MR-STAT scan.

Fig.5. Reconstructed quantitative maps using data from (a) the prototype 3D MR-STAT scan (7.4 minutes) and (b) retrospectively undersampled data (3.7 minutes) by a factor of 2.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)
1348
DOI: https://doi.org/10.58530/2022/1348