Introduction

²³Na nuclei exhibit a quadrupolar moment and under certain conditions, one can observe besides the conventional single quantum coherences, also triple quantum (TQ) coherences. The TQ signal is very sensitive to its sodium environment¹ and could therefore provide additional information about the tissue and the state of the disease². Thus, further developments are warranted in ²³Na multi-quantum coherences (MQC) imaging. The ²³Na signal's intensity holds correlation with the ²³Na in-vivo concentration³ but suffers from poor SNR. In parallel, ¹H MRI offers superior SNR and fine morphological images with resolutions in the sub millimeter range but lacks access to tissue homeostasis information. Thus, we hypothesized that ¹H information can be utilized to enhance known tissue boundaries in ²³Na MRI⁴ to improve ²³Na MQC imaging.

Methods

Imaging was performed on 3T (phantom) and 7T (in-vivo) MRI (Trio and Magnetom, Siemens) with a 1Tx/Rx dual-tuned ¹H/²³Na head coil. Prior to the MQC scans, B0 shimming was repeated with a ¹H-based vendor provided 3D shimming routine until convergence. A home-built B1+ calibration sequence was employed to calibrate global 90° RF pulses. The optimal MQC evolution time τ was determined from a global TQTPPI spectroscopic prescan, followed by an offline fit.
Phantom: FoV 276x276x200mm³, matrix size 32x32x10 and TR=140ms resulting in a total of 62 minutes.
In-vivo: Three healthy volunteers were scanned to demonstrate in-vivo feasibility. 20 TEs, with TE₁=0.96ms (asymmetric echo, ΔTE=3ms), TR=390ms, phase increment Δφ=30° (12-steps phase cycle), matrix size 64x64, slice thickness 20mm, FOV=224mm and a bandwidth of 330Hz/Px, resulting in a total acquisition time of TA=50min. Anatomical information of the brain was obtained via multi-slice 2D ¹H TSE sequence with 1.2x1.2x3mm³, TE= 66ms, TR= 13.6s, BW= 224 Hz/px and TA=4:19 min.
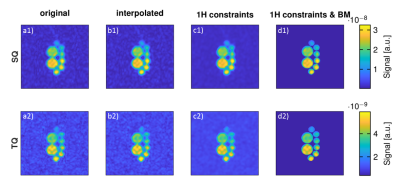
TQ and SQ images were reconstructed prior to data processing as described previously⁵. To match the resolution of the ¹H image and to ensure better image registration, ²³Na MQC data was interpolated to the same size as the ¹H image. Finally, interpolated ²³Na data were processed to limit partial volume effects with constraints from the ¹H prior first order total variation algorithm:
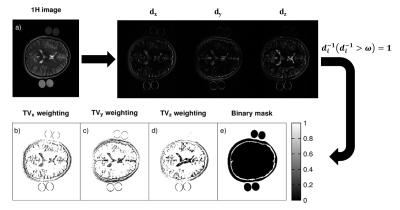
$$\underset{u}{{min}} \,\, \lambda_{xyz} ||\nabla_x u, \nabla_y u, \nabla_z u||_2 + \lambda_{BM} ||BM*u||_2 \ \, \,s.t. \, \, ||\varPhi_F (u) - f||^2_2 < \sigma^2 $$
With $$$u$$$ being the targeted improved interpolated image, $$$\varPhi_{F}$$$ indicating the partial Fourier transform and $$$f$$$ representing the measured data in frequency domain and $$$\sigma$$$ being the signal variance noise. ¹H prior information is used to detect sharp edges by calculating the first derivative along $$$x,y,z$$$ of the high resolution ¹H image. The derivatives are inverted and can be regarded as threshold maps to locally enhance edges and support TV denoising. The amount of included prior information can be controlled by setting a threshold, $$$ω$$$. $$$\lambda_{BM}||BM*u||_2$$$ represents another regularization term that penalizes the area outside of the region of interest, e.g. air in order to further reduce partial volume effects. $$$\lambda_{xyz}$$$ and $$$\lambda_{BM}$$$ are weighting parameters for the edge enhancing and the outer region penalizing regularization term, respectively. The Split-Bregman was utilized to solve the optimization problem stated in equation 1 with the following empirically determined weighting factors $$$\lambda_{xyz}=1$$$ and $$$\lambda_{BM}=0.4$$$. GPU computing was utilized resulting in a total reconstruction time of 140 seconds. To evaluate sharpness of an image, the sum of the absolute Wavelet coefficients (WAVS)⁶ was used. All calculations were performed in MATLAB (MATLAB R2020a, MathWorks, Natick, MA).

Results

Figure 1 demonstrates the ¹H TSE image and the computed thresholding maps to locally enhance and support TV denoising.
It is visible in Figure 2 that the proposed iterative reconstruction with ¹H prior constraints reduces partial volume effects.
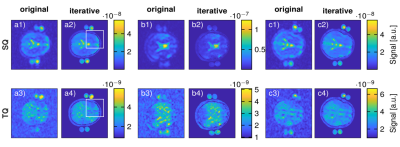
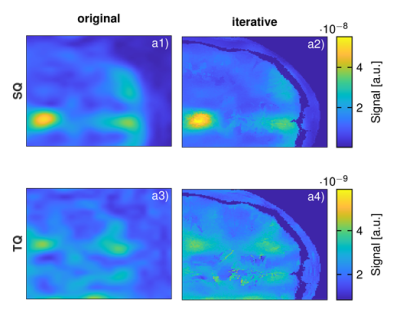
Figure 3 shows the comparison of regular ²³Na MQC and the proposed iterative reconstruction in-vivo. A clear distinction between the brain, the skull and the outer skin for all three volunteers is possible. Thus, the iterative reconstruction provides sharper images when compared to the standard reconstruction, WAVS_SQ=(1.07±0.37)*10^-4, WAVS_TQ = (5.59±1.54)*10^-4 , WAVS_SQiter=(1.12±0.26)*10^-3, WAVS_TQiter = (2.9±0.59)*10^-3.

Discussion

While the proposed framework enabled to reach virtual high resolution sodium MQC imaging, final images might locally appear grainy from the inherent noise in ¹H images. For instance in the mask, the cerebrospinal fluid exhibited speckles that could result in noise addition in the final ²³Na image. This could be alleviated with filtered ¹H images and/or the registration of all images in an atlas space.
Further processing could also include anatomical information from ¹H T1-weighted images or maps that identify specific regions such as white and gray matter to constrain their relative sodium intensity.
Fiege et. al.⁷ were not able to evaluate TQ information in large brain tumours due to limited MQC image resolution. The proposed iterative framework could complement TQ information as tumors, or other targeted lesion, could be well delineated in ¹H images.

Conclusion

We developed an iterative reconstruction algorithm that improves ²³Na MQC image quality by utilizing prior ¹H MR image information to preserve known tissue boundaries in Single and Triple Quantum sodium images.

Acknowledgements

No acknowledgement found.