1271
Improved spatial normalization of white matter fiber orientation distributions using T1-weighted contrast1Medical Physics, University of Wisconsin - Madison, Madison, WI, United States, 2Waisman Center, University of Wisconsin - Madison, Madison, WI, United States, 3Neuroscience Training Program, University of Wisconsin - Madison, Madison, WI, United States, 4Radiology, University of Wisconsin - Madison, Madison, WI, United States, 5Pediatrics, University of Wisconsin - Madison, Madison, WI, United States, 6Kinesiology Occupational Therapy Program, University of Wisconsin - Madison, Madison, WI, United States, 7Psychiatry, University of Wisconsin - Madison, Madison, WI, United States
Synopsis
Fiber orientation distributions (FOD) derived from diffusion magnetic resonance imaging (dMRI) enable resolution of multiple fiber populations within a voxel. FOD-based white matter studies include voxel-based analysis, atlas-based labeling, and group average fiber tracking. These methods require spatial normalization of the FODs. This work describes an alternative approach for FOD spatial normalization based on co-registering individual dMRI to the T1-weighted (T1w) images, non-linear spatial normalization of the T1w images to a template, and applying the transformations to the FOD maps. This approach is compared to the conventional approach of directly aligning FOD maps.
Introduction
Non-linear alignment of brain scans is frequently a necessary step in statistical analyses of quantitative magnetic resonance imaging studies (qMRI). In the case of white matter (WM) FOD-based analyses (FOD: fiber orientation distribution)1–3, WM-FOD maps derived from diffusion MRI (dMRI) are non-linearly warped to a standard template constructed from all or a subset of subjects in the study4. Here we present an alternative approach for intersubject alignment of WM-FOD maps that is based on linearly co-registering individual dMRI to accompanying T1-weighted (T1w) images, non-linearly warping the T1w images to a T1w template, then applying the resulting transformations to estimated WM-FOD maps. We show this alternative approach leads to reduced variability in WM-FOD-based parameters that can be attributed to improved intersubject alignment.Methods
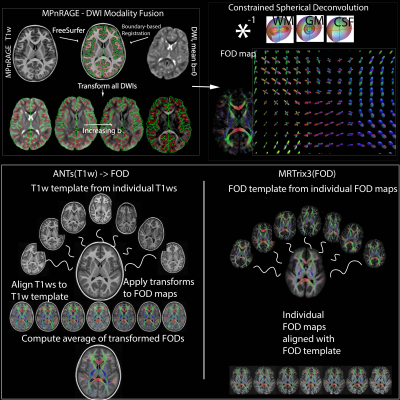
Data for 12 participants in an autism study were included in this work. dMRI data (9 directions at b=350 s·mm-2, 18 directions at 800 s·mm-2, 36 directions at b=2000 s·mm-2, 6 non-diffusion-weighted [b=0 s·mm-2, b0] volumes; isotropic 2.4mm resolution; 6 additional b0s with reverse phase-encoding direction collected for use in correcting susceptibility-induced artifacts) were pre-processed to minimize noise5,6, Gibbs ringing7, motion, eddy current8–10, and EPI distortion artifacts11. Structural T1w images (collected with the MPnRAGE12 sequence at 1mm isotropic resolution) were processed with the ‘recon-all’ FreeSurfer pipeline13 for estimating tissue boundaries and tissue labeling(Fig-1).The mean b0 and T1w were linearly co-registered (6 degrees of freedom) using boundary-based registration14(Fig-1). The estimated transformation was then applied to the entire dMRI series with cubic B-spline interpolation up-sampled to the T1-w resolution (1mm isotropic) using ANTs15. Finally, the rotational component of the rigid body transformation was applied to the dMRI encoding directions. Subsequently, dMRI data were spherically deconvolved with positivity constraints3 using estimated shell and tissue-specific response functions16(averaged across the participants) for estimating tissue-specific FODs at each voxel(Fig-1). Global intensity normalization in the log-domain was then performed on the three FOD maps using the ‘mtnormalise’ command in MRTrix317.
Inter-subject alignment of WM-FODs was conducted in two different ways. The conventional way using the MRTrix3 toolbox builds a WM-FOD template (‘population_template’ on the 12 participants with default settings) and non-linearly warps the individual WM-FOD maps to the template (‘mrregister’)4. An alternative approach using the ANTs toolbox builds a study-specific T1w template (using the ‘antsMultivariateTemplateConstruction’ script, 4 iterations)18–20, aligns the T1w images to the template, then applies the resulting transforms to the individual WM-FOD maps, and averages WM-FODs across subjects to generate a WM-FOD template that shares the same coordinate space as the T1w template. The approaches are labeled MRTrix3(FOD) and ANTs(T1w)->FOD respectively(Fig-1).
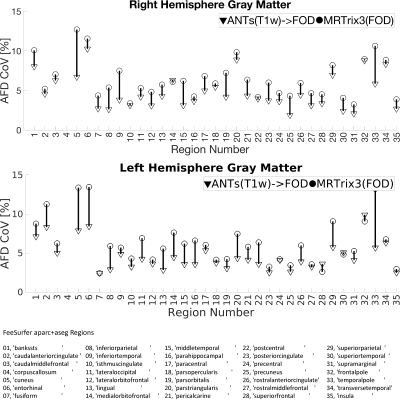
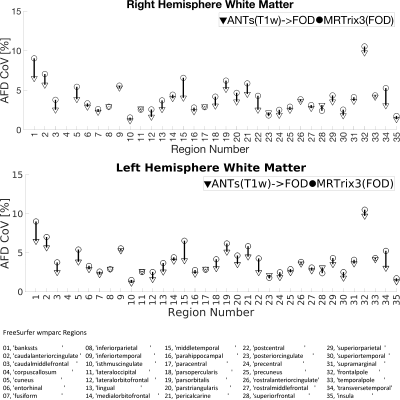
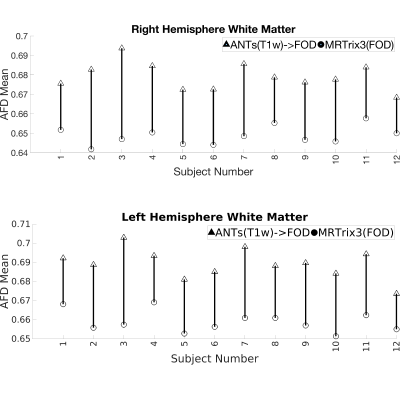
The quality of spatial alignment was judged visually and quantitatively. First, for each WM-FOD template, apparent fiber density21 (AFD) maps were computed as the first component (l=0) of the white matter FOD series scaled by 2√π. Then, cortical gray and white matter parcellations (35 regions each) obtained from FreeSurfer on individual T1w’s were mapped to each of the templates using the respective non-linear warps. Once mapped to a template, AFD was sampled in each region and averaged. This was done for each subject. Coefficient of variation (CoV) of the regional AFD was computed across subjects, so that lower CoV implies improved inter-subject regional alignment. In other words, for a given region, every participant is sampling from the same AFD template. Thus, the better the spatial inter-subject alignment the more likely it is for the same AFD voxels to be sampled across subjects resulting in lower CoV. Alternatively, regions-of-interest could be defined on the templates then mapped to and sample the native space AFD. However, it must then be ensured that those regions are anatomically consistent in both templates. Additionally, observed variability would be confounded by other factors such as neurobiological condition, age, etc. As we are sampling from the same template AFD map and the regions were defined the same in both cases, the observed variability can be attributed to the quality of alignment from each of the two approaches with more certainty.
Results
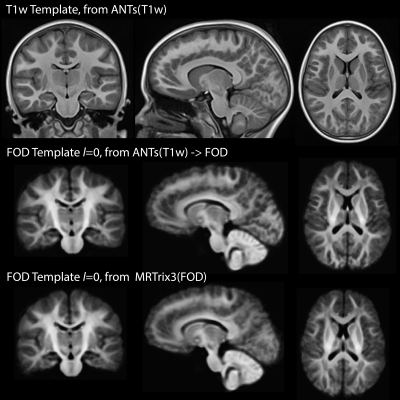
Visual inspection of Fig-2 reveals sharper tissue contrast in ANTs(T1w)->FOD compared MRTrix3(FOD). In regions such as the occipital lobe, cerebellum and more peripheral white matter the MRTrix3(FOD) template appears more blurred. This is consistent with better alignment of the individual WM-FOD maps in the ANTs(T1w)->FOD approach. Improved alignment with ANTs(T1w)->FOD may also be inferred from Figures 3 and 4. Most gray matter regions in Fig-3 show reduced CoV in the ANTs(T1w)->FOD compared to MRTrix3(FOD). This trend is also apparent for the white matter regions in Fig-4, but is less pronounced. Finally, in Fig-5 the sampled white matter AFD is higher in the case of ANTs(T1w)->FOD for all subjects. Lower AFD in the white matter could indicate more extensive degree of mixing of white and gray matter voxels during the template construction due to registration errors. Leading to a drop in the overall AFD, which is expected to be higher in white matter.Conclusion
The ANTs(T1w)->FOD normalization approach proposed in this work shows promise for reducing inter-subject variability in FOD-based analyses by decreasing image registration errors. Improved intersubject alignment of qMRI data should improve power in detecting differences or associations in analyses of diffusion neuroimaging studies.Acknowledgements
This work was supported by the Hartwell Foundation’s Individual Biomedical Award [to BT] and the National Institutes of Health [P30 HD003352, U54 HD090256, and P50 HD105353 to the Waisman Center, R01 HD094715 to BT and AL, and T32 CA009206 to the University of Wisconsin Radiological Sciences Training Program to JG]. NA is partially supported by NIH grants R01 NS111022, R01 NS117568, P01 AI132132, R01 AI138647, UF1AG051216, and R01 AG037639. DD is partially supported by NIH grants R00 MH11056. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.References
1. Tournier JD, Calamante F, Gadian DG, Connelly A. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. NeuroImage. 2004;23(3):1176-1185. doi:10.1016/j.neuroimage.2004.07.037
2. Tournier JD, Calamante F, Connelly A. Robust determination of the fibre orientation distribution in diffusion MRI: Non-negativity constrained super-resolved spherical deconvolution. NeuroImage. 2007;35(4):1459-1472. doi:10.1016/j.neuroimage.2007.02.016
3. Jeurissen B, Tournier JD, Dhollander T, Connelly A, Sijbers J. Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. NeuroImage. 2014;103:411-426. doi:10.1016/j.neuroimage.2014.07.061
4. Tournier JD, Smith R, Raffelt D, et al. MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation. NeuroImage. 2019;202:116137. doi:10.1016/j.neuroimage.2019.116137
5. Veraart J, Fieremans E, Novikov DS. Diffusion MRI noise mapping using random matrix theory: Diffusion MRI Noise Mapping. Magn Reson Med. 2016;76(5):1582-1593. doi:10.1002/mrm.26059
6. Veraart J, Novikov DS, Christiaens D, Ades-aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. NeuroImage. 2016;142:394-406. doi:10.1016/j.neuroimage.2016.08.016
7. Kellner E, Dhital B, Kiselev VG, Reisert M. Gibbs-ringing artifact removal based on local subvoxel-shifts: Gibbs-Ringing Artifact Removal. Magn Reson Med. 2016;76(5):1574-1581. doi:10.1002/mrm.26054
8. Andersson JLR, Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage. 2016;125:1063-1078. doi:10.1016/j.neuroimage.2015.10.019
9. Andersson JLR, Graham MS, Drobnjak I, Zhang H, Filippini N, Bastiani M. Towards a comprehensive framework for movement and distortion correction of diffusion MR images: Within volume movement. NeuroImage. 2017;152:450-466. doi:10.1016/j.neuroimage.2017.02.085
10. Andersson JLR, Graham MS, Zsoldos E, Sotiropoulos SN. Incorporating outlier detection and replacement into a non-parametric framework for movement and distortion correction of diffusion MR images. NeuroImage. 2016;141:556-572. doi:10.1016/j.neuroimage.2016.06.058
11. Andersson JLR, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage. 2003;20(2):870-888. doi:10.1016/S1053-8119(03)00336-7
12. Kecskemeti S, Samsonov A, Hurley SA, Dean DC, Field A, Alexander AL. MPnRAGE: A technique to simultaneously acquire hundreds of differently contrasted MPRAGE images with applications to quantitative T 1 mapping. Magn Reson Med. 2016;75(3):1040-1053. doi:10.1002/mrm.25674
13. Dale AM, Fischl B, Sereno MI. Cortical Surface-Based Analysis. NeuroImage. 1999;9(2):179-194. doi:10.1006/nimg.1998.0395
14. Greve DN, Fischl B. Accurate and robust brain image alignment using boundary-based registration. NeuroImage. 2009;48(1):63-72. doi:10.1016/j.neuroimage.2009.06.060
15. Avants BB, Tustison NJ, Song G, Cook PA, Klein A, Gee JC. A reproducible evaluation of ANTs similarity metric performance in brain image registration. NeuroImage. 2011;54(3):2033-2044. doi:10.1016/j.neuroimage.2010.09.025
16. Dhollander T, Raffelt D, Connelly A. Unsupervised 3-tissue response function estimation from single-shell or multi-shell diffusion MR data without a co-registered T1 image. In: ; 2016.
17. Dhollander T, Tabbara R, Rosnarho-Tornstrand J, Tournier J, Raffelt D, Connelly A. Multi-tissue log-domain intensity and inhomogeneity normalisation for quantitative apparent fibre density. In: ; 2021.
18. Avants BB, Yushkevich P, Pluta J, et al. The optimal template effect in hippocampus studies of diseased populations. NeuroImage. 2010;49(3):2457-2466. doi:10.1016/j.neuroimage.2009.09.062
19. Klein A, Ghosh SS, Avants B, et al. Evaluation of volume-based and surface-based brain image registration methods. NeuroImage. 2010;51(1):214-220. doi:10.1016/j.neuroimage.2010.01.091
20. Avants BB, Tustison NJ, Song G, Cook PA, Klein A, Gee JC. A reproducible evaluation of ANTs similarity metric performance in brain image registration. NeuroImage. 2011;54(3):2033-2044. doi:10.1016/j.neuroimage.2010.09.025
21. Raffelt D, Tournier JD, Rose S, et al. Apparent Fibre Density: A novel measure for the analysis of diffusion-weighted magnetic resonance images. NeuroImage. 2012;59(4):3976-3994. doi:10.1016/j.neuroimage.2011.10.045
Figures