1171
Flip-angle map calculation via keyhole reconstruction in uniform and variable-density 2D-spiral hyperpolarized 129Xe MRI1Center for Pulmonary Imaging Research, Department of Pulmonary Medicine, Cincinnati Children's Hospital Medical Center, Cincinnati, OH, United States, 2Biomedical Engineering, University of Cincinnati, Cincinnati, OH, United States, 3Department of Radiology, Cincinnati Children's Hospital Medical Center, Cincinnati, OH, United States, 4Department of Pediatrics, Cincinnati Children's Hospital Medical Center, Cincinnati, OH, United States
Synopsis
Hyperpolarized 129Xe-MRI is prone to B1-inhomogeneity-induced signal artifacts, that often obscure pulmonary abnormalities. B1-inhomeogeneity can be corrected by calculating a flip-angle map and rescaling the images. Current methods to acquire a flip-angle map in 2D-spiral sequences require two-successive images to be collected in a single breath-hold, doubling scan duration. We demonstrate that flip-angle maps can be calculated from a single image acquisition using keyhole reconstruction. Furthermore, analytical methods can be used to minimize the amount of required oversampling. This approach enables accurate B1-artifact correction, with minimal impact to scan-duration, making it especially useful for short breath-hold studies.
Introduction
Hyperpolarized 129Xe-MRI is a powerful imaging technique, most-well known for its ability to characterize regional gas-uptake and airway-obstruction in the lungs from a single breath-hold image1-3. Its feasibility is particularly benefitted by center-out sequences, such as 2D-spiral, where sampling-efficiency and scan-duration, and thus breath-hold duration, are improved. However, 129Xe-MRI is highly sensitive to regional differences in applied flip-angle caused by B1-field inhomogeneity. This may cause signal artifacts that obscure pulmonary abnormalities, including ventilation deficits, and therefore require correction.An accurate means to correct for B1-variations is to measure a flip-angle map, and retrospectively rescale the acquired image. When acquisition-time is much less than the in-vivo T1 (~20s)4, flip-angle maps can be generated by acquiring two images within the same breath-hold, and calculating signal decay between them5. While this ‘paired-image’ approach produces accurate flip-angle maps, it doubles the scan-duration – increasing the length and difficulty of the breath-hold maneuver. Here, we propose using keyhole-reconstruction combined with either uniform or variable-density 2D-spiral sequences to generate the two images from a single-image acquisition6,7.
Theory
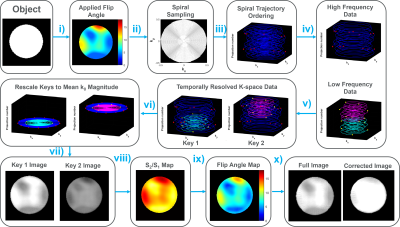
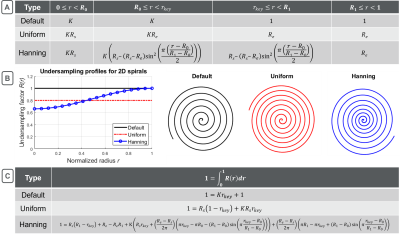
In keyhole-reconstruction, dynamic low-frequency k-space data is divided into K ‘keys’ and combined with the high-frequency k-space data (‘keyhole’) to generate K key-images (K=2 for this work). Voxel-by-voxel signal decay between key-images can be used to calculate a flip-angle map (Fig. 1). The level of spatial detail that can be resolved in the flip-angle map is controlled by the key-radius, rkey. To prevent aliasing artifacts that arise from Nyquist-undersampling inside the key, the 2D-spiral sequence must be oversampled. The degree of oversampling depends on the shape, direction, and sampling-density of the trajectories, and the post-processing details: rkey, and K. A general equation for the degree of oversampling required is given by:$$1 = \int_{0}^{1} R(r) \,dr, \tag{1}$$
where R(r) is the undersample factor of an Archimedean spiral at normalized radial-position, r, from the center of k-space. A fully-sampled spiral sequence has R=1, an oversampled uniform spiral sequence has R<1, and a variable-density spiral sequence has non-constant R(r) (Fig. 2(A,B)). The division of low-frequency k-space into K keys means that R(r) can be represented as piecewise function from the center of k-space, to rkey, to the edge of k-space. Once a sufficient rkey is chosen, Eq. 1 can be solved to determine the required oversampling profile (Fig. 2(C)).
Methods
Simulations were performed in MATLAB (Mathworks, Natick, MA), using a digital-phantom with a spatially varying applied flip-angle (Figs. 1&2). Matrix=2002, spiral-interleaves=100, K=2, rkey=0.1-0.9, R=0.9, uniform-density spiral-out. Calculated flip-angle maps were compared against the applied map using the voxel root-mean square-difference, μdiff2, and the variance difference, σdiff2.Imaging was performed on a Philips-Achieva 3T scanner, with hyperpolarized-129Xe (25-35% polarization8, via Polarean 9820A, Durham, NC). Scans were performed on 129Xe-gas phantoms (1-L Tedlar bag) and in-vivo (healthy male, 30years and cystic-fibrosis female, 21years), under protocol approved by our local Institutional Review Board (with FDA IND-123,577). Imaging parameters: Field-of-view (FOV)=(350-400)x(350-400)x200mm3, resolution=3x3x15mm3, acquisition-time=5ms, echo-time=1.52ms, repetition-time=11.0ms, spiral-interleaves=13-29, flip-angles=9-18⁰. Images were reconstructed using open-source non-cartesian software9.
Results
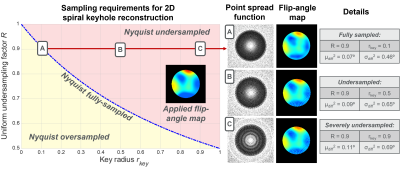
Nyquist-undersampling effects that occur by not meeting Eq. 1 are shown using simulations in Fig. 3. Alias-free flip-angle map reconstructions were achieved using rkey=0.1, with R=0.9 applied uniform-oversampling (μdiff2=0.07⁰, σdiff2=0.46⁰) (Fig. 3(A)). Figs. 3(B,C) show reconstructions for the same R, but rkey=0.5 and rkey=0.9. Here, aliasing artifacts are generated within the supported-FOV of the point-spread-functions, and the accuracy of the flip-angle maps decreased, respectively: μdiff2=0.09⁰, σdiff2=0.65⁰, and μdiff2=0.11⁰, σdiff2=0.69⁰.The effects of reconstructing with various rkey are shown in Fig. 4. Optimal flip-angle maps were obtained using the largest rkey: rkey=0.5, R=0.67, at a scan-duration of t=4.25s (μdiff2=0.02⁰, σdiff2=0.61⁰ against the paired-image flip-angle map). Shorter scan-durations were possible with rkey=0.25, R=0.8, t=3.6s and rkey=0.1, R=0.91, t=3.1s; however, these flip-angle maps were less accurate (μdiff2=0.06⁰, σdiff2=0.93⁰, and μdiff2=0.08⁰, σdiff2=1.34⁰, respectively).
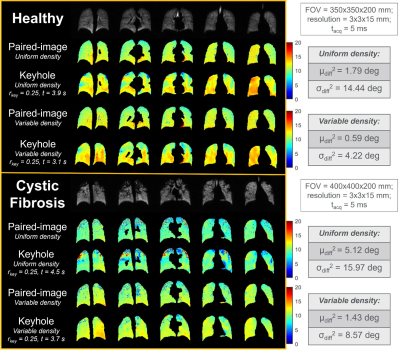
Uniform and variable-density (via Hanning-window) 2D-spiral images were collected in-vivo to test keyhole-reconstruction (Fig. 5). Comparisons between the keyhole and paired-image generated flip-angle maps gave: healthy uniform: μdiff2=1.79⁰, σdiff2=14.44⁰; variable-density: μdiff2=0.59⁰, σdiff2=4.22⁰; cystic-fibrosis uniform: μdiff2=5.12⁰, σdiff2=15.97⁰; variable-density: μdiff2=1.43⁰, σdiff2=8.57⁰. Variable-density spirals had ~3-fold greater accuracy and ~20% shorter scan-durations than uniform spirals.
Discussion
In general, keyhole-reconstructions produced spatially similar flip-angle maps to the paired-image approach. Notably, reconstructions with a larger key-radius delivered greater accuracy. However, these required a greater degree of initial oversampling to prevent Nyquist-undersampling artifacts from propagating into the flip-angle map. In turn, this increased the scan-duration. To minimize scan-duration and prevent map artifacts, the key-radius must be balanced with the amount of initial oversampling.Accuracy and scan-duration was enhanced by using variable-density spirals, with increased density at center. This was more efficient for keyhole-reconstruction, as only the central k-space information needed oversampling to avoid aliasing in the key-images. Consequently, scan-durations were shortened by >20%, and accuracy was improved ~3-fold, when compared to uniform-density spirals.
Conclusion
Keyhole-reconstruction can be used to calculate accurate flip-angle maps from a single 2D-spiral image-acquisition. Such maps are generated with minimal impact to scan-duration and can be optimized further for various sequence parameters. This is especially useful in 129Xe-MRI studies where short scan-durations are necessary, such as for children and patients with compromised respiratory-function. This work can be used to apply corrections for B1-inhomogeneity, with minimal impact to scan-duration.Acknowledgements
The authors would like to thank Dustin J. Basler for polarizing 129Xe for this study. Additionally, we would like to thank the following sources for research funding and support: R01HL131012 and R01HL143011.References
1. Walkup, L.L. and J.C. Woods, Translational applications of hyperpolarized 3He and 129Xe. NMR Biomedicine, 2014. 27(12): p. 1429-38.
2. Bdaiwi, A.S., et al., Improving hyperpolarized 129Xe ADC mapping in pediatric and adult lungs with uncertainty propagation. NMR Biomedicine, 2021: p. e4639.
3. Niedbalski, P.J., et al., Protocols for multi-site trials using hyperpolarized 129Xe MRI for imaging of ventilation, alveolar-airspace size, and gas exchange: A position paper from the 129Xe MRI clinical trials consortium. Magnetic Resonance in Medicine, 2021. 86(6): p. 2966-2986.
4. Mugler, J.P. and T.A. Altes, Hyperpolarized 129Xe MRI of the human lung. Journal Magnetic Resonance Imaging, 2013. 37(2): p. 313-31.
5. Miller, G.W., et al., Hyperpolarized 3He lung ventilation imaging with B1-inhomogeneity correction in a single breath-hold scan. Magma, 2004. 16(5): p. 218-26.
6. Niedbalski, P.J. and Z.I. Cleveland, Improved preclinical hyperpolarized 129Xe ventilation imaging with constant flip angle 3D radial golden means acquisition and keyhole reconstruction. NMR Biomedicine, 2021. 34(3): p. e4464.
7. Niedbalski, P.J., et al., Mapping and correcting hyperpolarized magnetization decay with radial keyhole imaging. Magnetic Resonance Medicine, 2019. 82(1): p. 367-376.
8. Plummer, J.W., et al., A semi-empirical model to optimize continuous-flow hyperpolarized 129Xe production under practical cryogenic-accumulation conditions. Journal of Magnetic Resonance, 2020. 320: p. 106845.
9. Robertson, S.H., et al., Optimizing 3D non-cartesian gridding reconstruction for hyperpolarized 129Xe MRI—focus on preclinical applications. Concepts in Magnetic Resonance Part A, 2015. 44(4): p. 190-202.
Figures