1170
129Xe MRI Binning Analysis using Reference Values: Age-dependent Changes in Gas-Exchange MRI1Pulmonary Medicine, Cincinnati Children's Hospital Medical Center, Cincinnati, OH, United States, 2Biomedical Engineering, University of Cincinnati, Cincinnati, OH, United States, 3Radiology, Cincinnati Children's Hospital Medical Center, Cincinnati, OH, United States, 4Pediatrics, University of Cincinnati Medical Center, Cincinnati, OH, United States, 5Physics, University of Cincinnati, Cincinnati, OH, United States
Synopsis
Previous 129Xe-MRI binning analysis techniques assumed normal distributions or relied on a Box-Cox transformation. Adapting these binning methods to account for known covariates of lung function and structure, such as age and height, was not straightforward. To account for these limitations, a new binning method is proposed here that uses the same modeling techniques used to increase sensitivity and specificity in spirometry and diffusing capacity for carbon monoxide (DLCO). By accounting for MRI image distribution shapes and covariates, healthy representative data distributions are better modelled and can permit increased sensitivity and specificity, particularly for early cardiopulmonary disease progression.
Introduction:
Hyperpolarized 129Xe-MRI has proven to be a sensitive tool to monitor and spatially resolve regional ventilation, alveolar-airspace size, and gas-exchange1–5. Many studies implement a linear-binning technique to extract sensitive quantitative measures6–9. The linear-binning technique fits a normal distribution to a healthy-reference cohort, and thresholds defining abnormal function are derived relative to standard deviations from the healthy reference mean. A generalized linear-binning technique was later proposed, which uses the Box-Cox transformation to/from a normal distribution, where the initial linear-binning method can be implemented.However, there are well documented differences in lung function and structure associated with sex and age10–14. Normative reference equations for pulmonary-function testing, like those from the Global Lung Initiative (GLI), adjust predictive values based on these covariates to improve sensitivity/specificity while enabling more rigorous comparisons across subjects from various demographics10,11. To accomplish this, the GLI used a modern distribution-based approach to semiparametric regression. Here, we implement a similar method using this regression technique to determine binning thresholds and demonstrate it by applying it to healthy 129Xe gas-exchange MRI.
Methods:
22 healthy subjects were imaged according to a protocol approved by our local Institutional Review Board (with FDA IND-123,577). 129Xe (86%-enriched) was polarized to 30-40% via a 129Xe hyperpolarizer (Polarean 9820A, Durham, NC). Subjects were recruited to cover a wide range of ages and from both sexes (Figure 1).129Xe gas-exchange MRI was acquired on Philips 3.0T scanners using a commercial or custom-built dual-loop 129Xe coil. Subjects inhaled a volume of 129Xe equivalent to 1/6th of their height-predicted total lung capacity up to 1 liter15. 129Xe gas-exchange MRI was acquired during a 15-second breath hold via the 1-point Dixon method and RF-excitation at 202ppm8,16, with reconstruction using published methods16,17. Ventilation images were corrected for coil inhomogeneity using N4-bias correction and normalized to the 99th percentile7,18. Barrier-uptake and RBC-transfer maps were calculated by dividing barrier and RBC images by the gas-phase image, while RBC:barrier maps were calculated by dividing the RBC image by the barrier image.
To accurately represent healthy-reference distributions, 2,000 lung voxels were randomly selected from each subject. The healthy-reference distributions were fit as a function of age, using the Box-Cox power exponential (BCPE) distribution within the GAMLSS (Generalized Additive Models for Location, Scale and Shape) software package in R19,20. The BCPE distribution is defined by four variables: median, coefficient of variation, skewness, and kurtosis. Optimal models were determined by minimizing the global-deviance with a generalized Akaike information criterion penalization21. A penalty of 3.84 per degree of freedom (Chi-squared test with one degree of freedom) was chosen over default penalty of 2 to reduce chance of overfitting19. Five binning thresholds (6 bins) were determined for each gas-exchange measurement via Z-scores of -2, -1, 0, 1, and 2 (percentiles ≈ 2.28, 15.87, 50.00, 84.13, and 97.72). This proposed model (LSS-binning, Location, Scale, and Shape) was compared to the linear-binning method.
Results:
In Figure 2, LSS-binning shows most of the healthy-cohort distribution parameters vary with age. Furthermore, the BCPE skew and kurtosis parameter distributions are not equal to 1 and 2, respectively, so a normal distribution cannot be assumed. The distribution medians vary ~4-11% over this age range (ventilation, 4.0%; RBC:barrier, 4.2%; RBC-transfer, 10.9%; barrier-uptake, 11.0%). The coefficient of variation also exhibits large variance with age (up to ~30%). Using these distribution parameters, Z-scores (equivalent to standard-deviation thresholds for a normal distribution), obtained as a function of age, provide the LSS-thresholds (Figure 3).Comparisons between reference distributions for linear-binning and LSS-binning show large differences. Distributions for linear- and LSS-binning methods are shown in Figure 4. By using age-dependent thresholds, via LSS-binning, the binning maps and percentages shift closer to the expected distribution of voxels for healthy subjects (15.9%, Figure 5). Additionally, the percent of data falling outside of bins 3 and 4 increases using LSS-binning, indicative of narrower thresholds.
Discussion:
The LSS-binning method enables binning of Xe gas-exchange MRI images using thresholds dependent on age. This results in age-dependent Xe MRI reference distributions, which is expected, considering age is a significant covariate in pulmonary function tests. By considering age-dependent median-signal intensities, the coefficient of variation can be reduced for all measurements, narrowing the reference distributions (some being age-dependent).Since LSS-binning accounts the location, shape, and scale of the distribution with respect to age, the variation in the percentage of voxels in each bin would be diminished, reducing the upper limit of normal in defect and high bins. An alternative approach could be to model bin percentages but would make binning maps less useful. In practice, the narrower healthy reference distributions should increase sensitivity to early disease.
Conclusion:
An extension to linear-binning, LSS-binning, can better account for Xe MRI image distributions and covariates, such as age. Applying LSS-binning to Xe gas-exchange MRI demonstrates age-dependent healthy reference distributions, which permits a more sensitive analysis of lung function. More subjects will be necessary to obtain more accurate thresholds as a function of age and to consider other covariates such as sex and height.Acknowledgements
The authors would like to thank Drs. Bastiaan Driehuys, David G. Mummy, and Elianna A. Bier for initial discussions on this topic. Additionally, we would like to thank the following sources for research funding and support: Cincinnati Children’s Research Foundation (Trustee Award, Walkup), R01HL151588, R01HL143011, R01HL146689, and CFFWOODS19A0.
References
1. Wang Z, Rankine L, Bier EA, et al. Using hyperpolarized 129Xe gas-exchange MRI to model the regional airspace, membrane, and capillary contributions to diffusing capacity. J Appl Physiol. 2021;130(5):1398-1409. doi:10.1152/japplphysiol.00702.2020
2. Rayment JH, Couch MJ, McDonald N, et al. Hyperpolarised 129Xe magnetic resonance imaging to monitor treatment response in children with cystic fibrosis. Eur Respir J. 2019;53(5). doi:10.1183/13993003.02188-2018
3. Virgincar RS, Cleveland ZI, Sivaram Kaushik S, et al. Quantitative analysis of hyperpolarized 129Xe ventilation imaging in healthy volunteers and subjects with chronic obstructive pulmonary disease. NMR Biomed. 2013;26(4):424-435. doi:10.1002/nbm.2880
4. Qing K, Mugler JP, Altes TA, et al. Assessment of lung function in asthma and COPD using hyperpolarized 129Xe chemical shift saturation recovery spectroscopy and dissolved-phase MRI. NMR Biomed. 2014;27(12):1490-1501. doi:10.1002/nbm.3179
5. Couch MJ, Thomen R, Kanhere N, et al. A two-center analysis of hyperpolarized 129Xe lung MRI in stable pediatric cystic fibrosis: Potential as a biomarker for multi-site trials. J Cyst Fibros. 2019;18(5):728-733. doi:10.1016/j.jcf.2019.03.005
6. He M, Wang Z, Rankine L, et al. Generalized Linear Binning to Compare Hyperpolarized 129Xe Ventilation Maps Derived from 3D Radial Gas Exchange Versus Dedicated Multislice Gradient Echo MRI. Acad Radiol. 2020;27(8):e193-e203. doi:10.1016/j.acra.2019.10.016
7. Wang Z, Robertson SH, Wang J, et al. Quantitative analysis of hyperpolarized 129Xe gas transfer MRI. Med Phys. 2017;44(6):2415-2428. doi:10.1002/mp.12264
8. Wang Z, He M, Bier E, et al. Hyperpolarized 129Xe gas transfer MRI: the transition from 1.5T to 3T. Magn Reson Med. 2018;80(6):2374-2383. doi:10.1002/mrm.27377
9. He M, Kaushik SS, Robertson SH, et al. Extending Semiautomatic Ventilation Defect Analysis for Hyperpolarized 129Xe Ventilation MRI. Acad Radiol. 2014;21(12):1530-1541. doi:10.1016/j.acra.2014.07.017
10. Stanojevic S, Wade A, Stocks J, et al. Reference ranges for spirometry across all ages: A new approach. Am J Respir Crit Care Med. 2008;177(3):253-260. doi:10.1164/rccm.200708-1248OC
11. Stanojevic S, Graham BL, Cooper BG, et al. Official ERS technical standards: Global Lung Function Initiative reference values for the carbon monoxide transfer factor for Caucasians. Eur Respir J. 2017;50(3). doi:10.1183/13993003.00010-2017
12. Zeman KL, Bennett WD. Growth of the small airways and alveoli from childhood to the adult lung measured by aerosol-derived airway morphometry. J Appl Physiol. 2006;100(3):965-971. doi:10.1152/japplphysiol.00409.2005
13. de Jong PA, Long FR, Wong JC, et al. Computed tomographic estimation of lung dimensions throughout the growth period. Eur Respir J. 2006;27(2):261-267. doi:10.1183/09031936.06.00070805
14. Gevenois PA, Scillia P, de Maertelaer V, Michils A, De Vuyst P, Yernault JC. The effects of age, sex, lung size, and hyperinflation on CT lung densitometry. Am J Roentgenol. 1996;167(5):1169-1173. doi:10.2214/ajr.167.5.8911175
15. Stocks J, Quanjer PH. Reference values for residual volume, functional residual capacity and total lung capacity: ATS Workshop on Lung Volume Measurements Official Statement of the European Respiratory Society. Eur Respir J. 1995;8(3):492-506. doi:10.1183/09031936.95.08030492
16. Willmering MM, Cleveland ZI, Walkup LL, Woods JC. Removal of off-resonance xenon gas artifacts in pulmonary gas-transfer MRI. Magn Reson Med. 2021;86(2):907-915. doi:10.1002/mrm.28737
17. Robertson SH, Virgincar RS, He M, Freeman MS, Kaushik SS, Driehuys B. Optimizing 3D noncartesian gridding reconstruction for hyperpolarized 129Xe MRI-focus on preclinical applications. Concepts Magn Reson Part A Bridg Educ Res. 2015;44(4):190-202. doi:10.1002/cmr.a.21352
18. Tustison NJ, Avants BB, Cook PA, et al. N4ITK: Improved N3 Bias Correction. IEEE Trans Med Imaging. 2010;29(6):1310-1320. doi:10.1109/TMI.2010.2046908
19. Rigby RA, Stasinopoulos DM, Lane PW. Generalized additive models for location, scale and shape. J R Stat Soc Ser C Appl Stat. 2005;54(3):507-554. doi:10.1111/j.1467-9876.2005.00510.x
20. Rigby RA, Stasinopoulos DM. Smooth centile curves for skew and kurtotic data modelled using the Box-Cox power exponential distribution. Stat Med. 2004;23(19):3053-3076. doi:10.1002/sim.1861
21. Cavanaugh JE. Unifying the derivations for the Akaike and corrected Akaike information criteria. Stat Probab Lett. 1997;33(2):201-208. doi:10.1016/s0167-7152(96)00128-9
Figures
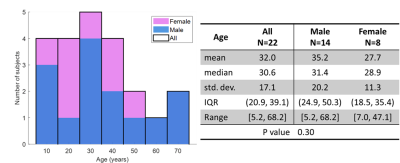
Figure 1: Distribution characteristics for age and gender of the 22 healthy subjects used in this study. Left, histogram of ages with sex shown as different colors. P value indicates there is no significant difference in age distributions between the sexes (two-sided t-test, unequal variances).
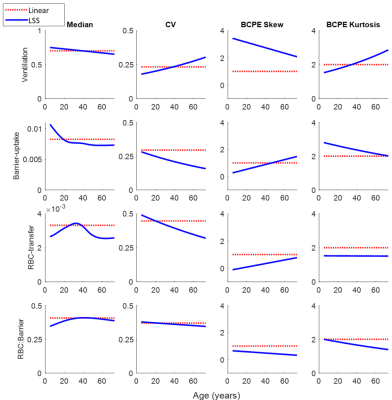
Figure 2: The fitted distribution parameters for the linear-binning and LSS-binning methods. Median, coefficient of variation (CV), skew, and kurtosis are shown for the four main gas-exchange metrics, ventilation, barrier-uptake, RBC-transfer, and RBC:barrier ratio. Skew and kurtosis were defined using the BCPE definition (1 and 2 for a normal distribution, respectively).
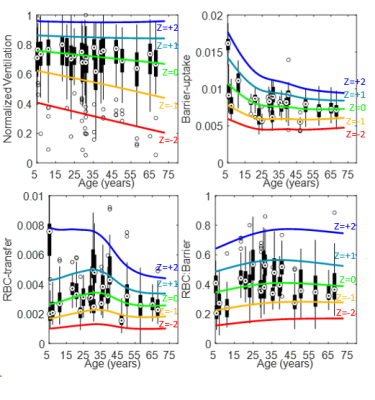
Figure 3: LSS-binning Z-score thresholds, as a function of age for the ventilation, barrier-uptake, RBC-transfer, and RBC:barrier parameters. The thresholds, Z = -2 to 2 in increments of 1, overlay box plots of each subject’s distribution. The circle target within the box represents the median intensity, the box indicates 25th-75th percentiles, the whiskers represent the range (ignoring outliers), and empty circles represent outliers (intensity > ±1.5 times inter-quartile range).
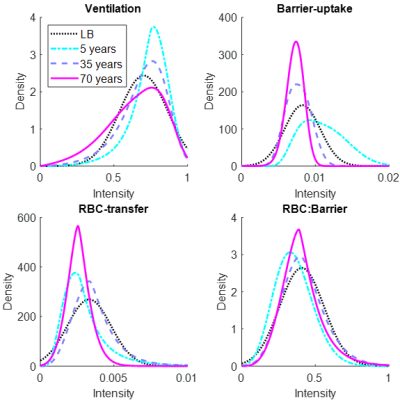
Figure 4: Example healthy distributions using the linear-binning and LSS-binning methods. Three ages for the LSS-binning method are shown (5 years old (blue), 35 years old (purple), and 70 years old (pink)). The linear-binning method often results in broader distributions than LSS-binning. Additionally, the median often shifts as a function of age.
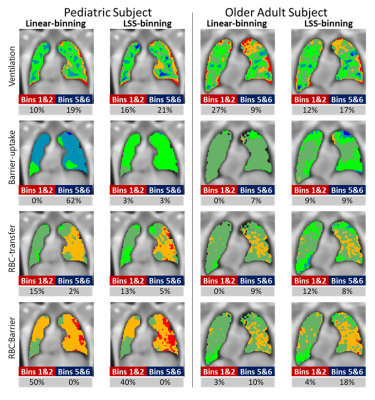
Figure 5: Example binned images for an 11-year-old and 68-year-old subject using the linear- and LSS-binning approaches. Colors indicate the bin where bins 1 and 2 are red and orange, bins 3 and 4 are green, and bins 5 and 6 are blues. For each metric and method, the percent of voxels which have a Z-score less than -1 (Bins 1 and 2) and greater than 1 (Bins 5 and 6) are provided.