Introduction

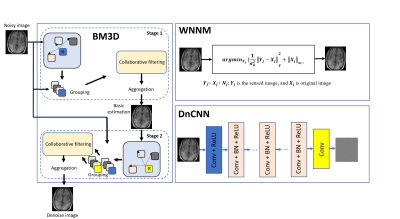
The challenge of fast MRI is to recover the original image from undersampled k-space data. SENSE¹ exploits the knowledge of sensitivity maps, and GRAPPA² uses the learned weighted-coefficients from ACS lines to estimate the missing k-space lines. Compressed sensing³ uses the idea that data can be compressed if undersampled artifacts are incoherent. Therefore, it introduces the concept of sparsity, achieved by regularization terms. L1-ESPIRiT⁴ also includes regularization terms in soft-SENSE reconstruction to iteratively find the optimal solution. After the PnP prior⁵ was first proposed by Venkatakrishnan et al, there have been several studies applying this concept to MRI ^6,7. Most of these studies focus on the CNN algorithm to complete the denoising process of the PnP algorithm. Alternatively, DnCNN⁸ may be a better fit. In this work, we explore three advanced denoiser algorithms to reconstruct four-fold undersampled MRI data using the PnP-ADMM framework. The idea behind BM3D⁹ is that given a local patch, it is not difficult to find many similar patches from nearby. These patches help with denoising, and this idea is typically true for medical images. The human brain, for example, has white matter, gray matter and cerebrospinal fluid, and thus has large nonlocal self-similarity in this sense. WNNM¹⁰ aims to improve conventional low rank algorithms by differently weighting singular values in nuclear norm, compared to the general solution which treats singular values equally in order to meet the convex property. Instead of directly outputting a denoised image, DnCNN learns a residual image, and this residual learning and batch normalization could benefit from each other, further improving the denoising performance. This neural network is more natural to combine with the PnP framework.

Methods

For MRI reconstruction, the collected signal can be written as: $$s(k_{x},k_{y})=\int_{}^{} \int_{}^{} \rho(x,y)e^{-i2\pi (k_{x}x+k_{y}y)}dxdy,$$
which can be written in matrix form as: $$y=Ax+n$$
where $$$y$$$ is the collected data and $$$x$$$ is the expected image; $$$A$$$ represents the sensor matrix; and $$$n$$$ is the noise. In MRI, reconstruction of undersampled data a with regularization term generally is written as follows: $$argmin_{x}||FSx-y||_2^2+\beta(x)$$
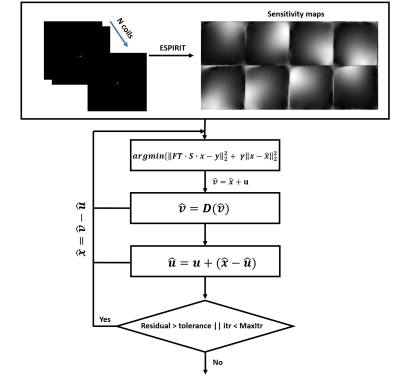
Here, $$$A$$$ is replaced by a sensitivity map weighted operator and a Fourier transform. The PnP-ADMM framework decouples data fidelity and the prior term by splitting variable $$$x$$$ into new variables $$$x$$$, $$$v$$$ and $$$u$$$, and its augmented Lagrangian for MRI reconstruction is $$L_{\gamma}(x,u,v)=||FSTx-y||_2^2+\beta s(v) + \gamma ||x+u-v||_2^2 - \gamma ||u||_2^2$$
Next, we repeat the following steps until convergence according to the ADMM algorithm¹¹, in which $$$\widehat{x}=\widehat{v}-u, \widehat{v}=\widehat{x}+u$$$.
$$\widehat{x}\leftarrow argmin_{x} ||FSx-y||_2^2 + \gamma ||x-\widehat{x}||_2^2 (1)$$
$$\widehat{v}\leftarrow argmin_{v} ||\widehat{v}-v||_2^2 + \gamma s(v) (2)$$
$$\widehat{u}\leftarrow u+(\widehat{x}-\widehat{v}) (3)$$
Here, (1) is a simple MAP estimate of $$$x$$$ with the given data $$$y$$$, and (2) is a denoising process. We could plug in advanced denoising algorithms. In this work, (2) was achieved with BM3D, WNNM and DnCNN.

The flowchart of PnP algorithm is illustrated in Figure 1, and a brief review of the three denoising algorithms is shown in Figure 2. Note that previous methods have used real and imaginary data as the input to the denoising algorithm. Here, we observed that using magnitude data and phase data leads to better performance for the PnP algorithm. BM3D, WNNM and DnCNN algorithms were download online^12-14. The tested data was from the NYU fastMRI dataset¹⁵, and the displayed brain data and ESPIRIT reconstruction are from Lustig’s ESPIRiT demo¹⁶. The undersampling pattern is generated with a variable-density Poisson distribution. Image quality was evaluated with two indexes: peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM), which are defined as follows: $$PSNR=10\cdot log_{10}\frac{max(X)^{2}}{MSE}$$
$$MSE=\frac{1}{mn}\sum_1^n\sum_1^m(X(i,j)-Y(i,j))^{2}$$
$$SSIM=\frac{(2\mu_{x}\mu_{y}+c_{1})(2\sigma_{xy}+c_{2})}{(\mu_x^2+\mu_y^2+c_{1})(\sigma_x^2+\sigma_y^2+c_{2})}$$
where $$$X$$$ is original image and $$$Y$$$ is noisy image with M-by-N matrix size. $$$\mu_{x}$$$and $$$\mu_{y}$$$ are means of images $$$X$$$ and $$$Y$$$ respectively. $$$\sigma_{x}$$$ and $$$\sigma_{y} $$$ are variances of $$$X$$$ and $$$Y$$$, and $$$\sigma_{xy}$$$ represents covariance of $$$X$$$ and $$$Y$$$. $$$c_{1}$$$ and $$$c_{2}$$$ are two variables to stabilize the division with a weak denominator.

Results

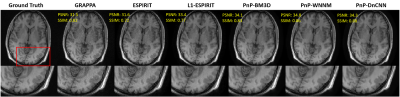
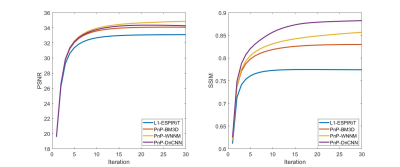
Figures 3 and 4 compare the PSNR and SSIM of the proposed three PnP-based methods and conventional methods with Cartesian data and an acceleration rate R = 4. Even though images reconstructed with GRAPPA suffer from noise, its SSIM is still high compared to ESPIRIT-based methods in which noise was indeed suppressed, but structure similarity decreased. Compared to conventional methods, both PSNR and SSIM of PnP-based methods have been improved: PnP-DnCNN preserved the best structure information while PnP-WNNM achieved highest PSNR.

Conclusion

MR reconstruction with advanced denoising algorithms under the PnP-ADMM framework is a flexible approach for image reconstruction. In this initial study, the approach outperformed conventional regularization methods in MRI at acceleration rate R = 4. Image reconstruction with higher acceleration rates in dynamic MRI and a comparison to PnP-CNN are underway.

Acknowledgements

We thank Prof. Charles Bouman for his wonderful youtube ECE 641 course. We learnt a lot PnP-related knowledge from his online course.