1159
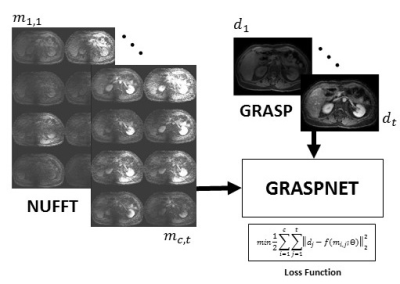
GRASPNET: Spatiotemporal deep learning reconstruction of golden-angle radial data for free-breathing dynamic contrast-enhanced MRI1Memorial Sloan Kettering Cancer Center, New York, NY, United States, 2GE Healthcare, New York, NY, United States
Synopsis
GRASP is a valuable tool to perform free-breathing dynamic contrast-enhanced (DCE) MRI with high spatial and temporal resolution. However, the 4D reconstruction algorithm is iterative and relatively long for clinical studies. In this work, we present a spatiotemporal deep learning approach to significantly reduce the reconstruction time without affecting image quality.
INTRODUCTION
GRASP combines golden-angle radial sampling and temporal compressed sensing to perform free-breathing dynamic contrast-enhanced (DCE) MRI with high spatial and temporal resolution [1]. 4D (3D+ time) image reconstruction is performed with an iterative algorithm, which results in long reconstruction times that limit clinical use. This work, proposes to replace the current GRASP iterative algorithm with a spatiotemporal deep learning approach named GRASPNET to reconstruct the dynamic images in a fraction of the time without degrading image quality. GRASPNET was trained and tested on DCE-MRI of patients with liver tumors.METHODS
Data acquisition: Free-breathing 3D abdominal imaging was performed on seventeen cancer patients with contrast injection on a 3T scanner (Signa Premier, GE Healthcare, Waukesha, WI). A product T1-weighted golden-angle stack-of-stars pulse sequence (DISCO STAR) was used with the following acquisition parameters: repetition time/echo time (TR/TE) = 4/1.9 ms, field of view (FOV) = 320×320×140 mm3 , number of readout points in each spoke = 480, flip angle= 12°, pixel bandwidth= 244 Hz and spatial resolution =1.6×1.6×5 mm3. A total of 1400 spokes were acquired, with a total scan time of approximately 3 minutes. GRASP: Peak of the contrast enhancement signal (corresponding to aorta peak) was found by averaging raw k-t data along coil and spoke dimensions and calculating maximum of the signal slope. 900 spokes were selected (300 spoke before the peak, 600 after). Twenty temporal frames (45 spokes in each frame) were generated by sorting the continuously acquired data and iterative GRASP reconstruction was performed to solve the following minimization problem [1]:$$d=argmin||FCd-m||_2+λ||Gd||_1$$
where F is non-uniform fast Fourier transform (NUFFT), C is the n-element coil sensitivity maps, m is the multicoil (c coils) radial data sorted into t temporal phases, d is the reconstructed time-resolved images, G is the temporal difference transform along the time dimension, and λ as regularization parameter that weights the sparsity term relative to data consistency.
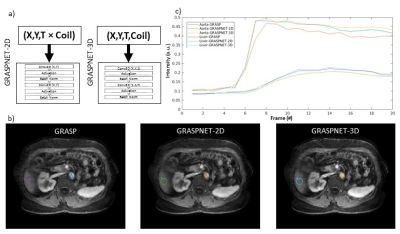
GRASPNET: A 3D convolutional neural network was designed with 10 layers. Each layer consists of two 3D convolution blocks, to explore spatial (kernel-size=2×2×1) and temporal (kernel-size=1×1×12) correlations explicitly [3]. Each convolution layer is followed by activation function (Sigmoid), batch normalization, and max pooling on the encoding path, and identical architecture was used on the decoding path except max pooling was replaced with deconvolution/upsampling [4]. This 3D network architecture (input=X,Y,T,Coil) was compared with a 2D version where coil and time dimensions were collapsed (input: (X,Y,T×Coil )) into a single dimension (Figure 2). The network was trained using GRASP reconstruction as a reference. To remove coil sensitivity profile, signal intensity was converted to relative enhancement followed by spatial filtering. Several runs were performed, where one subject was selected as a test set (array size = 256×256×52×20×8, where 8 represents the coil channels with 20 phases, and the remaining cases were (256×256×972×8) split into training (80%) and validation (20%). As shown in Figure 1, the input to the network is a multicoil undersampled dynamic image resulting from applying the NUFFT. 4D coil-combined dynamic images (output of GRASP) with 20 phases were used as reference to minimize the training loss function (the equation shown in Figure 1). ADAM optimizer with learning rate of 0.001 was used to find the mapping ( ) between then network input and output by updating the network weights (θ). Training was done on NVIDIA Tesla V100-SXM2-32GB with approximately 560 seconds training time in each epoch and a total number of 70 epochs.
RESULTS
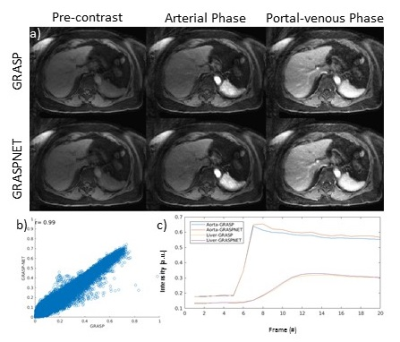
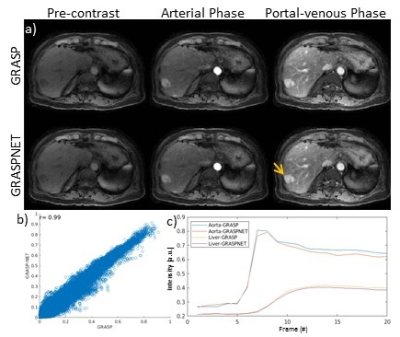
Reconstruction time for conventional iterative GRASP was approximately 180 minutes. Reconstruction time for the proposed GRASPNET was ~13 seconds, which represents an 800-fold reduction in reconstruction time. Figure 2 compares the performance of GRASPNET-2D and GRASPNET-3D network architectures. GRASPNET-3D outperforms GRASPNET-2D, due to the separation of spatial and temporal convolution filters which leads to a better exploitation of correlations along these different dimensions. Figure 3 compares the proposed GRASPNET with conventional GRASP in a patient demonstrating good qualitative and quantitative agreement (correlation coefficient=0.99), despite the 800-fold reduction in reconstruction time. ROI analysis along time shows similar contrast dynamics among the two in both liver and aorta. Figure 3 shows a similar comparison in a different patient case with liver lesion. Contrast, image details including the lesion (shown by yellow arrow) agree well between GRASPNET and conventional GRASP images with Correlation coefficient r=0.99.CONCLUSION
The proposed GRASPNET can achieve an 800-fold reduction in reconstruction time compared to the iterative GRASP algorithm with similar qualitative and quantitative performance. This work also presented a specific deep learning architecture to explicitly exploit spatial and temporal correlations, which was inspired by the original GRASP reconstruction that explicitly exploits transform sparsity along the time dimension.Acknowledgements
No acknowledgement found.References
1) Feng, L., Grimm, R., Block, K.T., Chandarana, H., Kim, S., Xu, J., Axel, L., Sodickson, D.K. and Otazo, R. (2014), Golden-angle radial sparse parallel MRI: Combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magn. Reson. Med., 72: 707-717. https://doi.org/10.1002/mrm.24980
2) Feng, L, Tyagi, N, Otazo, R. MRSIGMA: Magnetic Resonance SIGnature MAtching for real‐time volumetric imaging. Magn Reson Med. 2020; 84: 1280– 1292. https://doi.org/10.1002/mrm.28200
3) Küstner, T., Fuin, N., Hammernik, K. et al. CINENet: deep learning-based 3D cardiac CINE MRI reconstruction with multi-coil complex-valued 4D spatio-temporal convolutions. Sci Rep 10, 13710 (2020). https://doi.org/10.1038/s41598-020-70551-8
4) Jafari, R, Spincemaille, P, Zhang, J, et al. Deep neural network for water/fat separation: Supervised training, unsupervised training, and no training. Magn Reson Med. 2020; 00: 1– 15. https://doi.org/10.1002/mrm.28546
Figures