Introduction

For MR image denoising, various deep learning methods were proposed, showing promising results^1-5. However, these methods either require clean images, which are difficult to obtain, or redundancy from a specific MR sequence (e.g., multiple b-values in diffusion imaging⁴ or time-course in dynamic imaging⁵), limiting their applications. Recently, self-supervised learning methods such as noise to noise (N2N)⁶ showed promising performance. The method does not require a clean image but utilizes paired noise-corrupted images for training, improving requirements for training data. However, obtaining two noise-corrupted images in MR is still difficult, involving additional scans in most studies. In this study, we propose a new method, that does not require clean images nor acquisition of the paired noise-corrupted images. Our method generates a paired noise-corrupted images from single phased-array coil data and utilizes the pair for network training, requiring only raw multi-channel data. For inference, the method can input phased-array coil data or coil-combined image (e.g., DICOM images), enabling a wide application of the method. This new method is referred to as Coil to Coil (C2C) and is evaluated with synthetic data and applied to real data.

Methods

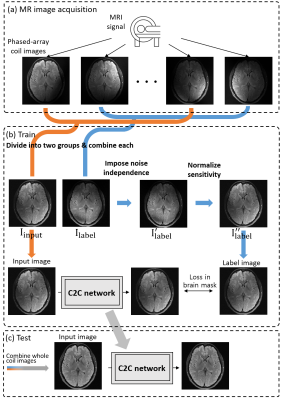
[Coil to Coil] In C2C, paired noise-corrupted images are generated from single phased-array coil data and then, the N2N algorithm⁶ is utilized to train a network. For N2N, the two noise-corrupted images need to satisfy three conditions: Firstly, two noise terms of the two images are independent. Secondly, the clean signals of the two images are the same. Lastly, the expectations of the noise terms are zero. C2C processes phased-array coil data to satisfy these conditions.

In MRI, ith coil image ($$$y_i$$$) can be formulated as $$$y_i=s_ix+n_i$$$ where $$$s_i$$$ is ith coil sensitivity and $$$n_i$$$ is noise $$$(i\in C=[1...c])$$$. To generate two noise-corrupted images, the coil images are randomly divided into two groups of equal numbers. Then, each group images are combined and labeled as $$$I_{input}$$$ and $$$I_{label}$$$ : $$$I_{input}=|\sum_js_j^Hy_j|$$$ and $$$I_{input}=|\sum_js_k^Hy_k|$$$ where $$$j\cup k=C$$$ and $$$j\cap k=0$$$. To impose independence in noise between the two combined images, generalized least-square was adopted voxel-wisely:$$\begin{bmatrix}I_{input}'\\I_{label}'\end{bmatrix}=\begin{bmatrix}1 & 0 \\\alpha & \beta \end{bmatrix}\begin{bmatrix}I_{input}\\I_{label}\end{bmatrix}$$ $$where, \alpha=\frac{-\sigma_{jk}}{\sqrt{\sigma_{jj}\sigma_{kk} - \sigma_{jk}^2}}, \beta=\frac{\sigma_{jj}}{\sqrt{\sigma_{jj}\sigma_{kk} - \sigma_{jk}^2}}$$ $$$\sigma_{jj}$$$, $$$\sigma_{kk}$$$, and $$$\sigma_{jk}$$$ were $$$\sum_j|s_j^H|^2var(N_j)$$$, $$$\sum_j|s_k^H|^2var(N_k)$$$, and $$$\sum_j|s_j^H||s_k^H|cov(N_j,N_k)$$$, respectively with $$$N_j$$$ and $$$N_k$$$ are noise in the input and label images, respectively. The noise variances and covariances were estimated using 400 pixels in the background and scaled by (2- $$$\pi$$$/2)^-1, correcting for the Rayleigh property. To normalize the sensitivity, the coil sensitivity of the two groups ($$$S_j=|\sum_js_j^H|$$$ and $$$S_k'=\alpha|\sum_ks_k^H| + \beta|\sum_js_j^H|$$$) are calculated in each voxel and the ratio ($$$S_j/S_k'$$$) was multiplied to $$$I_{label}'$$$ ($$$I_{label}''=(S_j/S_k')I_{label}'$$$). The condition of zero expectation noise is believed to be corrected for reasonably high SNR images. To avoid errors from the background which has Rayleigh distribution, the loss function was calculated with a brain mask. The loss function was defined as $$$E_{\in brainmask}|S_k'f_\theta(I_{input})-S_jI_{label}'|$$$. When testing the trained network (Fig. 1c), all coil images were combined and inferenced. Alternatively, we tested two grouped, each denoised, and combined results, revealing similar outcomes.

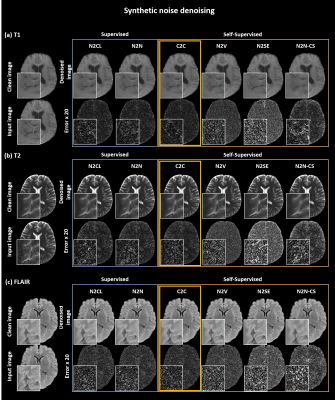
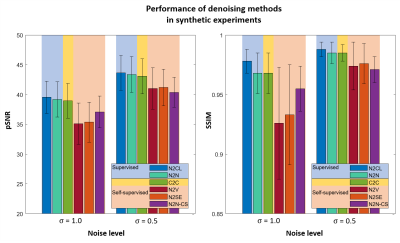
[Denoising of synthetic noise added images] Experiments were performed by adding synthetic noise to MRI images. FastMRI challenge dataset⁷ was utilized for training and test (34341 and 8284 slices, respectively; 3 contrasts). The sensitivity maps were estimated using ESPIRiT⁸. Two noise levels ($$$\sigma$$$) of 1.0 and 0.5 were tested. Noise correlation between any two coils was randomly chosen from 0 to 0.2. For the neural network, DnCNN⁹ and U-net¹⁰ were tested. To compare the performance of C2C, deep learning-based denoising methods (supervised: Noise to Clean (N2CL)¹¹, and N2N⁶; self-supervised methods: Noise to Void (N2V)¹², Noise to Self (N2SE)¹³, and a compressed sensing-based method (N2N-CS)⁶) were applied.

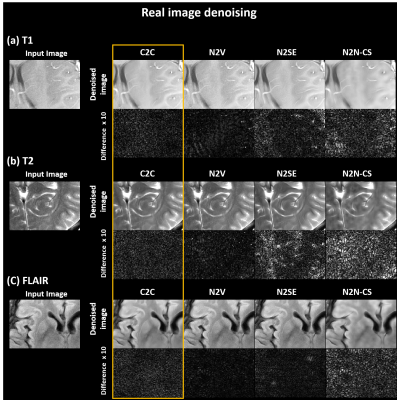
[Denosing of real images] Experiments were performed to denoise real images. A network for real noise denoising was trained and tested with the same data as before but with no additional noise. Since no clean images exist, C2C was compared only with self-supervised methods (N2V, N2Se, and N2N-CS).

Results

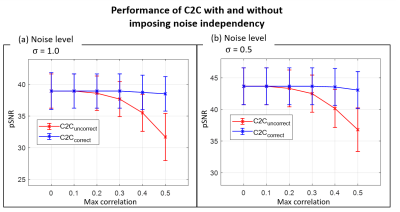
When tested, C2C successfully denoised the synthetic noise (Fig. 2) and real noise (Fig. 5; DnCNN results hereafter; U-net slightly underperforming). When applied to the synthetic noise added images, the C2C images show high-quality images that match to the original images with no or little structure-dependent errors in the difference images (all three contrasts). The quantitative metrics (Fig. 3) outperformed those of the other self-supervised methods, reporting comparable results to those of the supervised methods. When C2C was tested with and without noise independence processing (Fig. 4), the results show that the processing improves the robustness from noise correlation. In denoising real images (Fig. 5), C2C successfully improves all the images, revealing little or no structure-dependent signals in the noise maps.

Conclusion & Discussion

In this study, we proposed a self-supervised image denoising method, C2C, which generated paired noise-corrupted images from phased-array coil images to train a deep neural network. This method only requires multichannel data for network training and, therefore, can be easily utilized for other scans. C2C outperformed the other self-supervised methods and showed comparable results to the supervised methods. The method can be applied to DICOM images, enabling a wide use of the method.

Acknowledgements

This work has been supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government(MSIT)(No. 2021M3E5D2A01024795) and NRF-2021R1A2B5B03002783.