1140
Impact of diffusion tractography tracking parameters and smoothing polynomial order on muscle fiber measurements1Stephens Family Clinical Research Institute, Carle Health, Urbana, IL, United States, 2Carle Clinical Imaging Research Program, Carle Health, Urbana, IL, United States, 3Department of Radiology and Nuclear Medicine, Amsterdam Movement Sciences, Amsterdam University Medical Center, Amsterdam, Netherlands, 4Biomedical Engineering, Vanderbilt University, Nashville, TN, United States
Synopsis
Diffusion-tensor MRI tractography has been applied to characterize muscle diffusion properties and architecture. Tract propagation is performed using various propagation algorithms, settings, and step sizes. Smoothing, such as by polynomial fitting, has been shown to reduce tract path errors due to noise. Optimal settings for tracking algorithm, parameters, and order of subsequent smoothing polynomials have not been established. This work examines the effect of tracking algorithm settings, step size, and polynomial order on muscle architecture and diffusion estimates and polynomial fit residuals behavior. Results emphasize the high sensitivity of curvature estimates to smoothing polynomial order.
Introduction
Diffusion-tensor MRI tractography can provide information about properties relevant to muscle health and function, including architectural property estimates and diffusion properties such as mean diffusivity (MD) and fractional anisotropy (FA). Tract propagation has been performed using various tract propagation algorithms and parameters, including integration methods such as fiber assignment by continuous tracking (FACT)1,2, Euler2, and Runge Kutta2,3 with a range of propagation step sizes.4-7 Noise can introduce errors in the tract paths. Methods of path smoothing, such as by fitting a polynomial curve to the tract, have been used to reduce this impact of noise on tract architecture estimates.8 Optimal tracking algorithm/parameters and the most appropriate order for subsequent smoothing polynomials have not been established. This work examines the effect of tract propagation algorithm and settings, step size, and smoothing polynomial order on muscle architecture and diffusion estimates, and characterizes the smoothing polynomial fit residuals behavior.Methods
Seven healthy subjects consented to participate in this IRB-approved study. Axial diffusion and Dixon series of the leg were acquired at 3T with the knee extended and ankle 10° dorsiflexed. The diffusion images were registered to the Dixon images3, denoised9, and the diffusion-tensor series was calculated.3 Each subject’s tibialis anterior muscle and aponeurosis were segmented on the Dixon series in ITK-SNAP.10 The aponeurosis segmentation was converted to a mesh of seed points.Fiber-tracking was performed in MATLAB using publicly-available MuscleDTI_Toolbox.3 Euler and 4th-order Runge Kutta propagation algorithms were tested at four step sizes (0.25, 0.50, 0.75, 1.0 pixel-widths). Tracts were terminated at the muscle mask boundary, or earlier for FA <0.1 or >0.4, or if the trajectory angle between consecutive steps exceeded 30°. Two tract termination approaches were tested: propagation was stopped if FA or angle criterion was met at a single step (bin1) or two consecutive steps (bin2).
Each tract was smoothed by fitting independent polynomials, tested at 2nd, 3rd, 4th-order, to the x, y, and z coordinates. The residuals were analyzed for normality, autocorrelation, magnitude (sum of squares divided by number of points), and an F-test was performed to test for significant fit improvement (α=0.05) with higher polynomial order.
Tracts with length <10 mm, mean curvature >40 m-1, or pennation angle >40° were excluded. The length, curvature, pennation angle, mean diffusivity (MD), FA, and percentage of complete tracts (reached the muscle boundary) were calculated and averaged over all tracts and subjects.
Results
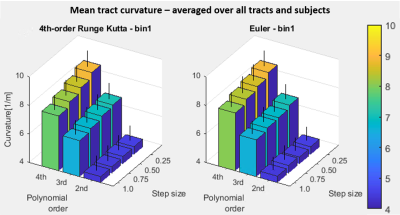
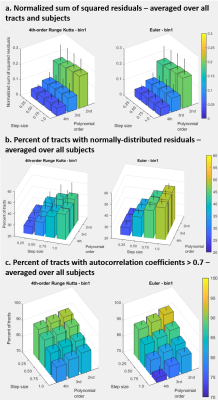
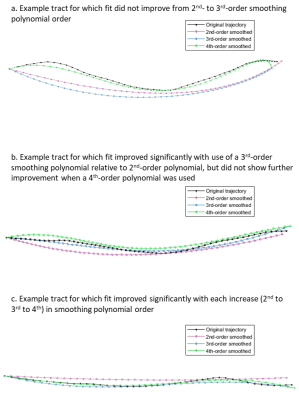
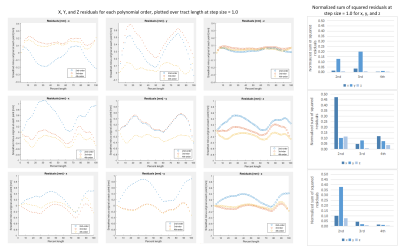
The mean estimated curvature was 4.4-4.6 m-1 over the range of settings with 2nd-order polynomial fitting, 6.5-7.0 m-1 (3rd-order), and 8.0-8.9 m-1 (4th-order) (Figure 1). Estimated curvature increased with decreasing step size but showed <1 m-1 difference between smallest and largest step sizes and did not vary between propagation algorithm or bin1/bin2 settings. Mean length was 63-64 mm, with the longest lengths at the largest step size/highest polynomial order combination, and for Runge Kutta compared to Euler. Pennation angle was 9° for all tests. MD and FA were consistently 1.8E-3 mm2/s and 0.22, respectively. The percent tracts complete was 93-94% for Runge Kutta and Euler bin1 tests and 94-95% for bin2.The normalized sum of squared residuals values were slightly higher with larger step size and approximately halved with each increase in polynomial order (0.18-0.21, to 0.08-0.10, to 0.05 mm2/step). The percent of tracts with normally distributed residuals was similar between polynomial orders but was higher at larger step sizes (25-27% at step=0.25 to 39-49% at step=1.0), with Euler resulting in the highest upper values. Percent tracts with autocorrelation coefficients >0.7 ranged from 73-82% at the highest polynomial order and step size to 88-92% at lowest order and step size (Figure 2). 62-69% of tracts showed significantly improved fit with 3rd-order polynomial fitting versus 2nd, and of these 55-59% showed further improvement with 4th-order fitting. Results were similar for x, y, and z coordinates. Figure 3 shows example tracts for no improvement with higher polynomial order (a), improvement from 2nd- to 3rd-order only (b), and improvement from 2nd- to 3rd- and 3rd- to 4th-order (c) and Figure 4 shows their associated residuals.
Discussion
The estimated length, pennation, MD, FA, and tract completeness did not vary appreciably with propagation algorithm, bin1/bin2 stopping methods, step size, and polynomial order. However, estimates of curvature were strongly influenced by polynomial order and moderately by step size, with results changing by 4.5 m-1 between 2nd-order/largest step size and 4th-order/smallest step size results. Higher polynomial order did result in better fit to the tract points, but comparison to ground-truth curvature measurements is needed to determine if higher-order polynomials provide a better fit to the actual fiber trajectories or lead to artificially increased curvature results. The analysis of residual behavior may provide a means for directing the selection of polynomial order when ground truth knowledge is not available.Conclusion
Most tractography results were insensitive to propagation algorithm and settings, and tract fit improved with increasing polynomial order. However, the sensitivity of curvature estimates, particularly to polynomial order, indicates that choice of fiber smoothing polynomial order or other smoothing approaches can lead to markedly different and potentially unrealistic curvature results. This highlights the need validating curvature estimates made under specific algorithm settings against a known ground-truth measurement.Acknowledgements
This work was supported by NIH/NIAMS grant R01 AR073831References
1. McMillan AB, Shi D, Pratt SJP, Lovering RM: Diffusion Tensor MRI to Assess Damage in Healthy and Dystrophic Skeletal Muscle after Lengthening Contractions. J Biomed Biotechnol 2011; 2011:1–10.
2. Weber M-A (Ed): Magnetic Resonance Imaging of the Skeletal Musculature. Berlin, Heidelberg: Springer Berlin Heidelberg; 2014. [Medical Radiology]
3. Damon BM, Ding Z, Hooijmans MT, et al.: A MATLAB toolbox for muscle diffusion-tensor MRI tractography. J Biomech 2021; 124:110540.
4. Charles JP, Suntaxi F, Anderst WJ: In vivo human lower limb muscle architecture dataset obtained using diffusion tensor imaging. PloS One 2019; 14:e0223531.
5. Froeling M, Nederveen AJ, Nicolay K, Strijkers GJ: DTI of human skeletal muscle: the effects of diffusion encoding parameters, signal-to-noise ratio and T 2 on tensor indices and fiber tracts: SIMULATIONS OF SKELETAL MUSCLE DTI. NMR Biomed 2013; 26:1339–1352.
6. Heemskerk AM, Sinha TK, Wilson KJ, Ding Z, Damon BM: Quantitative assessment of DTI-based muscle fiber tracking and optimal tracking parameters. Magn Reson Med 2009; 61:467–472.
7. Lansdown DA, Ding Z, Wadington M, Hornberger JL, Damon BM: Quantitative diffusion tensor MRI-based fiber tracking of human skeletal muscle. J Appl Physiol 2007; 103:673–681.
8. Damon BM, Heemskerk AM, Ding Z: Polynomial fitting of DT-MRI fiber tracts allows accurate estimation of muscle architectural parameters. Magn Reson Imaging 2012; 30:589–600.
9. Buck AKW, Ding Z, Elder CP, Towse TF, Damon BM: Anisotropic Smoothing Improves DT-MRI-Based Muscle Fiber Tractography. PLOS ONE 2015; 10:e0126953.
10. Yushkevich PA, Piven J, Hazlett HC, et al.: User-guided 3D active contour segmentation of anatomical structures: Significantly improved efficiency and reliability. NeuroImage 2006; 31:1116–1128.
Figures