1111
Model-Based Reconstruction with Automatic Differentiation for Single-Shot Myocardial T1 Mapping using Radial MOLLI with FLASH Readout1Institute for Diagnostic and Interventional Radiology, University Medical Center Göttingen, Göttingen, Germany, 2German Centre for Cardiovascular Research (DZHK), Partner Site Göttingen, Göttingen, Germany, 3Institute of Medical Engineering, Graz University of Technology, Graz, Austria
Synopsis
A nonlinear operator for radial MOLLI is constructed in BART, allowing accurate derivative calculation via automatic differentiation. The constructed nonlinear MOLLI operator is further integrated into a model-based reconstruction framework where myocardial $$$T_{1}$$$ maps are reconstructed directly from undersampled k-space data. Results on an experimental phantom and one healthy subject have demonstrated that high resolution ($$$1.0 \times 1.0 \times 6$$$ mm$$$^{3}$$$) myocardial $$$T_{1}$$$ maps can be achieved within 4 heartbeats with good accuracy and precision using the proposed method.
Introduction
Modified Look-Locker inversion recovery (MOLLI) [1] is one of the most widely used techniques for myocardial $$$T_{1}$$$ mapping and serves as a reference method due to its high precision and reproducibility [2]. However, MOLLI takes relatively long (11-17 heartbeats) and underestimates $$$T_{1}$$$ due to the imperfect signal model employed for fitting [3].Model-based reconstruction combined with non-Cartesian trajectories [4-8] constitutes one of the most efficient ways for quantitative MRI and has the potential to accelerate MOLLI. Here we adopt the radial FLASH readout for MOLLI [9-10]. To allow for accurate $$$T_{1}$$$ estimation, we constructed a nonlinear operator in BART [11] that models the signal evolution of MOLLI based on piece-wise analytical solutions of the Bloch equations. Thus, derivatives of the MOLLI signal with respect to the underlying physical parameters can be accurately calculated via automatic differentiation (AD) [12]. We further integrate the nonlinear operator into a previously developed model-based reconstruction framework [5,7], allowing further acceleration by directly estimating the physical parameters from undersampled k-space.
Methods
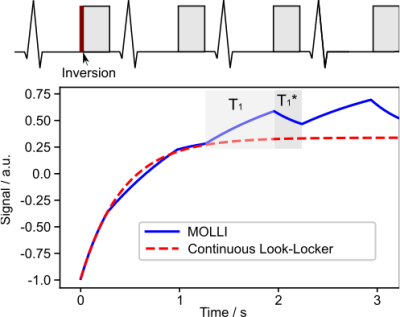
Radial MOLLI and Construction of the Nonlinear MOLLI OperatorThe radial MOLLI sequence is ECG-triggered and shown in Figure 1. Following a non-selective inversion, four trains of radial spokes were acquired at the end-diastolic phase at four consecutive cardiac cycles. Each cardiac cycle contains 80 spokes. As shown in Figure 1, the MOLLI signal alternates between $$$T_{1}^{*}$$$ relaxation (data acquisition) and $$$T_{1}$$$ relaxation (free recovery) during signal recovery, different from the mono-exponential recovery signal in the continuous Look-Locker acquisition.
To accurately model the signal evolution of MOLLI, we construct a nonlinear operator $$$M(\cdot)$$$ in BART by chaining nonlinear operators modeling the $$$T_{1}^{*}$$$ and $$$T_{1}$$$ processes. The output of each acquisition ($$$T_{1}^{*}$$$ model) is stacked along the time dimension such that the final operator (Figure 2) maps underlying physical parameter maps $$$(M_{0}, T_{1}, \alpha)^{T}$$$ to the $$$T_{1}$$$-weighted images ($$$Y$$$) at all inversion times. The nonlinear operator framework in BART allows computing the derivatives of $$$Y$$$ with respect to each parameter map via automatic differentiation.
Regularized Model-Based Reconstruction
The above nonlinear signal model is integrated into a previously developed model-based reconstruction framework [5], which formulates the estimation of physical parameters and coil sensitivity maps directly from k-space as a nonlinear inverse problem:$$ \hat{x}, \hat{C} = \text{argmin}_{x, C} \sum_{t_{k}}\sum_{i}\|P\mathcal{F}{C_{i}} \cdot {M_{t_{k}}(x)} - y_{i,t_{k}}\|_{2}^{2} + R({M_{0}, T_{1}}) + U(\alpha) + Q({C})$$where $$$M_{t_{k}}(x)$$$ is the constructed MOLLI model, evaluated at inversion time $$$t_{k}$$$ with the desired physical parameters $$$x = (M_{0}, T_{1}, \alpha)^{T}$$$. $$$C_{i}$$$ is the $$$i$$$-th coil sensitivity map, $$$P$$$ is the sampling pattern, $$$\mathcal{F}$$$ is the Fourier transform and $$$y_{i,t_{k}}$$$ is the acquired raw data. $$$R(\cdot)$$$ represents the joint $$$\ell_{1}$$$-Wavelet regularization, $$$U(\cdot)$$$ is the $$$\ell_{1}$$$-Wavelet regularization on $$$\alpha$$$ and $$$Q(\cdot)$$$ is the Sobolev regularization [13] enforcing coil smoothness. The above nonlinear inverse problem is then solved by the IRGNM-FISTA algorithm [5] in BART.
Experiments
All MRI studies were conducted on a 3T Skyra system (Siemens Healthineers, Erlangen, Germany) with approval of the local ethics committee. Combined thorax and spine coils with 26 channels were utilized for all scans. Phantom measurements were performed with simulated heartbeats from 40 to 100 bpm (4 heartbeats). All in-vivo scans were performed with 4 heartbeats and within a single breath-hold. The other acquisition parameters were: FOV $$$256\times256$$$ mm$$$^{2}$$$, in-plane resolution $$$1.0 \times 1.0$$$ mm$$$^{2}$$$, slice thickness 6 mm, TR/TE = 3.5/2.1 ms, FA = $$$6^{\circ}$$$, bandwidth 810 Hz/pixel and 320 radial spokes in total. For all reconstructions, 5 spokes were combined into one k-space frame, resulting in a temporal resolution of 17.5 ms.
Results
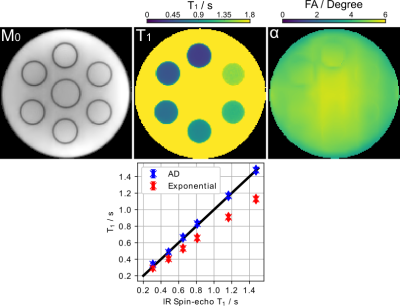
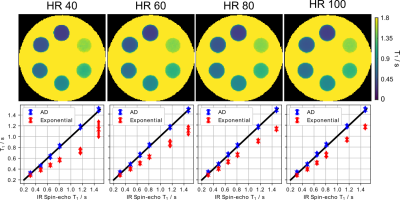
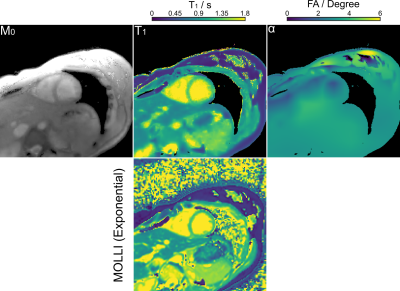
Figure 3 (top) shows the estimated physical parameter maps $$$(M_{0}, T_{1}, \alpha)^{T}$$$ for an experimental phantom with a simulated heart rate of 80 bpm. Visual inspection reveals good image quality achieved by the proposed method. Figure 3 (bottom) presents quantitative $$$T_{1}$$$ values for ROIs drawn into the 6 tubes. While the exponential model underestimates $$$T_{1}$$$, the proposed method achieves a good $$$T_{1}$$$ accuracy and precision in comparison to an IR spin-echo reference. Furthermore, Figure 4 confirms good $$$T_{1}$$$ accuracy and precision achieved by the proposed method at different heartbeats (40 - 100 bpm).Figure 5 (top) presents the reconstructed in-vivo physical maps $$$(M_{0}, T_{1}, \alpha)^{T}$$$. Again, visual inspection reveals good image quality. Despite the difference in breathing conditions, the proposed method produces comparable myocardial $$$T_{1}$$$ maps as the Cartesian 5(3)3 (11 heartbeats) MOLLI reference presented in Figure 5 (bottom). As expected, the myocardial septal $$$T_{1}$$$ value ($$$1330 \pm 50$$$ ms) of the proposed method is also higher than the reference ($$$1251 \pm 35$$$ ms), where the latter employs a mono-exponential model for fitting.
Discussion & Conclusion
In this work, we constructed a nonlinear operator for radial MOLLI in BART with calculation of the derivative via automatic differentiation. We further integrated the nonlinear MOLLI operator into a model-based reconstruction framework, estimating quantitative $$$T_{1}$$$ maps directly from k-space. Initial results on an experimental phantom and one healthy subject have demonstrated that high resolution ($$$1.0 \times 1.0 \times 6$$$ mm$$$^{3}$$$) myocardial $$$T_{1}$$$ maps can be achieved within four heartbeats with good accuracy and precision using the proposed method.Acknowledgements
Supported by the DZHK (German Centre for Cardiovascular Research).References
[1]. Messroghli DR, Radjenovic A, Kozerke S, Higgins DM, Sivananthan MU, Ridgway JP. Modified look-locker inversion recovery (MOLLI) for high-resolution T1 mapping of the heart. Magn Reson Med. 2004;52:141–6.
[2]. Moon JC, Messroghli DR, Kellman P, Piechnik SK, Robson MD, Ugander M, Gatehouse PD, Arai AE, Friedrich MG, Neubauer S, et al. Myocardial T1 mapping and extracellular volume quantification: a society for cardiovascular magnetic resonance (SCMR) and CMR working group of the european society of cardiology consensus statement. J Cardiovasc Magn Reson. 2013;15:92.
[3]. Kellman P, Hansen MS. T1-mapping in the heart: accuracy and precision. J Cardiovasc Magn Reson. 2014;16:2.
[4]. Block KT, Uecker M, Frahm J. Model-based iterative reconstruction for radial fast spin-Echo MRI. IEEE Trans Med Imaging. 2009;28:1759–69.
[5]. Wang X, Roeloffs V, Klosowski J, Tan Z, Voit D, Uecker M, Frahm J. Model-based T1 mapping with sparsity constraints using single-shot inversion-recovery radial FLASH. Magn Reson Med. 2018;79:730–40.
[6]. Becker KM, Schulz-Menger J, Schaeffter T, Kolbitsch C. Simultaneous high-resolution cardiac T1 mapping and cine imaging using model-based iterative image reconstruction. Magn Reson Med. 2019;81:1080–91.
[7]. Wang, X., Kohler, F., Unterberg-Buchwald, C. et al. Model-based myocardial T1 mapping with sparsity constraints using single-shot inversion-recovery radial FLASH cardiovascular magnetic resonance. J Cardiovasc Magn Reson. 2019;21:60.
[8]. Wang X, Tan Z, Scholand N, Roeloffs V, Uecker M. Physics-based reconstruction methods for magnetic resonance imaging. Phil Trans R Soc A. 2021;379:20200196.
[9]. Gensler D, Mörchel P, Fidler F, Ritter O, Quick HH, Ladd ME, Bauer WR, Ertl G, Jakob PM, Nordbeck P. Myocardial T1: quantification by using an ECG-triggered radial single-shot inversion-recovery MR imaging sequence. Radiology. 2014;274:879–87.
[10]. Marty B, Coppa B, Carlier P. Fast, precise, and accurate myocardial T1 mapping using a radial MOLLI sequence with FLASH readout. Magn Reson Med. 2018;79:1387–98.
[11]. Uecker et al., "BART Toolbox for Computational Magnetic Resonance Imaging", Zenodo, DOI: 10.5281/zenodo.592960.
[12]. Baydin AG, Pearlmutter BA, Radul AA, Siskind AA. Automatic differentiation in machine learning: A survey. J Mach Learn Res. 2017;18(1):5595–5637.
[13]. Uecker M, Hohage T, Block KT, Frahm J. Image reconstruction by regularized nonlinear inversion – joint estimation of coil sensitivities and image content. Magn Reson Med 2008; 60: 674– 682.
Figures