1100
Optimal Singular-Value Shrinkage for fMRI Denoising
Mo Shahdloo1 and Mark Chiew1
1Wellcome Centre for Integrative Neuroimaging (WIN), FMRIB, University of Oxford, Oxford, United Kingdom
1Wellcome Centre for Integrative Neuroimaging (WIN), FMRIB, University of Oxford, Oxford, United Kingdom
Synopsis
Singular-value truncation techniques have shown promise for reducing thermal noise in fMRI, where singular-values below a certain threshold are assumed to be noise and are discarded. However, this approach could lead to suboptimal signal recovery, since the remaining singular-values could still have variance contributed by noise. Here instead we propose to use a theoretically MSE-optimal function to shrink the remaining singular-values. The proposed method is evaluated using simulations and high-resolution in-vivo human brain data, and is shown to improve signal-to-noise ratio and functional statistics while leaving the spatial precision intact.
Introduction
Thermal noise —that under linear image reconstruction is assumed to be zero-mean complex Gaussian distributed— can dominate the fMRI signal at high imaging resolutions (e.g., in laminar fMRI)1. This motivates the development of denoising methods to extract the relevant signals from noisy, complete measurements. A recently proposed promising method, NORDIC2, works by singular-value hard-thresholding (SVHT) of spatiotemporal matrices formed by image patches. Presuming that small singular-values should only be contributed to by noise, NORDIC truncates singular-values below an empirical threshold found using a Monte-Carlo simulation.However, any choice of a hard threshold would lead to suboptimal denoising because the remaining components could still be biased by noise. Effectively, SVHT would result in the best low-rank estimate of the noisy matrix, while leaving the problem of estimating the true underlying data matrix unanswered. This issue is even more pronounced in an ultra low-SNR regime where thermal noise could also inflate a considerable number of retained singular-values.
Instead we propose to apply a function to shrink the remaining singular-values. In the context of random matrix theory, recently a shrinkage function has been proposed that can guarantee optimality in the MSE sense4. Here, we used preprocessing steps similar to NORDIC to make the thermal noise identically distributed, but then unlike NORDIC, we used this shrinkage function to deflate the singular-values in each spatiotemporal patch. The proposed method is evaluated using simulations and high-resolution 7T human fMRI data where it shows improved performance compared to NORDIC, without introducing extra spatial smoothing penalties.
Methods
We consider the reconstructed complex-valued volumetric fMRI image series $$$m\in\mathbb{C}^{N_xN_yN_zN_t}$$$ where $$$N_x,N_y,N_z$$$ are spatial dimensions, and $$$N_t$$$ is the number of time frames. For each voxel a $$$p_xp_yp_z$$$ image patch at each time frame $$$\tau={1...N_t}$$$ is vectorised to $$$y_\tau$$$. These vectors are then used to generate a noisy data matrix $$$\mathbf{Y}\in\mathbb{C}^{MN_t}$$$, where $$$M=p_xp_yp_z$$$.Normalising the data by the g-factor maps estimated separately makes the thermal noise independent identically distributed (iid) across the field of view3. Then, assuming the noise matrix $$$\mathbf{Z}$$$ to have entries with zero mean and unit variance, the denoising problem is to recover the underlying data matrix $$$\mathbf{X}$$$ by minimising the mean-squared error $$$||\mathbf{X}-\mathbf{\hat{𝐗}}||_F^2$$$, where $$$\mathbf{\hat{𝐗}}$$$ is the estimated data, under the model $$$\mathbf{𝐘}=\mathbf{𝐗}+\mathbf{Z}$$$.
Take $$$\mathbf{𝐘}=\sum_{i=1}^my_iv_iu_i$$$ for the Singular-Value Decomposition of $$$\mathbf{𝐘}$$$, where $$$v_i$$$ and $$$u_i$$$ are the right and left singular vectors corresponding to the singular-value $$$y_i$$$. We wish to use a shrinkage function $$$\eta(y)$$$ such that the estimate $$$\mathbf{\hat{𝐗}}=\sum_{i=1}^m\eta(y_i)v_iu_i$$$ is MSE-optimal. It has been shown that such a function is well defined and can be expressed as4$$\eta(y)=\begin{cases}\frac{1}{y}\sqrt{(y^2-\beta-1)^2-4\beta}&y\ge1+\sqrt{\beta}\\0&y<1+\sqrt{\beta}\end{cases}$$where $$$\beta=M/N_t$$$ (Fig. 1). For the general case of noise level $$$\sigma$$$, calibrated shrinker $$$\eta_\sigma(y)=\sigma\eta(y/\sigma)$$$ should be used4.
In a simulation experiment, 120 frames of a 217x181x10 dimensional noise-free simulated phantom data were corrupted by iid Gaussian noise with zero mean and standard deviation $$$\sigma\in\{0.08...0.16\}$$$ relative to signal strength. A patch size of 5x5x5 was used. MSE was compared between NORDIC and the proposed approach.
Furthermore, in-vivo fMRI data from a block-design (30secs on/off) experiment with flickering checkerboard visual stimuli were acquired on a 7T scanner with parameters: 3D GE-EPI, 32channel head coil, 0.67mm isotropic voxels, 28 slices, 128 volumes, R=4 iPAT, TR/TE=2400/30, FA=20°, 288x214 matrix size. Data in each channel were denoised individually and then combined, and the GLM models were fit. We evaluated the proposed method against NORDIC by comparing temporal signal-to-noise ratio (tSNR), model goodness of fit, z-statistics, and smoothness of the residual field.
Results
Figure 2 shows the simulation results. The proposed method performs better than NORDIC denoising in reducing the MSE, at all tested noise levels.Figure 3 shows the tSNR improvement in the in-vivo dataset. This tSNR gain is reflected in reduced model fit residuals, as shown in Figure 4, demonstrating more accurate GLM fits compared to NORDIC.
Figure 5 shows the thresholded z-score activation maps, and their distribution. The proposed method yields significant gain in the voxelwise z-scores (bootstrap test,$$$p<10^{-4}$$$), leading to more voxels with significant activation.
Moreover, to ensure that the proposed denoising method does not lead to oversmoothing, the full-width at half maximum (FWHM) of the residual field5 were compared as a proxy indicating the image smoothness. FWHM across read-out, phase-encoding, and slice direction is [1.38,1.29,1.22]mm in the proposed method, and is [1.36,1.27,1.22]mm using NORDIC, demonstrating that the proposed method does not achieve improved denoising performance at the cost of overly spatial smoothing.
Conclusion
Singular-value hard thresholding for patch-based fMRI denoising is suboptimal. We propose a denoising method based on optimal shrinkage of individual singular-values that minimises the MSE. The proposed approach is evaluated using simulations and high-resolution in-vivo fMRI experiments, and is shown to enhance functional data quality more than what is achievable with similar SVHT-based methods. However, a limitation of this method is that similar to other SVHT-based denoising methods, shrinking any number of singular-values to zero could reduce temporal degrees of freedom, potentially skewing the statistical analyses downstream. In conclusion, the proposed approach provides a simple analytical function to modify the singular-values, eliminating the need for ad-hoc thresholds. It can make fMRI more efficient, enabling faster acquisitions without the need to radically change the current denoising pipelines.Acknowledgements
M.C. is supported by the Royal Academy of Engineering (RF201617/16/23). The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z).References
- Huber L, Handwerker DA, Jangraw DC, Chen G, Hall A, Stüber C, Gonzalez-Castillo J, Ivanov D, Marrett S, Guidi M, Goense J. High-resolution CBV-fMRI allows mapping of laminar activity and connectivity of cortical input and output in human M1. Neuron. 2017 Dec 20;96(6):1253-63.
- Vizioli L, Moeller S, Dowdle L, Akçakaya M, De Martino F, Yacoub E, Uğurbil K. Lowering the thermal noise barrier in functional brain mapping with magnetic resonance imaging. Nature communications. 2021 Aug 30;12(1):1-5.
- Moeller S, Pisharady PK, Ramanna S, Lenglet C, Wu X, Dowdle L, Yacoub E, Uğurbil K, Akçakaya M. NOise Reduction with DIstribution Corrected (NORDIC) PCA in dMRI with complex-valued parameter-free locally low-rank processing. NeuroImage. 2021 Feb 1;226:117539.
- Gavish M, Donoho DL. Optimal shrinkage of singular values. IEEE Transactions on Information Theory. 2017 Jan 17;63(4):2137-52.
- Jenkinson M. Estimation of smoothness from the residual field. Internal Technical Report TR00MJ3 2000. Oxford, UK: University of Oxford.
Figures
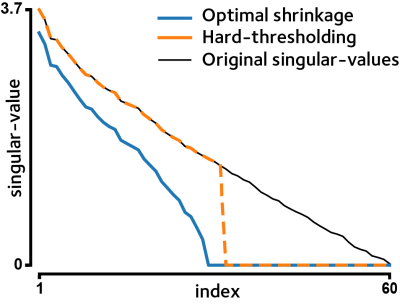
Figure 1. A single slice of the simulated brain phantom data were corrupted by iid standard Gaussian noise. Singular-values of the noisy data is shown. Hard-thresholding discards all singular values below a certain threshold, but the surviving singular-values could also be inflated by noise. Optimal shrinkage reduces the contribution of noise in the remaining singular-values, yielding a MSE-optimal estimate of the ground-truth data.
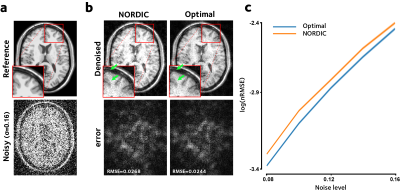
Figure 2. Denoising of the simulated brain phantom. (a) The reference data were corrupted by standard Gaussian noise, and (b) were denoised using NORDIC and using the proposed method. Optimal shrinkage of singular-values leads to reduced MSE, (c) consistently across all tested noise levels (mean±std across slices and time).
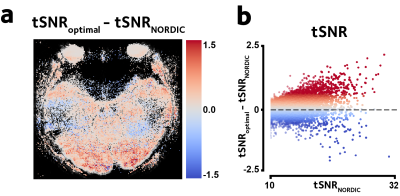
Figure 3. Improvement in voxelwise tSNR in a representative slice from the in-vivo dataset is shown. (a) The proposed method yields higher tSNR compared to the SVHT-based method NORDIC. (b) tSNR enhancement is more pronounced in voxels where signal contribution is higher.
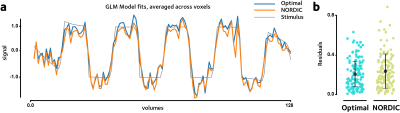
Figure 4. (a) tSNR enhancement leads to more accurate GLM fits, (b) reflected in reduced GLM model fitting residuals.
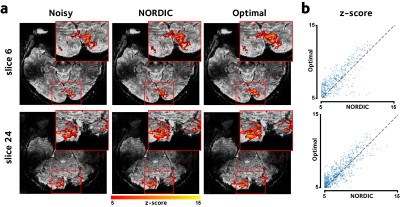
Figure 5. Voxelwise z-scores of the fit GLM models are shown in two representative slices. (a) The proposed method leads to a higher number of voxels with activations above the threshold. (b) Moreover, the z-scores in the shown voxels are higher using the proposed method compared to NORDIC.
DOI: https://doi.org/10.58530/2022/1100