1099

Field-Mapping-Embedded EPI for Geometric Distortion Correction

Didi Chi¹, Yasmin Blunck^1,2, Rebecca Glarin², Catherine E. Davey^1,2, Daniel Staeb³, and Leigh A. Johnston^1,2
¹Department of Biomedical Engineering, University of Melbourne, Parkville, Australia, ²Melbourne Brain Centre Imaging Unit, University of Melbourne, Parkville, Australia, ³MR Research Collaborations, Siemens Healthcare Pty Ltd, Melbourne, Australia

Synopsis

A Field-Mapping-Embedded (FME) EPI sequence is proposed in which the map is acquired during EPI acquisition without increasing scan time, using phase-encoded phase correction navigators. Results from in vivo experiment demonstrate accurate measurement and robust geometric distortion that performs favourably in comparison with existing techniques that require additional scans.

Introduction

Echo planar imaging is well-known to be sensitive to field inhomogeneities ($$$\Delta{B_0}$$$) due to its prolonged readout time, leading to geometric distortion in the resultant images¹. Methods to correct geometric distortion in EPI images can be classified into two primary categories based on the estimated $$$\Delta{B_0}$$$ mapping procedure^2,3, using either a) two EPI images with reversed phase-encoding directions⁴ or b) a double gradient-echo sequence¹. Both classes of methods require the acquisition of a sequence additional to EPI, increasing both scan time and potential realignment errors.
The current study proposes a Field-Mapping-Embedded (FME) EPI sequence, which enables measurement of $$$\Delta{B_0}$$$ map concurrently with the EPI acquisition. The FME-EPI technique exploits existing phase correction (PC) lines for N/2 ghosting correction⁵. As multiple measurements are taken in an fMRI study, we leverage the redundancy in the navigators repeated in each measurement by way of additional phase encoding so that full k-space information is acquired for $$$\Delta{B_0}$$$ mapping over EPI readouts. Unlike other simultaneous field-mapping EPI sequences^6,7,8, FME-EPI does change the EPI trajectory and hence has no deleterious effect on sequence timing. An efficient distortion correction procedure using the FME-EPI-estimated $$$\Delta{B_0}$$$ map completes the proposed technique.

Theory

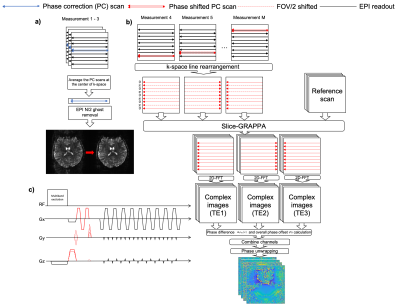
Field-Mapping-Embedded EPI sequence design
The FME-EPI sequence uses conventional PC scans (3 non-phase encoded echoes at the beginning of each EPI readout train) to correct for N/2 ghosting across each N-volume time-series (Figure 1a). For the remaining image volumes, variable phase encoding gradients are added before and after the PC lines in each slice (Figure 1b,c). To facilitate the multi-band acquisition, the slice rephasing gradient is alternated every second measurement to introduce a FOV/2 CAIPIRINHA^9,10 shift (Figure 1b,c).

$$$\Delta{B_0}$$$ estimation and distortion correction
After reordering the phase-encoded PC scans (Figure 1b), complex images at three echo times ($$$I_{{TE}_1}$$$, $$$I_{{TE}_2}$$$, $$$I_{{TE}_3}$$$) are reconstructed by slice-GRAPPA¹⁰ using a FLASH-based reference scan¹¹. Local field variation $$$\Delta\varphi_{31}$$$ and overall phase offset $$$\varphi_0$$$ are derived based on these three images.
$$$I_{{TE}_1}$$$ and $$$I_{{TE}_3}$$$ are used for calculating $$$\Delta\varphi_{31}$$$,
$$\Delta\varphi_{31} = \angle{\sum_{ch}I_{{TE}_3} \cdot I^{*}_{{TE}_1}}$$ The three complex images are used to find $$$\varphi_0$$$: $$\Delta\varphi_{2,1}(x,y,\Delta TE) = \gamma \Delta B_0(x,y)\Delta TE + ax + b^{\prime}_1 = \angle{\sum_{ch}I_{{TE}_2} \cdot I^{*}_{{TE}_1}}$$ $$\Delta\varphi_{3,2}(x,y,\Delta TE) = \gamma \Delta B_0(x,y)\Delta TE - ax - b^{\prime}_2 = \angle{\sum_{ch}I_{{TE}_3} \cdot I^{*}_{{TE}_2}}$$
The linear phase shift $$$ax$$$ and constant phase offset $$$b^{\prime}_1$$$, $$$b^{\prime}_2$$$ are estimated by linear fit of the phase data ($$$\Delta \varphi_{21}$$$, $$$\Delta \varphi_{32}$$$) along the readout direction¹². After removing the linear phase shift, $$$ax$$$, $$\Delta \varphi_{21}(x,y,\Delta TE)=\gamma\Delta{B_0}(x,y)\Delta{TE}+b^{\prime}_1$$ $$\Delta\varphi_{32}(x,y,\Delta TE)=\gamma\Delta{B_0}(x,y)\Delta{TE}-b^{\prime}_2$$ $$$\Delta\varphi_{31}=\Delta\varphi_{21} + \Delta\varphi_{32}=2\gamma\Delta{B_0}(x,y)\Delta{TE}+b^{\prime}_1-b^{\prime}_2\Rightarrow\varphi_0=b^{\prime}_1-b^{\prime}_2$$$.
Fast phase-unwrapping is achieved using Herráez et al’s method¹³.
Phase-unwrapped local field variation ($$$\Delta\varphi_{31,\text{unwrapped}}$$$) and overall phase offset ($$$\varphi_0$$$) are considered in $$$\Delta{B_0}$$$ map calculation: $$\Delta{B_0}(x,y)=\frac{\Delta\varphi_{31,\text{unwrapped}} - \varphi_0}{2\gamma\Delta{TE}}$$
Voxel displacement shift maps (VDM) are calculated by $$\text{VDM}(x,y) = \gamma\Delta{B_0}(x,y)\cdot \Delta{TE}_{\text{eff}}, \Delta{TE}_{\text{eff}}=\frac{\Delta{TE}}{R}$$ where $$$N$$$ is the matrix size and $$$R$$$ is the in-plane acceleration factor.
Distortion correction is implemented by resampling the distorted image along the phase-encoding direction by linear interpolation based on VDM: $$I(x,y^\prime) = I(x,y + \text{VDM}(x,y))$$

Method

Data acquisition
A healthy volunteer (female, aged 26, written consent obtained) was scanned on an investigational 7T whole-body MRI scanner (Magnetom 7T plus, Siemens Healthcare, Erlangen, Germany) using an 8Tx-32Rx head-coil (Nova Medical Inc. USA). Multiband FME-EPI was acquired: TE/TR=33/1700ms, resolution=1.8mm-isotropic, phase-encoding direction=AP, R=2, MB-factor=4, 84 slices, $$$\Delta{TE}$$$=0.6ms, 119 measurements). Two conventional EPI time-series with the same timing parameters and both phase-encoding directions were also acquired. A double gradient-echo sequence (TE1/TE2=3.3/4.4ms, resolution=4mm-isotropic, number of slices=40) was acquired for $$$\Delta{B_0}$$$ comparison purposes. MP2RAGE T1-w images were acquired for anatomical reference (TI1/TI2=700/2700ms, TE/TR=1.93/4500ms, resolution=1mm-isotropic).

Comparisons
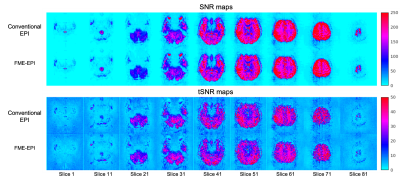
Time-course SNR ($$$\frac{\mu}{\sigma_t}$$$) and image SNR were calculated for conventional EPI and FME-EPI data. Brain extraction was performed using BET¹⁴ before calculating the mean SNR and tSNR. EPI N/2 ghosting was corrected in the same way as for conventional EPI processing⁵. Standard deviation of the bottom 20 lines in the images was calculated ($$$\sigma_{\text{ghost}}$$$) to evaluate N/2 ghost correction. FME-EPI distortion correction was compared to FUGUE^1,15 and TOPUP⁴.

Results & Discussion

The ghost-removal metric ($$$\sigma_{\text{ghost,EPI}}$$$: 40.69, $$$\sigma_{\text{ghost,FME-EPI}}$$$: 40.92) and resultant images (Figure 2) demonstrate the utility of the first three PC scans for N/2 ghosting removal, with comparable SNR and tSNR. Note that the three PC scans may be repeated and located arbitrarily in an fMRI time-series to minimize the effect of motion on N/2 ghost removal.
$$$\Delta{B_0}$$$ maps calculated using FME-EPI compare favourably with the double echo sequence (Figure 3) and are of the same FOV and resolution as the EPI readout, thus requiring no realignment or resampling to match the image data.
The FME-EPI distortion correction is more accurate than FUGUE, particularly in the frontal lobe (Figure 4, 1st-2nd row). Compared to TOPUP, FME-EPI distortion correction does not contain the artifacts evident around the ventricles from which TOPUP commonly suffers (Figure 4, 3rd-4th row).

Conclusion

The proposed FME-EPI method acquires the $$$\Delta{B_0}$$$ map concurrently with EPI readout, maximizing scan time efficiency. Results from in vivo experiments have demonstrated $$$\Delta{B_0}$$$ map estimation and distortion correction that outperforms existing techniques. Future works involve optimization of number of phase-encoded PC lines required, thus minimizing sensitivity to motion and the application of FME-EPI in fMRI studies beyond the current proof-of-concept.

Acknowledgements

We acknowledge the facilities, and the scientific and technical assistance of the Australian National Imaging Facility, a National Collaborative Research Infrastructure Strategy (NCRIS) capability, at the Melbourne Brain Centre Imaging Unit of the University of Melbourne. The work is also supported by a research collaboration agreement with Siemens Healthineers.

References

1. Jezzard, P., & Balaban, R. S. Correction for geometric distortion in echo planar images from B0 field variations. Magnetic Resonance in Medicine. 1995; 34(1): 65-73.

2. Abreu, R., & Duarte, J. V. Quantitative Assessment of the Impact of Geometric Distortions and Their Correction on fMRI Data Analyses. Frontiers in Neuroscience. 2021; 15: 211.

3. Schallmo, M. P., Weldon, K. B., Burton, P. C., et al. Assessing methods for geometric distortion compensation in 7 T gradient echo functional MRI data. Human Brain Mapping. 2021; 42(13): 4205-4223.

4. Andersson, J. L., Skare, S., & Ashburner, J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage. 2003; 20(2): 870-888.

5. Heid, O. Method for phase correction of nuclear magnetic resonance signals. Magnetic Resonance Imaging. 1997; 15(4): XXIII

6. Roopchansingh, V., Cox, R. W., Jesmanowicz, A., et al. Single‐shot magnetic field mapping embedded in echo‐planar time‐course imaging. Magnetic Resonance in Medicine. 2003: 50(4), 839-843.

7. Priest, A. N., De Vita, E., Thomas, D. L., et al. EPI distortion correction from a simultaneously acquired distortion map using TRAIL. Journal of Magnetic Resonance Imaging. 2006; 23(4): 597-603.

8. Techavipoo, U., Lackey, J., Shi, J., et al. Phase labeling using sensitivity encoding (PLUS): Data acquisition and image reconstruction for geometric distortion correction in EPI. Magnetic Resonance in Medicine. 2009; 61(3), 650-658.

9. Breuer, F. A., Blaimer, M., Heidemann, R. M., et al. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi‐slice imaging. Magnetic Resonance in Medicine. 2005 53(3): 684-691.

10. Setsompop, K., Gagoski, B. A., Polimeni, J. R., et al. Blipped‐controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g‐factor penalty. Magnetic Resonance in Medicine. 2012; 67(5): 1210-1224.

11. Talagala, S. L., Sarlls, J. E., Liu, S., et al. Improvement of temporal signal‐to‐noise ratio of GRAPPA accelerated echo planar imaging using a FLASH based calibration scan. Magnetic Resonance in Medicine. 2016; 75(6): 2362-2371.

12. Feng, W., Neelavalli, J., & Haacke, E. M. Catalytic multiecho phase unwrapping scheme (CAMPUS) in multiecho gradient echo imaging: removing phase wraps on a voxel‐by‐voxel basis. Magnetic Resonance in Medicine. 2013; 70(1): 117-126.

13. Herráez, M. A., Burton, D. R., Lalor, M. J., et al. Fast two-dimensional phase-unwrapping algorithm based on sorting by reliability following a noncontinuous path. Applied optics. 2002; 41(35): 7437-7444.

14. Smith, S.M. Fast robust automated brain extraction. Human Brain Mapping. 2002; 17(3): 143-155

15. Jenkinson, M. Improving the registration of B0-disorted EPI images using calculated cost function weights. Tenth Int. Conf. on Functional Mapping of the Human Brain. 2004

Figures

Figure 1: FME-EPI sequence: a) For the first three measurements, PC lines are acquired at the center of k-space similar to conventional EPI; b) From fourth volume onwards, PC lines are phase-encoded to enable on-the-fly $$$\Delta{B_0}$$$ mapping; c) FME-EPI sequence diagram with red lines representing the phase-shifted PC scans and corresponding slice rephasing gradients, black lines representing EPI readouts.

Figure 2 1st row: SNR maps of a conventional EPI time-series (mean ($$$\pm\sigma$$$) after brain extraction $$$186.39\pm109.69$$$). 2nd row: SNR maps of the FME-EPI time-series (mean ($$$\pm\sigma$$$) after brain extraction $$$181.27\pm103.39$$$). 3rd row: tSNR maps of a conventional EPI (mean ($$$\pm\sigma$$$) after brain extraction $$$25.94\pm14.25$$$).4th row: tSNR maps of the FME-EPI time series (mean ($$$\pm\sigma$$$) after brain extraction $$$25.29\pm13.56$$$).

Figure 3 $$$\Delta B_0$$$ maps obtained by a) FME-EPI and b) the double-echo sequence.

Figure 4 comparison of different distortion correction methods: Column 1) Distorted EPI images, 2) TOPUP, 3) FUGUE, 4) the proposed FME-EPI method.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

1099

DOI: https://doi.org/10.58530/2022/1099