1098
Non-Local Means Denoising of 7T Functional MR Images: Enhancing Spatial Accuracy of Fine-Grained Task-Specific Neurosignatures?
Igor Fabian Tellez Ceja1, Thomas Gladytz1, Ludger Benedikt Starke1, Karsten Tabelow2, Thoralf Niendorf1,3, and Henning Matthias Reimann1
1Berlin Ultrahigh Field Facility (B.U.F.F.), Max Delbrück Center for Molecular Medicine, Berlin, Germany, 2Weierstrass Institute for Applied Analysis and Stochastics, Berlin, Germany, 3Experimental and Clinical Research Center (ECRC), a joint cooperation between the Charité Medical Faculty and the Max Delbrück Center for Molecular Medicine in the Helmholtz Association, Berlin, Germany
1Berlin Ultrahigh Field Facility (B.U.F.F.), Max Delbrück Center for Molecular Medicine, Berlin, Germany, 2Weierstrass Institute for Applied Analysis and Stochastics, Berlin, Germany, 3Experimental and Clinical Research Center (ECRC), a joint cooperation between the Charité Medical Faculty and the Max Delbrück Center for Molecular Medicine in the Helmholtz Association, Berlin, Germany
Synopsis
Superior spatial fidelity of fMRI at ultrahigh magnetic field strengths (≥7T) in principle allows for resolving fine grained task-specific fMRI neurosignatures. Yet, spatial details of BOLD clusters are conventionally blurred by Gaussian smoothing. To preserve spatial details, spatial-adaptive non-local means (SANLM) denoising has been introduced in fMRI as an alternative to Gaussian smoothing. Here, we evaluate SANLM denoising at 7T. SANLM removes noise in homogeneous areas while maintaining edges. It prevents the spread of BOLD patterns between adjacent brain regions, but should be employed with caution, as its spatial detail is partially driven by the underlying anatomy.
Introduction
The high spatial resolution at ultrahigh magnetic field strengths (UHF, ≥7T) in principle allows for resolving fine grained task-specific fMRI neurosignatures within brain areas, e.g. at the level of cortical layers or small subcortical nuclei. Yet, Gaussian smoothing, which is conventionally applied in univariate fMRI analysis, causes a substantial loss of spatial accuracy by blurring the anatomical boundaries and introducing confounding effects from neighboring voxels. To preserve spatial accuracy, we explored spatial-adaptive non-local means (SANLM) denoising1 at UHF, which has been recently introduced as a superior alternative to Gaussian smoothing for fMRI2. We evaluated the performance of three different SANLM filter strengths in respect with the two key features of spatial smoothing: (1) improving signal-to-noise ratio (SNR), and (2) ensuring a sufficient smoothness of the data to meet the criteria of random field theory (RFT) for inference at cluster-level to further increase sensitivity to blood oxygen level-dependent (BOLD) effects. Preserving spatial accuracy of BOLD patterns with high SNR, under the criteria of RFT, would allow for detailing fine-grained task-specific patterns within small anatomical areas, which would constitute a major leap forward en route to identifying pain-specific functional neurosignatures across the brain via fMRI at UHF.Methods
A BOLD fMRI experiment was carried out on one healthy participant, employing eight brief (100 ms) painful contact heat stimuli of 51°C with inter-stimulus intervals of 20-60 seconds. fMRI: High-resolution T2*-weighted fMRI (GE-EPI, TR/TE/FA = 1200ms/33.2ms/66°, FOV/matrix = 240x240mm/160x160, number of slices = 60, spatial resolution = 1.5mm isotropic, 600 volumes) was acquired on a MAGNETOM 7T scanner (Siemens Healthcare, Erlangen, Germany) with a single-channel-transmit/32-channel receive head coil (Nova Medical, Wilmington, MA, USA). Data analysis: Preprocessing was performed using fMRIPrep, SANLM filtering via the CAT12 toolbox4 in SPM12 at three strengths: light, medium, and strong. Gaussian smoothing was carried out at 3.75 mm and 2.3 mm full width at half maximum (FWHM) with AFNI’s 3dmerge, corresponding to 2.5- and 1.5-voxel FWHM. FSL FEAT was used for first level analysis by generalized linear model regression, and for calculating intrinsic smoothness of the 4D data. tSNR maps were created via AFNI’s 3dtstat, noise standard deviation maps in MatLab by computing the standard deviation over the time axis after removing correlated signal changes from the dataset using singular value decomposition and discarding the first 50 of 600 singular vectors.Results
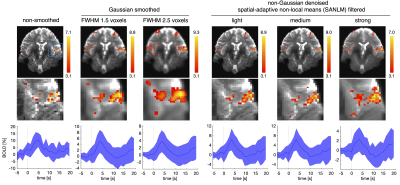
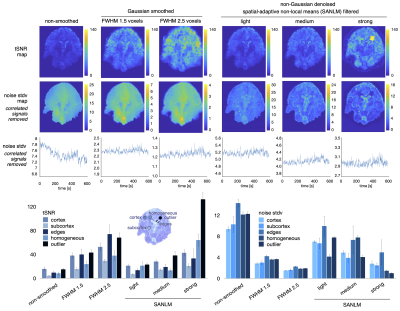
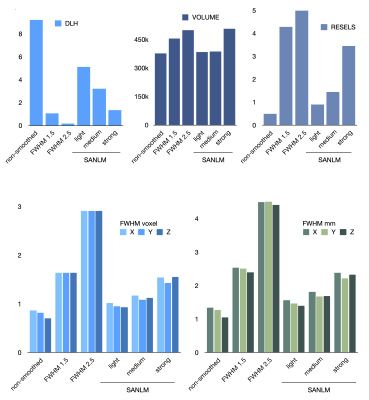
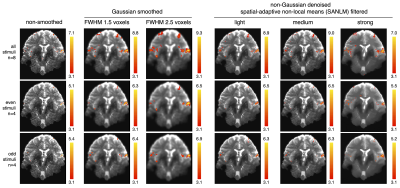
Gaussian smoothing amplifies the BOLD effect, but it also blurs the spatial details of BOLD clusters. This becomes apparent when comparing fMRI data Gaussian-smoothed at standard (FWHMvoxel2.5) and reduced (FWHMvoxel1.5) kernel size versus non-smoothed data (Fig. 1). SANLM filtered data (especially with strong SANLM) show an amplification of BOLD effects, comparable to the reduced smoothing kernel, while preserving spatial features of BOLD clusters. The increased sensitivity to BOLD effects in smoothed and SANLM filtered data corresponds to a successive increase in tSNR with increasing kernel size and filter strength (Figure 2). However, the noise distribution becomes successively heterogeneous with increasing SANLM filter strength; SANLM filtering suppresses noise in homogeneous areas, while noise variance remains higher at anatomical edges (Figure 2). The overall intrinsic smoothness of the data that was treated with the strong SANLM filter corresponds to data smoothed with a Gaussian kernel of reduced size, both comprising an intrinsic smoothness of approximately 1.6 voxels FWHM (Figure 3). BOLD patterns in response to each of two sets of heat stimuli (a total of 8 successive stimuli, grouped into 4 odd and 4 even stimuli) showed reasonable test-retest reproducibility for both smoothed and SANLM-filtered conditions (Figure 4).Discussion & Conclusion
SANLM denoising may be an appealing alternative to Gaussian smoothing in order to preserve fine-grained spatial details in fMRI, especially at UHF. Nevertheless, it should be employed with caution as its spatial detail is partially driven by the underlying anatomy. Since SANLM removes noise in homogeneous areas while maintaining edges, it prevents the spread of BOLD patterns between adjacent structures (e.g., grey matter along gyri or subcortical nuclei), provided there is a discernible contrast separating the structures. This could help unambiguously identify activated regions, which may be a useful asset for fMRI. In regions that comprise very low structural contrast SANLM filtering smoothes details and increases SNR similarly to a Gaussian kernel size of 1.5 voxels FWHM. For SANLM-denoised data it remains to be established under which circumstances the criteria of RFT are met to adjust cluster-defining thresholds, depending on the non-uniformity of smoothness of the resulting z-maps5,6. This is a topic for further investigation, to make a direct comparison with spatially-adaptive smoothing of z-maps instead of single volumes, in order to avoid guidance by structural contrast7, with the ultimate goal of better preserving fine-grained spatial details en route to identifying pain-specific functional neurosignatures via fMRI at 7T.Acknowledgements
No acknowledgement found.References
1. Manjón JV, Coupé P, Martí-Bonmatí L, et al. Adaptive non-local means denoising of MR images with spatially varying noise levels. JMRI. 2010;31(1)192-203.
2. Bernier M, Chamberland M, Houde JC, et al. Using fMRI non-local means denoising to uncover activation in sub-cortical structures at 1.5 T for guided HARDI tractography. Front Hum Neurosci. 2014;11(8):715.
3. Worsley K J, Marrett S, Neelin P, Vandal AC et al. A unified statistical approach for determining significant signals in images of cerebral activation. Human brain mapping. 1996;4(1):58–73.
4. Gaser C, Dahnke R, Kurth K, et al. A Computational Anatomy Toolbox for the Analysis of Structural MRI Data. http://www.neuro.uni-jena.de/cat12-html/cat.html
5. Hayasaka S, Nichols TE. Validating cluster size inference: random field and permutation methods. Neuroimage. 2003;20(4):2343-56.
6. Woo CW, Krishnan A, Wager TD. Cluster-extent based thresholding in fMRI analyses: pitfalls and recommendations. Neuroimage. 2014;91:412-9.
7. Welvaert M, Tabelow K, Seurinck R, Rosseel Y. Adaptive smoothing as inference strategy: more specificity for unequally sized or neighbouring regions. Neuroinformatics. 2013;11(4):435-45.
Figures
Figure 1. Comparison of BOLD responses to brief painful heat stimuli at cluster-level inference (p<0.05) with different smoothing: Gaussian smoothing at standard (FWHMvoxel2.5) and reduced (FWHMvoxel1.5) kernel size amplifies BOLD effect, but blurs the spatial details of BOLD clusters. Data denoised with strong SANLM filter yields BOLD amplification similar to FWHMvoxel1.5, while exhibiting more spatial detail. BOLD time series shows a second peak at around 20 s, which is characteristic for late c-fiber transduction of nociceptive signals to the brain ("2nd pain“).
Figure 2. tSNR, and noise standard deviation over the time after removing correlated signal changes via singular value decomposition, discarding the first 50 singular vectors. Standard deviation over the time is plotted as mean of the entire brain volume. SNR increases (and noise variance decreases accordingly) with SANLM filer strength and Gaussian smoothing kernel. Note that after removing correlated signal changes, Gaussian smoothing increases SNR equally irrespective of the structure, while SANLM filters improve SNR in anatomical edges more than in homogeneous areas.
Figure 3. Intrinsic smoothness of data denoised with Gaussian smoothing versus SANLM. Determinant half-power lambda (DLH) – which is the natural parameterization of roughness from RFT – for the strong SANLM approximates those of data smoothed with a Gaussian kernel size FWHM at 1.5. Resolution elements (RESELS) for SANLM were slightly lower. The intrinsic smoothness calculated for strong SANLM – measured as FWHM(x,y,z) – also approximates that of data smoothed with a reduced Gaussian kernel. An FWHM of about twice the voxel size ensures the validity of Gaussian RFT.
Figure 4. Reproducibility of BOLD patterns. BOLD patterns in response to each of two sets of heat stimuli (a total of 8 successive stimuli, grouped into 4 odd and 4 even stimuli) showed reasonable test-retest reproducibility for both smoothed and SANLM-filtered conditions.
DOI: https://doi.org/10.58530/2022/1098