1061

Single-Shot Adaptation using Score-Based Models for MRI Reconstruction

Marius Arvinte¹, Ajil Jalal¹, Giannis Daras², Eric Price², Alex Dimakis¹, and Jonathan I Tamir^1,3,4
¹Electrical and Computer Engineering, The University of Texas at Austin, Austin, TX, United States, ²Computer Science, The University of Texas at Austin, Austin, TX, United States, ³Oden Institute for Computational Engineering and Sciences, The University of Texas at Austin, Austin, TX, United States, ⁴Diagnostic Medicine, Dell Medical School, The University of Texas at Austin, Austin, TX, United States

Synopsis

This work deals with the problem of few-shot adaptation in data-driven MRI reconstruction, where models must efficiently adapt to new distributions. We introduce score-based models for MRI reconstruction and an algorithm for adjusting inference parameters (step size, noise level and stopping point), investigate the impact of these parameters on reconstruction performance, and demonstrate average gains of at least 2 dB in PSNR across a range of acceleration values, all while using a pretrained model that was trained for brain MRI and fine-tuned using only a single fully-sampled 2D knee scan from the fastMRI database.

Introduction

Multi-coil MRI reconstruction$$$^1$$$ has seen significant improvements when using methods from both compressed sensing$$$^{2,3,4}$$$, as well as data-driven approaches, in particular in the form of deep neural networks trained with$$$^{5,6,7,8}$$$ or without$$$^{9,10}$$$ supervision. While the performance of these approaches is understood in situations where test conditions match training (e.g., same anatomy and contrast), there are open problems on how to develop robust data-driven methods that perform well under severe domain shifts$$$^{11,12,13}$$$.

Score-based models$$$^{14,15}$$$ have recently emerged as a promising research direction$$$^{16,17,18,19}$$$, with recent work$$$^{16}$$$ showing that the approach is competitive with end-to-end models that assume fixed measurement conditions and incurs small performance losses under distributional shifts, without any adjustments. However, there remains an open question on how to efficiently adjust inference parameters when the shift is severe and performance degradation does occur. Score-based models offer an efficient way of tuning a small set of hyper-parameters, while retaining the representational power of deep neural networks.

Our contributions are: (i) we introduce a single-shot adaptation method developed specifically for inference using score-based models; and (ii) we investigate the influence of hyper-parameters on reconstruction performance and demonstrate that the proposed approach can improve reconstruction of knee scans when using a model pre-trained exclusively on brain scans.

Methods

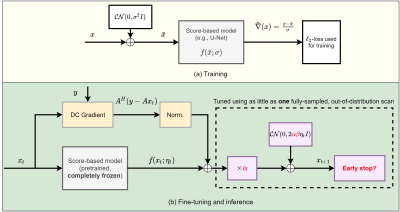
The core component of our work is a score-based model$$$^{14}$$$ for multi-coil MRI reconstruction. This model takes as input complex-valued images$$$\,x\,$$$and outputs estimates for the gradient of the log-likelihood of$$$\,p_X(x)$$$, the natural distribution of$$$\,x.\,$$$In this work, we use noise-conditional models$$$^{15}$$$. An overview of training is shown in Fig.1(a), with complete details available in prior work$$$^{16}$$$. Once$$$\,f(x)\,$$$is learned on the training distribution, inference is done by formulating MRI reconstruction as a posterior sampling problem. Given measurements$$$\,y\,$$$obtained as$$$\,y=Ax+n$$$, where$$$\,A\,$$$is the multi-coil MRI forward model and$$$\,n\,$$$is assumed to be Gaussian i.i.d., our goal is to solve the inverse problem by sampling from the posterior distribution:$$p(x|y)\propto{p(y|x)p_X(x)}.$$Because$$$\,p_X(x)\,$$$is intractable and cannot be easily sampled from, we leverage that the score-based model directly outputs an estimate for the gradient of$$$\,\log{p_X(x)}\,$$$and use annealed Langevin dynamics$$$^{14,20}$$$ with the update at step$$$\,t\,$$$given by:$$x_{t+1}\leftarrow x_t+\alpha\eta_t\big(f(x_t;\eta_t)+\textrm{norm}(A^H(y-Ax_t))\big)+\sqrt{2\beta\alpha\eta_t}z_t.$$The number of steps$$$\,N\,$$$and$$$\,\alpha,\beta\,$$$and$$$\,\eta_t\,$$$are hyperparameters.$$$\,\alpha\,$$$represents the step size and$$$\,\beta\,$$$represents an independent multiplicative factor for the added noise. $$$\textrm{norm}$$$ is an $$$\ell_2$$$-normalization operator that balances the magnitude of the gradient terms, and $$$z_t$$$ is Gaussian noise sampled at each step. An example of the reconstruction output at different stages is animated in Fig.2. Inference starts with$$$\,x_0\,$$$drawn uniformly at random and proceeds for $$$N$$$ steps. $$$\eta_t\,$$$is geometrically decreased with a fixed rate. Given a trained score model $$$f$$$, a measurement model$$$\,A\,$$$and a single, fully-sampled image$$$\,x$$$, we introduce the following single-shot adaptation algorithm:$$\textrm{argmax}_{\alpha,\beta,N}\textrm{PSNR}(x,x_N(\alpha,\beta,A,f)).$$That is, we want to find hyper-parameters $$$\alpha,\beta,N$$$ that have the best reconstruction peak signal-to-noise ratio (PSNR). In practice, this is intractable since $$$x_N$$$ involves thousands of passes through the deep neural network$$$\,f$$$. We thus resort to searching among a fixed set of combinations of$$$\,\alpha,\beta\,$$$and all intermediate stopping points. If two sets of parameters lead to the same performance, we choose the solution with smaller $$$N$$$ to accelerate inference.

Results

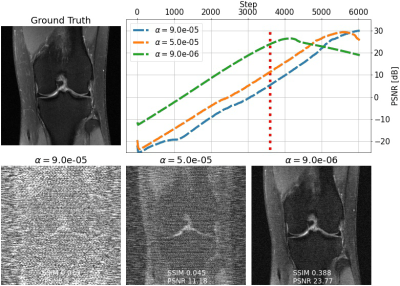
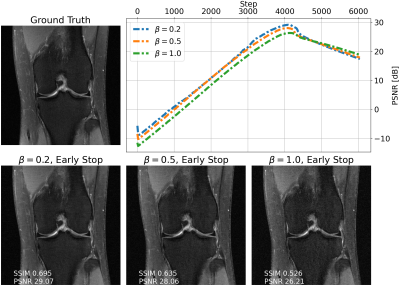
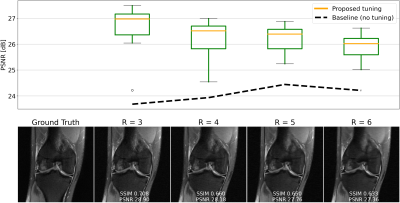
We evaluate single-shot adaptation performance using a pre-trained NCSNv2$$$^{15}$$$score-based model on T2 brain scans, tuned to reconstruct proton density, fat-suppressed knee scans. Training, tuning and test samples are used from the fastMRI database. We train the score-based model using SENSE-combined$$$^1$$$ T2 brain images and sensitivity maps estimated with the ESPIRiT$$$^{4}$$$ algorithm at acceleration$$$\,R=4$$$. As baseline and starting point for the grid search, we consider inference parameters used in prior work$$$^{16}$$$. The exact values are$$$\,\alpha=5e-5,\beta=1, N=6044$$$ steps. We do not tune$$$\,\eta_t\,$$$and instead resort to using the same values used for brain as the default implementation$$$^{16,21}$$$. We use ten knee slices: one (chosen at random) is fully-sampled and used for fine-tuning, while the other nine are used as test. The sampling pattern is randomly selected phase encode lines at$$$\,R=4$$$.

Fig. 2 shows the effect of early stopping and tuning the step size$$$\,\alpha$$$, where it is clear that either of the two is required to prevent overfitting during inference. Interestingly, a smaller step size leads to faster convergence, and this represents our motivation for tuning$$$\,\beta$$$. Fig. 3 shows the impact of reducing$$$\,\beta\,$$$at$$$\,\alpha=9e-6$$$. It can be seen that this leads to better quantitative and qualitative reconstructions, impacting the textural details of the reconstructed image. We use$$$\,\beta=0.2,\alpha=9e-6\,$$$and$$$\,N=4100\,$$$as tuned values for inference, all obtained from the single training scan in Fig. 2 and 3. Test reconstructions with these values are shown in Fig. 4, where it can be seen that the proposed approach always improves over the baseline method that uses default hyper-parameters. Finally, Fig. 5 plots the distribution of the average test PSNR when the sample used for fine-tuning changes, as an additional function of$$$\,R$$$. Even though the hyper-parameters are tuned for$$$\,R = 4$$$, performance is consistent across a range of values, and always superior to the baseline regardless of which sample is used for fine-tuning.

Conclusion

We have introduced an efficient single-shot adaptation algorithm for score-based models. The method can be useful in clinical practice when a large collection of fully-sampled scans from the target domain is not available. Future research directions include evaluating the proposed approach on prospective scans and a rigorous comparison with a wider body of prior work.

Acknowledgements

We thank the following funding sources: NSF IFML 2019844 Award, ONR grant N00014-19-1-2590, NIH Grant U24EB029240, an AWS Machine Learning Research Award, NSF Grants CCF 1763702, 1934932, AF 1901281, 2008710, 2019844, NSF Awards CCF-1751040 and CCF-2008868, gifts by Western Digital, Interdigital, WNCG and MLL, computing resources from TACC and the Archie Straiton Fellowship.

References

[1] Pruessmann, Klaas P., et al. "SENSE: sensitivity encoding for fast MRI." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 42.5 (1999): 952-962.

[2] Lustig, Michael, et al. "Compressed sensing MRI." IEEE signal processing magazine 25.2 (2008): 72-82.

[3] Ying, Leslie, and Jinhua Sheng. "Joint image reconstruction and sensitivity estimation in SENSE (JSENSE)." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 57.6 (2007): 1196-1202.

[4] Uecker, Martin, et al. "ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA." Magnetic resonance in medicine 71.3 (2014): 990-1001.

[5] Arvinte, Marius, et al. "Deep J-Sense: Accelerated MRI Reconstruction via Unrolled Alternating Optimization." Medical Image Computing and Computer Assisted Intervention – MICCAI 2021 (2021): 350-360.

[6] Hammernik, Kerstin, et al. "Learning a variational network for reconstruction of accelerated MRI data." Magnetic resonance in medicine 79.6 (2018): 3055-3071.

[7] Sriram, Anuroop, et al. "End-to-end variational networks for accelerated MRI reconstruction." International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, Cham, 2020.

[8] Aggarwal, Hemant K., Merry P. Mani, and Mathews Jacob. "MoDL: Model-based deep learning architecture for inverse problems." IEEE transactions on medical imaging 38.2 (2018): 394-405.

[9] Cole, Elizabeth K., et al. "Unsupervised MRI reconstruction with generative adversarial networks." arXiv preprint arXiv:2008.13065 (2020).

[10] Desai, Arjun D., et al. "Noise2Recon: A Semi-Supervised Framework for Joint MRI Reconstruction and Denoising." arXiv preprint arXiv:2110.00075 (2021).

[11] Antun, Vegard, et al. "On instabilities of deep learning in image reconstruction and the potential costs of AI." Proceedings of the National Academy of Sciences 117.48 (2020): 30088-30095.

[12] Darestani, Mohammad Zalbagi, Akshay Chaudhari, and Reinhard Heckel. "Measuring Robustness in Deep Learning Based Compressive Sensing." arXiv preprint arXiv:2102.06103 (2021).

[13] Johnson, Patricia M., et al. "Evaluation of the Robustness of Learned MR Image Reconstruction to Systematic Deviations Between Training and Test Data for the Models from the fastMRI Challenge." International Workshop on Machine Learning for Medical Image Reconstruction. Springer, Cham, 2021.

[14] Song, Yang, and Stefano Ermon. "Generative Modeling by Estimating Gradients of the Data Distribution." Proceedings of the 33rd Annual Conference on Neural Information Processing Systems. 2019.

[15] Song, Yang, and Stefano Ermon. "Improved Techniques for Training Score-Based Generative Models." Advances in neural information processing systems (2020).

[16] Jalal, Ajil, et al. "Robust Compressed Sensing MRI with Deep Generative Priors." Proceedings of the 35th Annual Conference on Neural Information Processing Systems (to appear). 2021.

[17] Song, Yang, et al. "Solving Inverse Problems in Medical Imaging with Score-Based Generative Models." NeurIPS 2021 Workshop on Deep Learning and Inverse Problems. 2021.

[18] Quan, Cong, et al. "Homotopic Gradients of Generative Density Priors for MR Image Reconstruction." IEEE Transactions on Medical Imaging (2021).

[19] Chung, Hyungjin. "Score-based diffusion models for accelerated MRI." arXiv preprint arXiv:2110.05243 (2021).

[20] Jalal, Ajil, et al. "Instance-Optimal Compressed Sensing via Posterior Sampling." International Conference on Machine Learning (2021).

[21] https://github.com/utcsilab/csgm-mri-langevin.

Figures

(a) Simplified training flow for the score-based model used for MRI reconstruction. In order to obtain the approximate gradient of log p(x) for training, noise with known variance is added to x, and the model is trained to predict the finite difference approximation of the gradient at the noisy sample. (b) A single inference step, with its multiple components: the score (gradient of the log-likelihood) predicted by the pretrained model, the gradient of the data consistency (DC) term, and the added noise at each step. The hyper-parameters that are tuned in this work are shown in red fonts.

(Animated) Impact of varying step size and early stopping on a fat-suppressed knee validation scan from the fastMRI dataset, at acceleration R=4. The top plot shows the ground truth image and reconstruction PSNR as along the inference. The bottom row shows reconstructed samples at several stopping points, indicated by the vertical red lines. Early stopping provides a considerable improvement in reconstruction, showing the benefit of tuning the stopping point on the target domain. A smaller step size leads to faster convergence, but also comes with a drop in peak performance.

Impact of varying the noise power when used in conjunction with early stopping and a low value of the step size. Similar to Fig. 2, the faster convergence is retained when decreasing the amount of added noise, but a smaller noise level also leads to a quantitative (almost 3 dB) and qualitative improvement of the reconstruction, leading to inference parameters that achieve an efficient trade-off: significantly (33%) faster inference with a slight drop in quantitative (0.9 dB) performance and equivalent qualitative performance.

Randomly chosen test reconstructions using inference parameters tuned with a single fully-sampled, fat-suppressed knee scan from the fastMRI validation set. All results are obtained at acceleration factor R=4, with randomly selected k-space lines. Compared to baseline inference that does not tune parameters, the proposed single-shot adaptation approach successfully removes more of the aliasing artifacts, improves quantitative scores and recovers accurate details in the meniscus region, shown in the orange insets.

Ten-fold cross-validation performance of the proposed approach when a single sample is used to determine the inference parameters. The plot shows the distribution of the average reconstruction PSNR across the ten folds and at different accelerations. The bottom shows exemplar test reconstructions across the range of R. This result shows the robustness of the proposed approach w.r.t. the variation present in the sample used for fine-tuning, as well as the robustness to the acceleration R, since parameters are tuned only for R=4.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

1061

DOI: https://doi.org/10.58530/2022/1061