1055

Concept of a symmetry-guided single-layer neural network for image reconstruction of undersampled radial-MRI k-space data.

Sjoerd Ypma¹, Ivo Maatman¹, Matthan Caan², Dimitris Karkalousos², Marnix Maas¹, and Tom Scheenen¹
¹Radboud UMC, Radiology and Nuclear Medicine, University of Nijmegen, Nijmegen, Netherlands, ²Amsterdam UMC, Biomedical Engineering and Physics, University of Amsterdam, Amsterdam, Netherlands

Synopsis

Undersampled k-space data reconstruction results in aliasing artifacts. Compressed sensing theory enables image reconstruction by using a priori knowledge in the form of regularization. Increasingly, Machine Learning methods are used to learn the regularization from data itself, but these methods can result in unstable reconstructions.

We propose a translation equivariant single-layer neural network for reconstruction of radially measured k-space data. By exploiting translation symmetry, it can learn from randomly simulated data while still being applicable to in-vivo measurements. We tested robustness to small perturbations and reliability of the reconstruction of unexpected objects.

Introduction

Accelerating MRI by undersampled acquisition combined with advanced image reconstruction has been a focus of MRI research for decades. This has resulted in the widespread adoption of parallel imaging and, more recently, compressed sensing (CS)¹ methods. Machine learning is increasingly used to reconstruct images from undersampled k-space data² as, contrary to CS, it does not need an a priori determined regularization term. Unfortunately, this commonly results in unstable methods for image reconstruction³.

We propose the use of geometric deep learning principles⁴ to define a translation equivariant single-layer neural network that reconstructs images from undersampled radial stack-of-stars⁵ k-space data. This approach reduces the model size needed for reconstruction and amount of training examples needed for learning.

Theory

After applying the inverse fast Fourier transform (iFFT) along the partition direction of the measured 3D k-space data, each k-space slice was used as input for the Projection-Layer ($$$P$$$), and subsequently coil-combined by using the sum-of-squares method.

The Projection-Layer is designed to be translation equivariant. It contains a set of complex-valued weights and is trained to generate the single complex pixel value $$$S_{00}$$$ corresponding to the origin-pixel of the image $$$S$$$: $$S_{00} = \sigma\left(\sum_{M,N}W_{mn}K_{mn}\right)$$

where $$$K \in \mathbb{C}^{M \times N}, W \in \mathbb{C}^{M \times N}, M, N$$$ and $$$\sigma$$$ are the measured k-space, weights, number of spokes, number of readout points and activation function respectively. The activation function is chosen to be a tanh-function on both the real and imaginary part of the output separately. The implementation of this complex-valued multiplication is explained in Figure 1. Note that if $$$K$$$ would be fully sampled Cartesian, $$$W_{m,n} = 1$$$ for all $$$m,n$$$.

Pixels $$$S_{xy} \in S$$$ outside the image origin are reconstructed by first shifting them to the origin, which is achieved by applying a specific linear phase shift to every readout in k-space (Figure 2). According to the Fourier shift theorem we find: $$S_{xy} = \sigma\left(\sum_{M,N}W_{mn}K_{mn}e^{-im\Delta x'}\right) \equiv \sigma\left(\sum_{M,N}P_{mn}(x,y)K_{mn}\right)$$
With $$$\Delta x' = r\cos\left(\theta-\phi_n\right), r = \sqrt{x^2+y^2}, \theta = \tan^{-1}\left(\frac{x}{y}\right)$$$ and $$$\phi_n$$$ the angle of the $$$n$$$^th spoke. Looping over all pixels results in the output image.

Methods

The network was trained on 60 randomly generated images combined with 8 randomly generated coil sensitivity maps resulting in 480 different complex images. Simulated k-space data of 32 spokes and 256 readout points was generated by applying the non-uniform FFT (NUFFT).⁶ The validation set was created using the same method but with a different base image (Figure 3). As loss function for training the network we chose the mean squared error.

Furthermore, the network’s performance was tested on a phantom and an in-vivo breath-hold scan acquired on a 3T MR-scanner (MAGNETOM Prisma-Fit, Siemens Healthcare, Erlangen, Germany) (Table 1). Output images were compared to NUFFT and CS reconstructions with 2D-spatial total variation (TV) constraint ($$$\lambda=0.01$$$). The robustness and stability of the reconstructions were verified by retrospectively adding Gaussian noise to the radial k-space data and by digitally adding a screw into the in-vivo data.

Results

The Projection-Layer had roughly 32K trainable parameters and converged to an optimum after only 120 iterations, learning to reconstruct undersampled 2D golden-angle radial k-space data and to suppress streaking artefacts (Figure 3).

Although the network was trained on simulated data of completely different structures, it was able to reconstruct the in-vivo and phantom k-space data into meaningful images (Figure 3). The Projection-Layer reconstructions showed less streaking artifacts at the cost of slightly reduced sharpness compared to CS and NUFFT images.

The Projection-Layer reconstruction had increased robustness against added noise compared to CS and NUFFT reconstructions, and accurately reconstructed the digitally added screw (albeit with reduced sharpness, similar to the rest of the image), suggesting robustness for small perturbations in the input and reliable reconstruction of unexpected objects (Figure 4).

Discussion

This work investigates a new concept for machine-learning based radial MRI reconstruction, using a translation equivariant single-layer network. Initial results suggest that reliable reconstructions robust to small perturbations of the input data can be achieved with a low number of trainable parameters. A significant advantage of this method is that it can be trained completely on simulated data, eliminating the need for large measured training data sets.

This technique exploits the property that points perpendicular to spoke orientations are projected onto the corresponding readout point. Therefore, it heavily depends on the readout resolution as this determines the precision of the localisation of the pixel value in the resulting image. The error on the true pixel intensity is mainly dependent on the number of spokes used to reconstruct the image.

The first implementation of our Projection-Layer leaves room for improvement. Commonly, it is more effective to learn local features that combine to global features through the use of multiple layers. This could also improve our results.

Conclusion

The concept of a translation equivariant single-layer neural network for reconstruction of radially measured k-space data provides a stable and robust reconstruction technique. With very few trainable parameters, it is able to train on randomly simulated data while being applicable to in-vivo measured k-space data. The defined network suggest robustness to small perturbations and is able to reconstruct unexpected objects.

Acknowledgements

not applicable.

References

Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182-1195. doi:10.1002/mrm.21391
Lundervold AS, Lundervold A. An overview of deep learning in medical imaging focusing on MRI. Z Med Phys. 2019;29(2):102-127. doi:10.1016/j.zemedi.2018.11.002
Antun V, Renna F, Poon C, Adcock B, Hansen AC. On instabilities of deep learning in image reconstruction and the potential costs of AI. Proc Natl Acad Sci U S A. 2020;117(48):30088-30095. doi:10.1073/pnas.1907377117
Bronstein MM, Bruna J, Cohen T, Veličković P. Geometric Deep Learning: Grids, Groups, Graphs, Geodesics, and Gauges. Published online 2021. http://arxiv.org/abs/2104.13478
Block KT, Uecker M, Frahm J. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magn Reson Med. 2007;57(6):1086-1098. doi:10.1002/mrm.21236
Uecker M, Holme C, Blumenthal M, et al. mrirecon/bart: version 0.7.00. Published online March 1, 2021. doi:10.5281/ZENODO.4570601

Figures

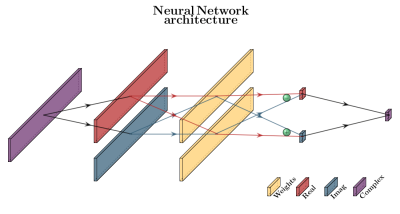
Figure 1: Design of the Projection layer. The input is first split into real (red line) and imaginary (blue line) parts. These are pointwise multiplied and summed into a real and imaginary output and combined into the complex output. Therefore, given a complex input $$$K = \color{red}{\alpha} +i\color{blue}{\beta}$$$ and weights $$$W = \color{red}{a} +i\color{blue}{b}$$$ , the output is $$$\sum (\color{red}{a\alpha}-\color{blue}{b\beta})+i\sum (\color{red}{\alpha}\color{blue}{b}+\color{blue}{\beta}\color{red}{a})$$$ .

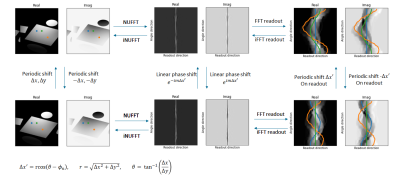
Figure 2: Overview of how a shift operation in Cartesian image affects radial k-space data. Left: the real and imaginary part of a simulated phantom with three reference points, right: their corresponding sinograms. Middel: Shifting the sinograms is equivalent to linear phase shifting the k-space data. $$$m,\phi_n$$$ are respectively the readout position and angle of the $$$n$$$^th spoke.

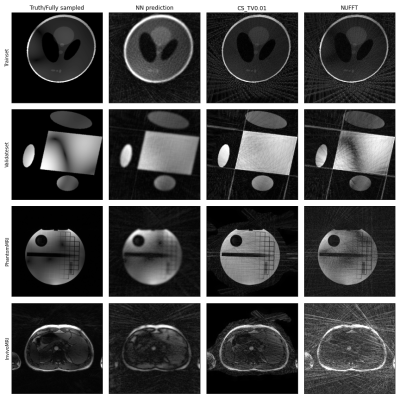
Figure 3: First row: the simulated training set, second row: the simulated validation set, third row: the measured phantom scan, fourth row: the measured in-vivo scan. Left to right: Reference image from which the k-space is simulated or fully sampled images, Projection-Layer reconstruction, Compressed Sensing reconstruction with spatial total variation constraint ( $$$\lambda = 0.01$$$) , non-uniform Fourier transform reconstruction. All reconstructions were done on 13x undersampled data.

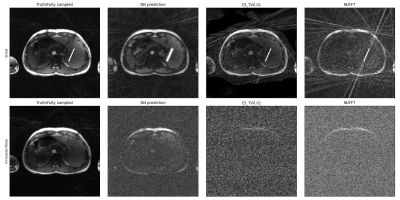
Figure 4: Effect of adding a simulated screw (first row) and additional gaussian noise (second row) to the in-vivo scan. Left to right: Fully sampled NUFFT reconstructions, reconstructions of 13x undersampled data using the Projection-Layer, Compressed Sensing with a spatial total variation constraint ($$$\lambda = 0.01$$$) and non-uniform Fourier transform respectively.

Table 1: 3T sequence parameters for phantom and in-vivo breath-hold acquisitions.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

1055

DOI: https://doi.org/10.58530/2022/1055