Introduction

In clinical routine, MRI scan-time reduction is commonly achieved by Parallel Imaging methods, typically based on uniform k-space sub-sampling and simultaneous signal reception with multiple receiver coils. The GRAPPA¹ method interpolates missing k-space signals by linear-combination of adjacent, acquired signals across all channels, and can be described by a linear convolution in k-space. Recently, a more generalized method called RAKI² was introduced. RAKI is a deep-learning method that generalizes GRAPPA with additional convolution layers, on which a non-linear activation function is applied. This enables non-linear estimation of missing signals by convolutional neural networks (CNNs). In analogy to GRAPPA, the convolution kernels in RAKI are trained using scan-specific training samples, which are obtained from auto-calibration-signals (ACS). RAKI provides superior reconstruction quality in comparison to GRAPPA, however, often requires much more ACS due to its increased number of unknown parameters. In order to overcome this limitation, an iterative k-space interpolation approach (Iterative RAKI) is proposed.

Methods

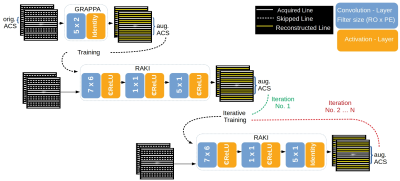
RAKI: Two major modifications were made in comparison to the original implementation²: In order to avoid that the mathematical correlation is dismissed between real-and imaginary-part of k-space data, we implemented complex-valued convolutions instead of its real-valued counterpart within the CNN^3,4. Furthermore, to yield a time benefit in training, we implemented one single CNN for simultaneous multi-coil k-space interpolation, instead of assigning each coil one CNN.
Iterative RAKI: An initial GRAPPA reconstruction is performed using a small fully sampled central k-space region (8%) as original ACS to obtain augmented training data of increased size for RAKI training, and to allow for increasing the filter-size assigned to the first convolution layer in the CNN^5,6 from 5x2 to 7x6 (readout RO x phase encoding PE), respectively (Fig. 1). Augmented training data is extracted from N=100 central lines of the initial GRAPPA k-space reconstruction. Subsequent iterations follow in which the CNN weights are transferred, and further optimized using N’=100 central lines from the RAKI reconstruction of the previous iteration as training data (orig. ACS re-inserted at each iteration). The learning rate η is decreased by ∆η after each iteration (initial value η₀=0.05, ∆η=0.003 for R=4 and 0.004 for R=5, R: undersampling-rate). Complex ReLU⁷ is chosen as activation, and the mean-squared-error as cost function. Coil-images are combined using root-sum-of-squares.
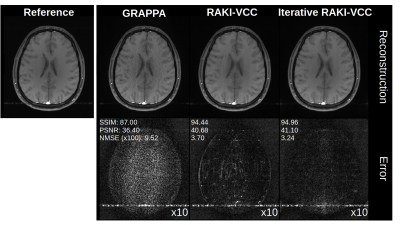
In-vivo Experiments (Variable density acquisition-scheme): 2D brain imaging was acquired on healthy volunteer at 3T (Magnetom Skyra, Siemens Healthineers) using T1-weighted TSE (TR/TE=500/10 ms, FOV=220x193 mm² (ROxPE), matrix-size= 256x224, 16 receiver-coils). Additionally, a FLAIR dataset from the fastMRI⁸ neuro database is considered (TSE, TR/TE=9000/181 ms, Inv.-Time 2500 ms, FOV=220x220 mm², matrix-size 320x320, 16 receiver-coils). Both datasets were retrospectively undersampled, and 8% of total number of phase-encoding lines at k-space center were used as original ACS. Phase-constrained Iterative RAKI was also tested using the VCC-concept⁹, where additional virtual coils are generated from conjugate-symmetric k-space signals of actual coils. Thereby, additional image- and coil-phase information can be incorporated into the k-space reconstruction process.
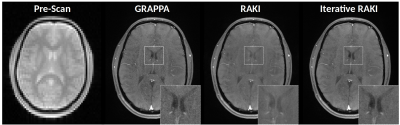
In-vivo Experiments (Pre-scan calibration): To investigate the performance of Iterative RAKI on strongly varying contrast information between training– and undersampled-data5, a proton-density weighted pre-scan of size 64x64 (ROxPE) was acquired, which served as training data for GRAPPA, RAKI and Iterative RAKI. The calibrated models were then used to reconstruct a subsequently acquired, 4-fold undersampled brain-scan (T1-weighted FLASH, TR/TE=250/3.1ms, FOV=250x195 mm², matrix-size 320x260, 16 receiver-coils). Note that as the training data is no integral part of the image scan, it is not re-inserted into reconstructed k-spaces.

Results

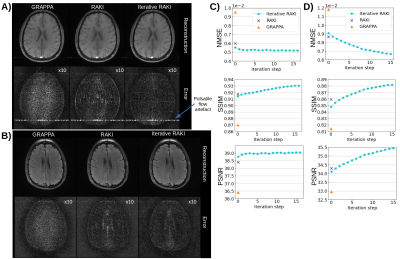
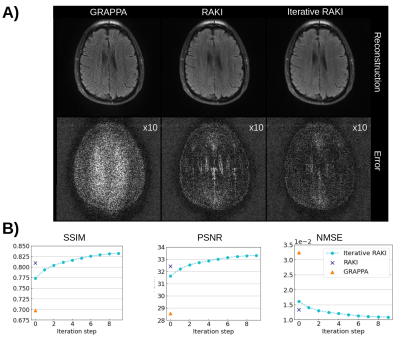
Using only 18 ACS lines (8%) for the T1-dataset at R=4, Iterative RAKI outperforms standard RAKI by suppressing severe residual artefacts, while preserving its g-factor noise-resilience regarding GRAPPA (Fig.2A). This is observed for the FLAIR fastMRI dataset using 26 ACS lines (8%), too (Fig.2B). The enhanced performance is also indicated by the quantitative image quality metrics NMSE, PSNR, and SSIM (Fig.2C and D). Similar results are obtained at R=5 for the FLAIR dataset (Fig.3). Phase-constrained Iterative RAKI yields a strongly enhanced noise-suppression for the T1-dataset at R=4 (Fig.4), while phase-constrained standard RAKI suffers from residual artefacts. In the pre-scan calibration, standard RAKI shows contrast-loss artefacts (Fig.5), which are not present in Iterative RAKI. Moreover, Iterative RAKI shows suppression of GRAPPA g-factor noise enhancement in this case, too.

Discussion

Iterative RAKI outperforms RAKI in standard 2D imaging given a limited training data amount at medium acceleration factors. It combines beneficial features both from GRAPPA and standard RAKI, as it suppresses g-factor noise enhancement in GRAPPA, as well as severe residual artefacts apparent in standard RAKI. The iterative approach includes training data augmentation with GRAPPA, which has been proposed², but not demonstrated. As it is a scan-specific approach, it should prevent hallucination-artefacts, which may occur when neural networks are trained on large multi-image databases for image-reconstruction. For the T1-dataset, phase-constrained Iterative RAKI yields further enhanced reconstruction quality, however, it may be limited in its applicability, since it requires consistent k-space information to avoid residual artefacts.

Conclusion

The number and contrast of ACS is essential for standard RAKI reconstruction quality. For limited training data amount, Iterative RAKI combines beneficial features of GRAPPA and standard RAKI to yield improved reconstruction quality, for training data with strongly varying contrast information, too.

Acknowledgements

The authors thank dataSphere from University of Würzburg for informative discussions and the German Federal Ministry of Education and Research (BMBF) for funding projectline VIP+ (03VP04951).