1052

A data-driven method for automatic regularization selection in a hybrid DL-SENSE reconstruction

Zahra Hosseini¹, Thorsten Feiweier², John Conklin³, Stephan Kannengiesser², Marcel Dominik Nickel², Min Lang³, Azadeh Tabari³, Augusto Lio Concalves Filho³, Wei-Ching Lo⁴, Maria Gabriela Figueiro Longo³, Michael Lev³, Pamela Schaefer³, Otto Rapalino³, Susie Huang³, Stephen Cauley⁵, and Bryan Clifford⁴
¹MR R&D Collaboration, Siemens Medical Solutions USA, Atlanta, GA, United States, ²Siemens Healthcare GmbH, Erlangen, Germany, ³Department of Radiology, Massachusetts General Hospital, Boston, MA, United States, ⁴MR R&D Collaboration, Siemens Medical Solutions USA, Boston, MA, United States, ⁵Department of Radiology, A. A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Harvard Medical School, Boston, MA, United States

Synopsis

The integration of deep learning priors into regularized CG-SENSE reconstructions enables high quality MR images to be generated from noisy, undersampled data. The regularization parameter in these methods can be tuned to control the level of denoising, allowing a network to generalize to novel SNR conditions without retraining. However, manual tuning of the regularization parameter can be time consuming. This work presents a data-driven method for automatic regularization selection using commonly acquired noise calibration data. Results indicate the method generalizes across clinically relevant imaging scenarios and provides diagnostically equivalent image quality to that obtained by manual parameter tuning.

Introduction

Nonlinear image reconstruction methods integrating parallel imaging techniques [1,2] with hand-picked or learned image priors have provided dramatic reductions in imaging time by enabling high-quality images to be reconstructed from noisy, undersampled data [3-9]. Many of these methods include a hyperparameter, called the regularization parameter, that controls the tradeoff between data fidelity and the level of noise/artifact reduction. By tuning this parameter, the same reconstruction algorithm can be adapted to various imaging conditions – a feature which is particularly advantageous when direct adaptation of the image priors is costly. However, manual tuning of the regularization parameter can be time-consuming. Different parameter values may be required for each imaging scenario, and small modifications to the acquisition (e.g., changes in receive coil, resolution, TR/TE, etc.), common in clinical environments, may require additional tuning.

While a large body of research has been dedicated to the automatic selection of regularization parameters [10-15], many methods are computationally intensive or make specific assumptions about the image prior. In this work, motivated by the recent success of learning-based methods in image reconstruction [5-9] and regularization parameter selection [14-16], we present a fast, data-driven method for automatic regularization selection in a hybrid DL-SENSE reconstruction [9].

Methods

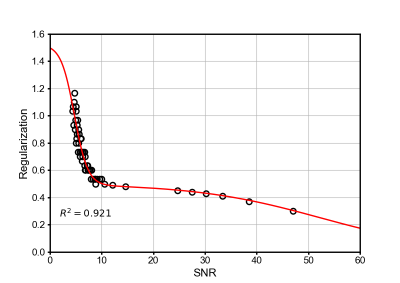
The proposed method learned to select the regularization parameter ($$$\lambda$$$) from an initial estimate of the signal-to-noise ratio (SNR). Specifically, we modeled the mapping from SNR to $$$\lambda$$$ using a sigmoid basis, i.e., $$\lambda(s) = \sum_{\ell=1}^{L} \frac{a_{\ell}}{1+\exp\{-(s-s_{\ell})/b_{\ell}\}} + c,$$ where $$$s$$$ is the SNR, $$$L$$$ is the model order, $$$a_{\ell}$$$, $$$b_{\ell}$$$ and $$$s_{\ell}$$$ are the model parameters, and $$$c$$$ is a normalization constant chosen such that $$$\lambda(\infty) = 0$$$.

This model was applied to a hybrid DL-SENSE reconstruction [9], which reconstructed images by solving the following regularized least-squares problem: $$\min_{\rho}||\mathbf{d} - \Omega\mathrm{FC} \mathbf{\rho}||_{2}^{2} + \lambda||\mathrm{WFC}(\mathbf{\rho}_{\mathrm{net}} -\mathbf{\rho})||_{2}^{2},$$ where $$$\mathbf{d}$$$ and $$$\mathbf{\rho}$$$ are the data and image vectors, respectively; $$$\mathbf{\rho}_{\mathrm{net}}$$$ is an initial reconstructed image generated by a trained deep neural network; $$$\Omega$$$, $$$\mathrm{F}$$$, and $$$\mathrm{C}$$$ are the sampling, Fourier transform, and coil-sensitivity operators, respectively; $$$\mathrm{W}$$$ is a pre-determined diagonal weighting matrix chosen to limit the effect of the network prior to unmeasured k-space locations.

The model parameters were determined by fitting the proposed model to training data acquired with various imaging contrasts, undersampling factors, and noise levels using a custom, non-linear optimization routine. For each training dataset, a ground-truth value of $$$\lambda$$$ was determined through manual-tuning, and SNR was computed as the ratio of the mean image intensity to noise standard deviation. Noise standard deviation was computed from a rapid noise-calibration scan routinely acquired for noise decorrelation prior to image acquisition [17]. Mean image intensity was estimated from an initial SENSE reconstruction after foreground segmentation via k-means clustering. Figure 1 shows the resulting model fit with $$$L=2$$$.

Data from two healthy volunteers and five patients with pathologies were acquired on a 3T system (MAGNETOM Prisma, Siemens Healthcare, Erlangen, Germany) using a 20-channel head-neck coil and a prototype multi-shot, multi-contrast (T1w, T2w, T2* and FLAIR) acquisition [9] in accordance with the local IRB and HIPAA. Raw data for each contrast were reconstructed once using manually tuned regularization parameters (determined by averaging the preferred values of four expert readers), and once with the auto-selected values. All clinical image pairs were subsequently assessed by two board-certified neuroradiologists, blinded to the underlying reconstruction method.

Results and Discussion

Neuroradiologist evaluation of T1w, T2w, T2*, and FLAIR data indicated that images reconstructed using the automatically selected regularization parameters had diagnostically equivalent image quality compared to images reconstructed using manually tuned regularization parameters. Figure 2 shows representative reconstructions for a patient with cerebral atrophy and findings of chronic cerebral small vessel disease (leukoaraiosis). While it took an average of approximately 1 hour for each of the evaluators to tune the regularization parameters for each contrast, the proposed method took place during the reconstruction itself without a noticeable increase in reconstruction time.

The benefit of auto-regularization was particularly evident when protocol parameters deviated from those used during manual tuning. For instance, when regularization parameters manually tuned for acceleration factors R=2 were used for R=3-4, the resulting reconstructions had increased noise, which obscured fine details in the image (Figure 3). Similarly, when the regularization parameter tuned to work with 4 mm thick slices was used with thinner or thicker slices, it led to noisy or overly smooth reconstructions, respectively (Figure 4). In contrast, the proposed auto-regularization method was able to adapt to these protocol changes and provided more consistent image quality in both scenarios.

Conclusion

We proposed a novel, data-driven method for automatic regularization selection in a hybrid DL-SENSE reconstruction. Neuroradiologist evaluation indicated that the method provided diagnostically equivalent image quality to that obtained through time-consuming manual parameter optimization, and results from volunteer data demonstrated that the method could successfully adapt to changes in acquisition parameters.

Acknowledgements

The work was funded by the National Institutes of Health (P41EB030006), an RSNA Seed Grant, and research grants from Siemens Healthineers.

References

[1] Griswold, M.A., et al., "Generalized autocalibrating partially parallel acquisition (GRAPPA)". Magn Reson Med. 2002;47:1202-1210.
[2] Pruessmann K.P., et al., "SENSE: Sensitivity encoding for fast MRI", Magn Reson Med. 1999;42:952-962.
[3] Liang D, et al., "Accelerating SENSE using compressed sensing: Compressed Sensing SENSE", Magn Reson Med. 2009;62(6):1574-1584.
[4] Mussard E, et al., "Accelerated MP2RAGE imaging using Cartesian phyllotaxis readout and compressed sensing reconstruction", Magn Reson Med. March 2020:mrm.28244.
[5] Hammernik K, et al., "Systematic evaluation of iterative deep neural networks for fast parallel MRI reconstruction with sensitivity‐weighted coil combination", Magn Reson Med. 2021;86(4):1859-1872.
[6] Schlemper J, et al., "A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction", IEEE Trans Med Imaging. 2018;37(2):491-503.
[7] Kim TH, Garg P, Haldar JP. LORAKI, "Autocalibrated Recurrent Neural Networks for Autoregressive MRI Reconstruction in k-Space", arXiv:190409390 [cs, eess]. April 2019. http://arxiv.org/abs/1904.09390. Accessed July 11, 2019.
[8] Eo T, et al., "KIKI‐net: cross‐domain convolutional neural networks for reconstructing undersampled magnetic resonance images", Magn Reson Med. 2018;80(5):2188-2201.
[9] Clifford, B., et al., "Clinical evaluation of an AI-accelerated two-minute multi-shot EPI protocol for comprehensive high-quality brain imaging", in proceeding of International Society of Magnetic Resonance in Medicine (2021).
[10] Hansen, P.C., "The L-curve and its use in the numerical treatment of inverse problems", In: Johnston PR, Ed. Computational Inverse Problems in Electrocardiology. Southampton, UK: WIT Press; 2001:119-142.
[11] Golub, G.H., Heath, M., Wahba, G., "Generalized cross-validation as a method for choosing a good ridge parameter", Technometrics, 1979:21:215-223.
[12] Stein, C.M., "Estimation of the mean of a multivariate normal distribution", Ann Stat. 1981: 9: 1135-1151.
[13] Ramani, S., et al., "Regularization parameter selection for nonlinear iterative image restoration and MRI reconstruction using GCV and SURE-based methods", IEEE Transactions on Image Processing; 2012:21(8):3659-72.
[14] Guan, Y., et al., "Learn to better regularize in constrained reconstruction", in proceeding of International Society of Magnetic Resonance in Medicine (2021).
[15] Peng, X., et al., "Optimal regularization parameter selection for constrained reconstruction using deep learning", in proceeding of International Society of Magnetic Resonance in (2018).
[16] He J., Dong C., Qiao Y. "Modulating Image Restoration with Continual Levels via Adaptive Feature Modification Layers", In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2019:11056-- 11064.
[17] Kellman, P. and McVeigh, E.R., "Image Reconstruction in SNR Units: A General Method for SNR Measurement", Magn Reson Med. 2005; 54:1439-1447.

Figures

Figure1: The learned mapping between SNR and the regularization parameter. The proposed model was fitted (red) to the manually selected regularization parameters of training data collected with a variety of image contrasts, undersampling factors, and noise levels (black).

Figure 2: Example of patient data reconstructed using manual and automated regularization. The proposed auto-regularization approach produced similar image quality to that obtained through time-consuming manual tuning by four readers. Neuroradiologist reported no diagnostically significant difference between the two reconstructions. Even so, the auto-regularization approach clearly adapts to contrast-specific SNR conditions (note the decreased regularization in the T2* and T1w images).

Figure 3: Representative image slices of volunteer FLAIR data at acceleration factors R=2-4, demonstrating the ability of the proposed method to adapt to changes in acceleration factor. The GRAPPA reconstructions (provided for reference) and reconstructions using a fixed regularization parameter (tuned for R=2) demonstrate the increase in noise at higher acceleration factors. The automated regularization approach adapts to the increase in noise levels by increasing the regularization parameter. The regularization parameters are shown in upper left corner of each image.

Figure 4: Representative image slices of 2x undersampled FLAIR data acquired from a volunteer, demonstrating the ability of the proposed method to adapt to changes slice thickness. When the slice thickness is increased or decreased, the proposed method automatically adapts the regularization parameter (upper-left corner of each image) to account for the change in SNR, which results in more-consistent image quality as compared to reconstructions produced using a fixed regularization value.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

1052

DOI: https://doi.org/10.58530/2022/1052