Introduction:

Fast spin-echo sequence (FSE) is a popular sequence in clinical imaging because of its high sensitivity and high immunity against B₀ inhomogeneity artifacts. However, a prerequisite for its successful application is the fulfillment of the Carr-Purcell-Meiboom-Gill (CPMG) condition, which is often violated in diffusion-weighted magnetic resonance imaging due to the bulk motion. Existing solutions to this problem typically sacrifice half the signal intensity by eliminating interference between anti-CPMG components [1-3]. Diffusion-weighted half-Fourier acquisition single-shot turbo spin-echo (DW-HASTE) is a variant of the FSE method, which has found widespread applications in detecting small lesions. In this work, we describe DW-HASTE with the selective parity approach, first introduced in [4], and optimize the sequence for 3T in the context of multiple receive coil reception and parallel imaging.

Theory:

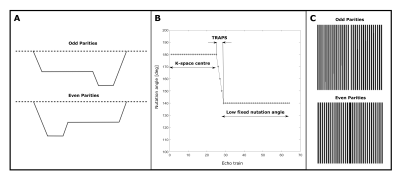
Acquisition: To avoid image artifacts caused by anti-CPMG components, the oldest and most commonly used approach is to acquire only one of the echo parities, while the other one is displaced out of the acquisition window, halving the sensitivity to the signal. To address this problem, displacing gradients were implemented, as described in [4], to preserve the full sensitivity of the method through benefiting from the contribution of both echo parities in the signal (figure 1A), by displacing the signal parity with the lowest contribution at each echo.
Shinnar Le-Roux (SLR) refocusing pulses were employed for their better slice profiles resulting in smooth echo amplitude decay over early echoes. This makes the use of dummy cycles for the echo amplitude stabilization unnecessary, which ultimately offers shorter echo time (TE) compared to the manufacturer’s method.
Smooth transition between pseudo steady states (TRAPS [5-6]) was employed to decrease the SAR contribution from the SLR pulses (figure 1B).
The original centre-out phase encoding scheme was also modified to sample the k-space with evenly distributed odd and even echo parities (figure 1C). This is advantageous to account for the effects of rotation, which will displace the k-space origin in opposite directions for odd and even parity echoes.
Reconstruction: Any bulk motion during the strong diffusion encoding gradients causes both phase shifts, due to translational motion, and phase gradients, due to rotational motion, in the image domain (reviewed in [7]). For SP-DW-HASTE data, this means that odd and even echo parities experience phase shifts and phase gradients of the same magnitude, but opposite polarity. As a result, in the frequency domain, both signals are shifted in the opposite directions in k-space. In addition, there is an arbitrary angle between the receiver and transmit phases for multi-channel receivers.
If it is chosen to split even and odd parity in an alternating fashion through the echo train, the image reconstruction algorithm should deal with the increased undersampling of k-space data (Figure 1C), which is twice the effective acceleration factor. Herein, SPIRIT [8] was used to provide an initial estimate of the missing data lines to generate separate odd and even parity images.
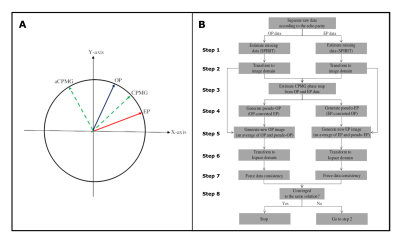
An iterative procedure was then used to ensure that odd and even parity images were complex conjugates of each other in the image domain (figure 2A). This iterative approach converges to a consistent representation of the non-acquired data lines without additional G-noise, and is depicted in figure 2B.
The critical step is the estimation of the CPMG phase map (step 3), which is subsequently used to convert odd parity to even parity data and vice versa (step 4). The information from both echo parities is then combined in step 5. After ~30 iterations (relative error below 1%), odd parity and even parity images eventually converge to the same solution, providing identical magnitude images.

Methods:

MRI in vivo scans were performed on a whole-body 3T Siemens Prisma scanner (80 mT/m strength and 200 mT/m/ms slew rate) with a 32-channel receive-only head coil in a healthy male volunteer. Data were collected with DW-HASTE and SP-DW-HASTE methods for b = 0 and 1000 s/mm². The common parameters were as follows: TR = 2000 ms, FOV = 200x200 mm², matrix size of 64*64, 3.1 mm isotropic in-plane resolution, 4 axial slices (3 mm), 20 repetitions, and acceleration factor 2 with 162s total scan time. A 3D diagonal diffusion weighting scheme was employed. Fat saturation was used for all acquisitions. TE was 89 ms for SP-DW-HASTE, and 112 ms for DW-HASTE. The frequency domain data were filtered with an exponential weighting function across phase encoding steps to approximate an exponential signal decay. A more sophisticated approach based on the calculated signal intensities could provide a further gain in SNR.

Results:

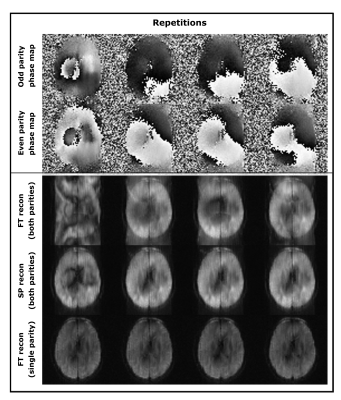
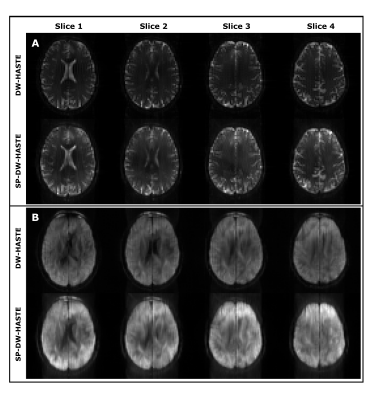
Figure 3 compares Fourier transform and selective parity reconstruction approaches. Example T₂-weighted and DW images obtained with DW-HASTE and SP-DW-HASTE methods are presented in figure 4.

Discussion:

Available methods for non-CPMG FSE imaging suffer mainly from low SNR and high SAR values, and their application is commonly limited to 1.5T. The presented approach addresses these problems by using both echo parities in the image formation, and applying variable flip angle refocusing pulses. To demonstrate the feasibility of the proposed approach, low resolution images are shown as a proof of principle. Further work will target higher acceleration factors, and improved efficiency to achieve improved spatial resolution.