1026
Bi-component dictionary for efficient quantification of fat fraction and water T1 via MR Fingerprinting1NMR Laboratory, Institute of Myology, Neuromuscular Investigation Center, Paris, France, 2NMR Laboratory, CEA, DRF, IBFJ, MIRCen, Paris, France
Synopsis
In the field of neuromuscular disorders (NMD), fat fraction (FF) is an established biomarker of disease severity and water T1 (T1H2O) has been shown to be a potential biomarker of disease activity. Those can be efficiently estimated through Magnetic Resonance Fingerprinting. However for muscle studies water-fat separation and FF quantification increase drastically the size of the dictionary and pattern matching time. We introduce here a bicomponent dictionary where water and fat signals are stored separately. This approach allows improving MRF performance and increasing the accuracy of FF quantification.
Introduction
In the field of neuromuscular disorders (NMD), fat fraction (FF) is an established biomarker of disease severity and water T1 (T1H2O) has been shown to be a potential biomarker of disease activity1. The use of MR Fingerprinting (MRF) enables the simultaneous quantification of various parameters2, such as FF and T1H2O. However, for muscle studies, water-fat separation and FF quantification increase drastically the size of the dictionary and pattern matching time (through the inclusion of FF as a dictionary parameter3,4) or require modification of the MRF sequence (through the inclusion of Dixon-like multi-echo patterns5). Furthermore, FF might be less accurately estimated - as it is discretized for minimizing the dictionary size.We introduce here a bicomponent dictionary (proposed method) where water and fat signals are stored separately for an adequate grid of T1H2O, B0 field inhomogeneity (Df), RF pulse attenuation (attB1) for the water signals and fat T1 (T1fat), Df, attB1 for the fat signals. In this work, we compared the accuracy, precision and performance of the parameters quantification using the proposed method, as compared to the single-component dictionary (reference method).
Methods
The sequence used for MRF is the T1-FF MRF presented in Marty et al.3, comprising a FLASH echo train with an initial inversion pulse, and variable TE, TR and FA. We use golden-angle radial sampling with a total of 1400 spokes. The spokes are grouped to form 175 undersampled images which are used for the fingerprinting.The bicomponent dictionary pattern matching algorithm uses direct dictionary matching, and a Principal Components Analysis (PCA) with 20 components on fat and water signals.
Under the bicomponent dictionary framework, the dimension of the pattern matching problem is reduced, as follows:
$$Argmin_{\mathbf{w}\in D_{w},\mathbf{f}\in D_{f},FF \in [0,1],\phi \in[-\pi,\pi]}||\frac{[(1-FF)*\mathbf{w}+FF*\mathbf{f}]}{||(1-FF)*\mathbf{w}+FF*\mathbf{f}||_{2}}e^{i\phi}-\mathbf{s}||_{2}^2$$
- s (resp. w, f) normalized pixel signal after reconstruction of 175 MRF images (resp. water signal, fat signal) in CT , T=175
- $$$\phi$$$ phase of the signal
- Nw , Nf number of water and fat dictionary entries
- Dw dictionary of water patterns (Nw x T)
- Df
dictionary of fat patterns (Nf
x T)
$$FF^*(w,f),\phi^*(w,f)=Argmin_{FF \in [0,1],\phi \in[-\pi,\pi]}||\frac{[(1-FF)*\mathbf{w}+FF*\mathbf{f}]}{||(1-FF)*\mathbf{w}+FF*\mathbf{f}||_{2}}e^{i\phi}-\mathbf{s}||_{2}^2$$
Step 2 : Traditional dictionary matching on remaining dictionary parameters
$$w^*,f^*=Argmin_{\mathbf{w}\in D_{w},\mathbf{f}\in D_{f}}||\frac{[(1-FF^*(w,f))*\mathbf{w}+FF^*(w,f)\mathbf{f}]}{||(1-FF^*(w,f))*\mathbf{w}+FF^*(w,f)*\mathbf{f}||_{2}}e^{i\phi^*(w,f)}-\mathbf{s}||_{2}^2$$
Solving step 1 is a straightforward resolution of equations with closed-form solutions, which can be efficiently vectorized :
$$\tan(\phi^*(w,f))=-\frac{FF^*(w,f)*Im(\Sigma_{fs})+(1-FF^*(w,f))*Im(\Sigma_{ws})}{FF^*(w,f)*Re(\Sigma_{fs})+(1-FF^*(w,f))*Re(\Sigma_{ws})} (1)$$
$$FF^*(w,f)=\frac{Re((\sigma_{fw}\Sigma_{ws}-v_{w}\Sigma_{fs})e^{i\phi^*(w,f)})}{Re(((\sigma_{fw}-v_{f})\Sigma_{ws}+(\sigma_{fw}-v_{w})\Sigma_{fs})e^{i\phi^*(w,f)})} (2)$$
Where :
$$\Sigma_{ws}=<\mathbf{w},\mathbf{s}>
\\\Sigma_{fs}=<\mathbf{f},\mathbf{s}>
\\\sigma_{fw}=Re(<\mathbf{f},\mathbf{w}>)
\\v_{w}=Re(<\mathbf{w},\mathbf{w}>)
\\v_{f}=Re(<\mathbf{f},\mathbf{f}>)$$
where $$$\\<\mathbf{s},\mathbf{d}>=\sum_{i=1}^T{s_i\bar{d_i}}$$$, calculated on the reduced timestep grid through principal components analysis (reduction of timesteps from 175 to 20 components).
Injecting the expression for $$$\tan(\phi^*(w,f))$$$ from (1) into (2) results in a closed-form formula for getting $$$FF^*(w,f)$$$ (2nd order polynomial equation).
We compared the implementation of our proposed method with the reference method implementation3, on numerical phantoms (5 square phantoms with randomly varying T1H2O, FF, Df and B1 in 90 square subregions, in the dictionary range described in Fig.1) and in vivo acquired data in legs and thighs for 21 healthy controls (129 imaged slices in total) and 49 NMD patients at various stages of the respective disease (149 imaged slices in total).
Through numeric phantoms, the goal was to compare the performance of the proposed method as well as FF quantification, as compared to the reference method. In vivo data were used to show that the results of the proposed method were comparable with the reference method. This was quantified by calculating R2 and bias on aggregated data for both numerical phantoms and patient data.
Results
On both phantoms and in vivo data, we can see increased accuracy and precision of the proposed method for the quantification of all parameters (Fig.2-3-4). Furthermore, the reference method systematically underestimates high FF and overestimates low FF (Fig.2-4). This leads to better contrast between low and high FF in the Invivo maps (Fig.5).The performance of the algorithm is improved due to dimension reduction and efficient vectorization. For the numeric square phantoms, the reference method takes 6min30s, whereas the proposed method takes 45s, and 6s when allowing for GPU. For invivo data, on an example subject with 9 imaged slices, the reference method finishes in 4h30min, compared with 2h50min for the proposed method, and 30min when allowing for GPU.
Discussion & Conclusion
The improvement of the quantification of FF is explained by the fact that FFs are not discretized. This leads to precision and accuracy improvement for the quantification of all parameters as the dimension reduction of the pattern searching problem reduces the probability of reaching local minima. A closed form formula was exposed in order to calculate the optimal FF in the bicomponent dictionary.The presented framework of bicomponent dictionary allows to accelerate the pattern matching of MRF in the muscle for rapid quantification of FF and T1H2O.
The results show that FF was systematically underestimated for high FF and overestimated for low FFs, using the reference method. The proposed method removes this bias, and, hence, increases the discriminatory power of the MRF maps between low and high fat fractions.
The reduced dictionary size paves the way for more granular dictionaries or additional parameters inclusion (e.g. diffusion, T2), which will allow to analyze and uncover potential biomarkers for NMD.
Acknowledgements
This study was funded by ANR-20-CE19-0004.References
[1] Marty, B., Reyngoudt, H., Boisserie, J. M., le Louër, J., Araujo, E. C. A., Fromes, Y., & Carlier, P. G. (2021). Water-fat separation in mr fingerprinting for quantitative monitoring of the skeletal muscle in neuromuscular disorders. Radiology, 300(3), 652–660. https://doi.org/10.1148/radiol.2021204028
[2] Ma, D., Gulani, V., Seiberlich, N., Liu, K., Sunshine, J. L., Duerk, J. L., & Griswold, M. A. (2013). Magnetic resonance fingerprinting. Nature, 495(7440), 187–192. https://doi.org/10.1038/nature11971
[3] Marty, B., & Carlier, P. G. (2020). MR fingerprinting for water T1 and fat fraction quantification in fat infiltrated skeletal muscles. Magnetic Resonance in Medicine, 83(2), 621–634. https://doi.org/10.1002/mrm.27960
[4] Cencini, M., Biagi, L., Kaggie, J. D., Schulte, R. F., Tosetti, M., & Buonincontri, G. (2019). Magnetic resonance fingerprinting with dictionary-based fat and water separation (DBFW MRF): A multi-component approach. Magnetic Resonance in Medicine, 81(5), 3032–3045. https://doi.org/10.1002/mrm.27628
[5] Koolstra, K., Webb, A. G., Veeger, T. T. J., Kan, H. E., Koken, P., & Börnert, P. (2020). Water–fat separation in spiral magnetic resonance fingerprinting for high temporal resolution tissue relaxation time quantification in muscle. Magnetic Resonance in Medicine, 84(2), 646–662. https://doi.org/10.1002/mrm.28143
Figures
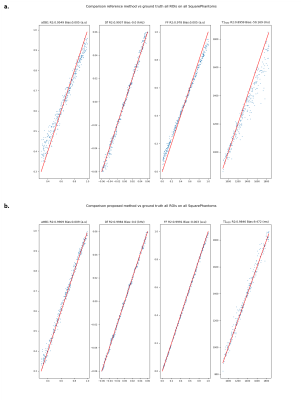
Fig.2: Comparison of retrieved parameters on 5 square phantoms between reference method and proposed method vs ground truth on all ROIs. a. Regression of attB1, Df, FF, T1H2O of reference method vs ground truth. b. Regression of attB1, Df, FF, T1H2O of proposed method vs ground truth
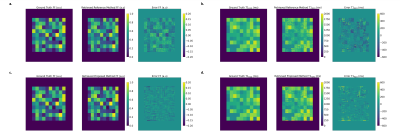
Fig.3: FF and T1H2O map reference method and proposed method vs ground truth on one example numeric square phantom. a. FF map ground truth, reference method and error. We can see the quantification error leading to a checkerboard error pattern. b. T1H2O map ground truth, reference method and error. c. FF map ground truth, proposed method and error. d. T1H2O map ground truth, proposed method and error
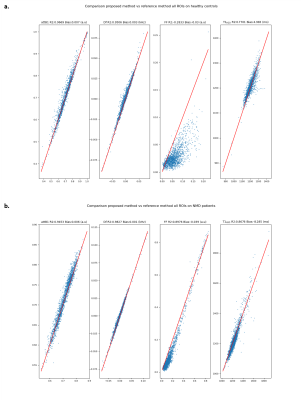
Fig.4: Comparison of retrieved parameters between reference method and proposed method vs ground truth on all ROIs for healthy controls and NMD patients in legs and thighs. a. Regression of attB1, Df, FF, T1H2O of proposed method vs reference method for healthy controls. b. Regression of attB1, Df, FF, T1H2O of proposed method vs reference method for NMD patients
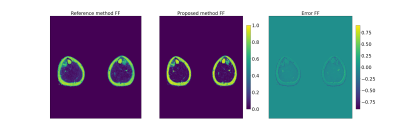
Fig.5: FF map comparison in the legs for a patient with a distal myopathy. From left to right : FF maps reference method, proposed method and difference