1010
Performance of Quantitative, Free-breathing 3D Perfusion CMR using Motion-Informed LLR Reconstruction in a Porcine Infarction Model1Institute for Biomedical Engineering, University and ETH Zurich, Zurich, Switzerland, 2Center of Surgical Research, University Hospital Zurich, University of Zurich, Zurich, Switzerland, 3Department of Health Sciences and Technology, ETH Zurich, Zurich, Switzerland
Synopsis
Three-dimensional first-pass myocardial perfusion CMR requires acceleration methods to enable whole-heart coverage in a limited acquisition window. Current 3D approaches suffer from data inconsistencies during free breathing, compromising image quality and perfusion quantification. We propose and experimentally validate a combination of Cartesian pseudo-spiral k-t undersampling with respiratory motion-informed locally low-rank (MI-LLR) reconstruction for robust whole-heart myocardial quantitative perfusion CMR in an experimental pig model of myocardial infarction. As reference, standard 2D acquisitions are used. Overall, image quality scoring was good. Perfusion defects were equally well depicted and discernible in imaging and MBF perfusion mapping in 3D and 2D approaches, respectively.
Introduction
Three-dimensional first-pass myocardial perfusion CMR requires acceleration methods to enable whole-heart coverage in the limited acquisition window available in each cardiac cycle1. Current 3D approaches suffer from data inconsistencies during free breathing, compromising image quality and perfusion quantification. Cartesian pseudo-spiral k-t undersampling schemes with respiratory motion-informed locally low-rank reconstruction (MI-LLR)2 hold promise to address current shortcomings. By utilizing data correlations based on patch-based decomposition of the multi-dimensional data frames3, robust free-breathing whole-heart myocardial quantitative perfusion CMR becomes possible.For the successful translation into clinical practice, the performance of MI-LLR has to be assessed relative to current clinical 2D protocols. In addition, the sensitivity and robustness of MI-LLR as a function of regularization strength and patch size remain to be studied in detail with respect to qualitative and quantitative differences.
The present study aims at providing performance indicators of free-breathing 3D MI-LLR relative to standard 2D acquisitions using an experimental porcine model of myocardial infarction in which, in contrast to patients, repeat acquisitions are permitted. Image quality and perfusion maps of MI-LLR, depending on patch size, were assessed by five radiologists and compared to 2D data.
Methods
FPP data were acquired during free-breathing in five female pigs (Swiss large white, 80-85 kg) after induction of myocardial infarction using 90-min occlusion of coronary arteries and/or injection of endogenous micro-thrombi, administered directly in one coronary artery. 3D and 2D perfusion protocols were performed in succession i.e. 3D MI-LLR was followed by standard 2D-SENSE with a pause of 2 min in-between. Contrast dosage was$$$\,\,0.075\,mmol/kg\,b.w.\,\,$$$(3D) and$$$\,\,0.1\,mmol/kg\,b.w.\,\,$$$(2D) and injection speed was$$$\,\,4\,ml/s\,\,$$$(Gadovist, Bayer Schering Pharma, Germany). All animal handling, procedures and protocols were approved by the Cantonal Veterinary Office (Zurich, Switzerland).A dynamically interleaved 2D/3D dual-sequence, single-bolus scheme based on an electrocardiogram (ECG) triggered, saturation-recovery4, spoiled gradient-echo sequence was used as described previously5. The pseudo-spiral Cartesian undersampling pattern was implemented as illustrated in$$$\,\,Figure\,1A$$$2. Imaging parameters were:$$$\,\,TR/TE\,=\,2.0/1.0\,ms,\,\,$$$spatial resolution:$$$\,\,2.5\,x\,2.5\,x\,10\,mm^3,\,\,$$$flip angle:$$$\,\,15°,\,\,$$$acquisition window:$$$\,\,240\,ms,\,\,$$$saturation delay:$$$\,\,135\,ms,\,$$$undersampling factor$$$\,R\,=10.$$$
For the interleaved acquisition of the arterial input function (AIF), a centre-out Cartesian pattern with: spatial resolution:$$$\,10\,x\,10\,mm^2,\,\,$$$slice thickness:$$$\,\,15\,mm,\,\,$$$flip angle:$$$\,\,15°,\,\,$$$acquisition window:$$$\,\,56-64\,ms,\,\,$$$saturation delay:$$$\,\,30\,ms$$$.
As reference, a 2D perfusion dual-sequence scheme was implemented to interleave a 2D AIF measurement with a clinical three-slice 2D protocol. Parameters were:$$$\,\,TR/TE\,=\,2.5/1.2\,ms,\,\,$$$spatial resolution:$$$\,\,2.5\,x\,2.5\,x\,10\,mm^3,\,\,FOV:\,\,320\,x\,320\,mm^2,\,\,$$$three slices, flip angle:$$$\,\,20°,\,\,$$$acquisition window per slice:$$$\,\,141\,\,ms,\,\,$$$saturation delay:$$$\,\,100\,\,ms,\,\,$$$undersampling factor$$$\,\,R\,=2.3\,\,$$$(SENSE). AIF parameters were identical to the 3D/2D scheme. All images were acquired on a$$$\,\,1.5\,T\,\,$$$Philips MR system (Philips Healthcare, Best, The Netherlands) using a 5-element cardiac receive coil array.
Given the zero-filled k-space data$$$\,\,\bf{s}\in \mathbb{C}^{N_{s}N_{c}\times T}\,\,$$$with$$$\,\,T\,\,$$$dynamics,$$$\,\,N_c\,\,$$$coils, containing$$$\,\,N_s\,\,$$$k-space samples, the MI-LLR reconstruction$$$\,\,\bf{I}_{MI-LLR}\in \mathbb{C}^{N_{v}\times T}\,\,$$$of$$$\,\,N_v\,\,$$$voxels is achieved by solving the convex optimization problem3 using a proximal gradient descent method6:$$\bf{I}_{MI-LLR}=\arg\min_{\bf{I}}||\bf{\Omega}\mathcal{\bf{\it{F}}}\bf{C}[\mathcal{\bf{Q_1}}\bf{i}_1,...,\mathcal{\bf{Q_T}}\bf{i}_T]-\bf{s}||_2^2+\lambda_{MI-LLR}\sum_{\it{b}\in\it{U}}||\bf{P}_{\it{b}}\bf{I}||_*,$$with undersampling operator$$$\,\,\bf{\Omega},\,\,$$$Fourier transform$$$\,\,\mathcal{\bf{\it{F}}},\,\,$$$coil sensitivities:$$$\,\,\bf{C}\,\,$$$and regularization weight$$$\,\,\lambda_{MI-LLR}.\,\,$$$The patch operator$$$\,\,\bf{P}_{b}\in \left\{0,1\right\}^{n_{x}n_{y}n_{z}\times N_{v}}\,\,$$$refers to the b-th patch, where$$$\,\,\bf{U}\,\,$$$is a set of patch indices, with patch size of$$$\,\,\bf{n}=\,n_x\,x\,n_y\,x\,n_z\,\,$$$voxels.$$$\,\,\bf{Q_T}\,\,$$$denotes the inverted displacement field from initial reconstruction2,7. The minimum value of the regularization parameter$$$\,\,\lambda_{MI-LLR},\,\,$$$which suppresses background signal variation to$$$\,\,0.05\,%\,\,$$$of the maximum image intensity, was chosen.
2D data were reconstructed on the scanner using the product SENSE implementation.
Post-processing and perfusion quantification were conducted in MATLAB. The 2D perfusion data was registered prior quantification7. Myocardial blood flow (MBF) quantification was performed using Fermi model deconvolution9.
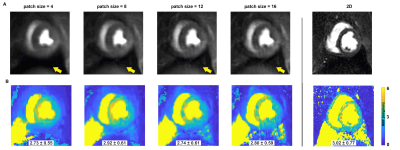
The 3D MI-LLR perfusion data were reconstructed with four different patch sizes$$$\,\,\bf{n}\,\,$$$(i.e. 4, 8, 12, 16). Five radiologists scored the image quality of the blinded and randomized data according to a Likert scale (from 1-5) as detailed in$$$\,\,Figure\,2A.$$$
Results
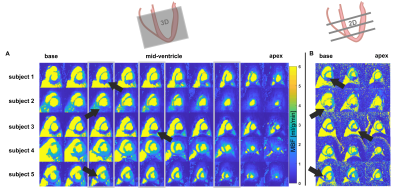
Image quality scoring$$$\,\,(Figure\,2)\,\,$$$indicates acceptable to good image quality overall. For patch sizes≤8, minimum scoring was acceptable, whereas larger patch sizes≥12, were scored as diagnostically insufficient in 14% of ratings.Perfusion deficits are well resolved in dynamic image series and in perfusion maps$$$\,\,(Figure\,3-4).\,\,$$$Exemplary image quality and quantification results for varying patch sizes are shown in$$$\,\,Figure\,5,\,\,$$$with corresponding c-t curves shown in$$$\,\,Figure\,1C-D.\,\,$$$Spatial resolution is noticeably decreased from higher to lower patch sizes (right to left). Inversely, streaking artefacts are reduced.
Discussion
Resulting 3D image series and MBF mapping compare well to subsequently acquired 2D perfusion datasets. Regional deviations at the basal level are associated with inflow artefacts. Comparable detection of myocardial infarction in image series and MBF mapping, despite the 5x higher undersampling factor, was accomplished and compares well to previous 3D studies with data acquisition in breath-hold5,9. The 2D reference data was registered during post-processing, and might therefore suffer from residual motion artefacts. For better reference, especially in humans, acquisitions during breath-hold might be more reliable10. As no time for contrast washout between 3D and 2D was allowed, appearance is ill-balanced and quantification of the 2D data is prone to uncertainties, e.g. invoked by saturation of AIF signal.Rating per expert reflects that reviewers prefer different flavors of reconstruction. Rating per dataset reflects that patch size preference cannot be generalized to all datasets.
Next steps entail detailed comparison of MBF values in 3D and 2D. Statistical evaluation of MBF in infarct and remote tissue is of special interest. Future scoring should cover 3D, as well as 2D imaging and corresponding MBF maps.
Conclusion
Free-breathing 3D MI-LLR provides diagnostic image quality and perfusion metrics, capable of detecting local perfusion deficits with comparable accuracy to standard 2D perfusion imaging with the added benefit of whole-heart coverage as demonstrated in this preliminary study of experimental cardiac infarction.Acknowledgements
The authors acknowledge research support of Innosuisse, grant: 31010.1 IP-LSReferences
1. Fair MJ, Gatehouse PD, DiBella EVR, Firmin DN. A review of 3D first-pass, whole-heart, myocardial perfusion cardiovascular magnetic resonance. J. Cardiovasc. Magn. Reson. 2015;17:1–25 doi: 10.1186/s12968-015-0162-9.
2. Hoh T, Vishnevskiy V, Fuetterer M, Kozerke S. Free-Breathing Motion-Informed Quantitative 3D Myocardial Perfusion Imaging. In: Proc. Int. Symp. Magn. Reson. Med. ; 2021. p. 4371.
3. Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn. Reson. Med. 2015;73:655–661 doi: 10.1002/mrm.25161.
4. Ogg RJ, Kingsley PB, Taylor JS. WET, a T1- and B1-Insensitive Water-Suppression Method for in Vivo Localized1H NMR Spectroscopy. J. Magn. Reson. Ser. B 1994;104:1–10 doi: 10.1006/jmrb.1994.1048.
5. Wissmann L, Niemann M, Gotschy A, Manka R, Kozerke S. Quantitative three-dimensional myocardial perfusion cardiovascular magnetic resonance with accurate two-dimensional arterial input function assessment. J. Cardiovasc. Magn. Reson. 2015;17:1–11 doi: 10.1186/s12968-015-0212-3.
6. Beck A, Teboulle M. A Fast Iterative Shrinkage-Thresholding Algorithm. Soc. Ind. Appl. Math. J. Imaging Sci. 2009;2:183–202.
7. Vishnevskiy V, Gass T, Szekely G, Tanner C, Goksel O. Isotropic Total Variation Regularization of Displacements in Parametric Image Registration. IEEE Trans. Med. Imaging 2017;36:385–395 doi: 10.1109/TMI.2016.2610583.
8. Jerosch-herold M, Wilke N, Stillman AE, et al. Magnetic resonance quantification of the myocardial perfusion reserve with a Fermi function model for constrained deconvolution Magnetic resonance quantification of the myocardial perfusion reserve with a Fermi function model for constrained deconvolution. Med. Physiol. 1998;25:73–84 doi: 10.1118/1.598163.
9. Manka R, Wissmann L, Gebker R, et al. Multicenter Evaluation of Dynamic Three-Dimensional Magnetic Resonance Myocardial Perfusion Imaging for the Detection of Coronary Artery Disease Defined by Fractional Flow Reserve. Circ. Cardiovasc. Imaging 2015;8:1–7 doi: 10.1161/CIRCIMAGING.114.003061.
10. Schmidt JFM, Wissmann L, Manka R, Kozerke S. Iterative k-t principal component analysis with nonrigid motion correction for dynamic three-dimensional cardiac perfusion imaging. Magn. Reson. Med. 2014;72:68–79 doi: 10.1002/mrm.24894.
Figures

Figure 1: Outline of Cartesian pseudo-spiral k-t undersampling with respiratory motion-informed locally low-rank reconstruction (MI-LLR). A) Undersampling density function and Cartesian spiral-in – spiral-out pattern in the kz-/ky-domain for a single time frame. B) MI-LLR reconstruction using patches P. Using the deformation field derived from an initial LLR reconstruction, image time series are reconstructed. C) Following segmentation, concentration time (c-t) curves are derived. D) Varying sizes of the patches influence contrast dynamics as indicated by the c-t curves.
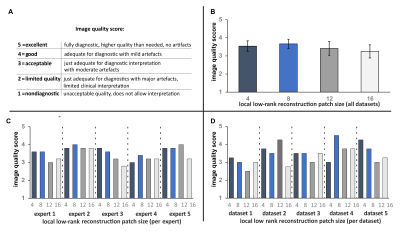
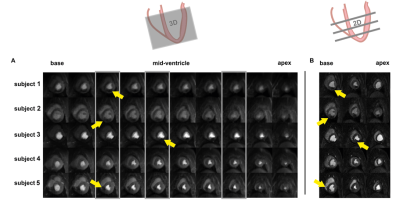
Figure 3: Dynamic comparison of image quality of 3D (A) versus 2D (B) perfusion imaging. Locations of the acquired 2D slices are indicated by grey boxes in (A). Example locations of infarctions are highlighted by yellow arrows.