1005
Free-running 3D T1 and T2 myocardial mapping and cine MRI in 3 mins using low-rank non-rigid motion-corrected reconstruction
Andrew Phair1, Gastao Cruz1, Haikun Qi2, René Botnar1, and Claudia Prieto1
1School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 2School of Biomedical Engineering, Shanghai Tech University, Shanghai, China
1School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 2School of Biomedical Engineering, Shanghai Tech University, Shanghai, China
Synopsis
Recent work has enabled the simultaneous acquisition of 3D myocardial T1 and T2 maps with isotropic spatial resolution and cardiac cine images from a ~10-minute scan. Herein, we propose to incorporate non-rigid cardiac motion correction into a dictionary-based low-rank reconstruction scheme, allowing k-space data from all cardiac phases to be included in the reconstruction of any given phase. Reconstructed cine images and T1 and T2 maps with and without motion correction are presented and demonstrate that a reduction to 30% of the acquired k-space data (~3-minute scan) can be achieved while image quality is maintained.
Introduction
The free-running simultaneous acquisition of 3D myocardial $$$T_1$$$ and $$$T_2$$$ maps with isotropic spatial resolution and cardiac cine images has recently been achieved with a ~10-minute scan using a 3D golden-angle radial trajectory and rigid-respiratory-motion correction1,2. In that study, k-space spokes were ECG-gated to cardiac phases, and hence only a fraction of the acquired data was used in the reconstruction of each phase. Here, we propose to incorporate non-rigid cardiac motion correction3 into the reconstruction framework, allowing all acquired data to be used at each phase and thus enabling the simultaneous acquisition of 3D whole-heart $$$T_1$$$ and $$$T_2$$$ maps and cine images in ~3 minutes.Methods
Data were acquired using a low flip angle spoiled gradient echo readout with a 3D golden-angle radial trajectory2. Sufficient $$$T_1$$$ and $$$T_2$$$ encoding was achieved by repeating the three-shot cycle in Figure 1(a); each shot was preceded by an IR pulse alongside (for two of the shots) a $$$T_2$$$-prep pulse with an echo time of 30 ms or 60 ms.Respiratory binning was performed using a respiratory signal extracted from the centre of k-space1, with auxiliary bin images used to estimate and correct the k-space data for 3D rigid respiratory motion.
The respiratory-motion-corrected k-space spokes were sorted into $$$Q$$$ cardiac phases ($$$Q=10$$$ for $$$T_1$$$/$$$T_2$$$ maps, $$$Q=16$$$ for cine images) and for each phase a soft-weighted4 GROG5 reconstruction was implemented. Non-rigid 3D motion fields were estimated between each phase and a reference phase ($$$T_1$$$/$$$T_2$$$ maps) or between every pair of phases (cine) using a free-form deformation algorithm6.
A dictionary of signal evolutions over the three-shot cycle for different $$$(T_1,T_2)$$$ combinations was simulated and then compressed by retaining only the highest singular values from an SVD decomposition of the dictionary matrix7.
The reconstruction of multi-singular-contrast 3D images followed the low-rank motion-corrected (LRMC) approach of Cruz et al.3 by integrating non-rigid cardiac motion correction with the previous dictionary-based low-rank inversion (LRI)7 reconstruction and low-rank patch-based HD-PROST8 denoising, and thus proceeded by minimising
$$\mathcal{L}\left(\boldsymbol{\rho},\mathcal{T},\mathbf{Y}\right)=\|E\boldsymbol{\rho}-W\mathbf{k}\|_2^2+λ\sum_p\|\mathcal{T}_p\|_*+\frac{\mu}{2}\|\mathcal{T}_p-P_p(\boldsymbol{\rho})-P_p\left(\mathbf{Y}\right)\|_F^2$$
via an ADMM iteration scheme9. Here, for $$$N$$$ voxels, $$$N_c$$$ coils, $$$r$$$ singular contrasts, $$$K$$$ total k-space samples and $$$K_q$$$ k-space samples at the $$$q$$$th cardiac phase, $$$\boldsymbol{\rho}\in\mathbb{C}^{Nr\times\,1}$$$ is the multi-singular-contrast 3D image vector we are solving for; $$$\mathbf{k}\in\mathbb{C}^{KN_c\times\,1}$$$ is the vector of rigid-motion-corrected multi-coil k-space data; $$$W\in\mathbb{R}^{KN_c\times\,KN_c}$$$ contains radial-sampling-density-compensation weights; $$$\mathcal{T}_p$$$ is the HD-PROST tensor of patches similar to the patch centred at the $$$p$$$th voxel; $$$P_p$$$ is a patch-selection operator; $$$\mathbf{Y}$$$ is the augmented Lagrangian; $$$\lambda$$$ and $$$\mu$$$ are penalty weightings; $$$\ast$$$ and $$$F$$$ denote the nuclear and Frobenius norms, respectively; and $$$E=\sum_{q}WU_rA_qF_qSM_q$$$ is the encoding operator, which consists of $$$M_q\in\mathbb{R}^{Nr\times\,Nr}$$$, which applies the motion distortion for the $$$q$$$th cardiac phase, $$$S\in\mathbb{C}^{NN_cr\times\,Nr}$$$, the estimated coil sensitivity maps, $$$F_q\in\mathbb{C}^{K_qN_cr\times\,NN_cr}$$$, the non-uniform Fourier operator that transforms the 3D multi-coil multi-singular-contrast image to a corresponding 3D radial k-space with only those spokes acquired at the $$$q$$$th cardiac phase, $$$A_q\in\mathbb{N}^{KN_cr\times\,K_qN_cr}$$$, which positions $$$q$$$th-phase spokes into the full radial trajectory, and $$$U_r\in\mathbb{R}^{KN_c\times\,KN_cr}$$$, which contains the dictionary compression weights that relate the singular contrasts to the $$$T_1$$$- and $$$T_2$$$-weighting of the contrast that each spoke was acquired with.
To obtain cine images, the process was repeated with each cardiac phase set as the reference. To obtain 3D $$$T_1$$$ and $$$T_2$$$ maps, the multi-singular-contrast images were compared voxel-wise with the entries of the compressed dictionary. The $$$T_1$$$ and $$$T_2$$$ values used in the generation of the dictionary entry with the closest fit (determined by a dot product of normalised vectors) were assigned to that voxel in the maps.
For comparison, LRI (motion-resolved) reconstructions2 ($$$M=I$$$) were also implemented. In this case, $$$\mathbf{k}\in\mathbb{C}^{K_qN_c\times\,1}$$$ contained only the rigid-motion-corrected k-space data acquired at the $$$q$$$th cardiac phase.
Results
Singular-contrast images and parameter maps for a healthy subject, obtained using LRMC and LRI reconstruction with varying amounts of k-space data, are presented in Figure 2 without regularisation ($$$\lambda=\mu=0$$$) to best demonstrate the improvement from non-rigid motion correction. $$$T_1$$$ and $$$T_2$$$ maps obtained with the proposed approach (30% of data, LRMC, HD-PROST) are shown in Figure 3 alongside conventional 2D mapping techniques (MOLLI and GraSE) for two subjects. AHA bullseye plots10 are presented in Figure 4 for one subject, alongside boxplots of the means and standard deviations of the mean recorded in each segment across 11 subjects for LRMC and LRI reconstructions and 100% or 30% of the acquired data. A cine of the 2nd singular-contrast image using the proposed approach, shown for nine short-axis slices, is presented in Figure 5.Discussion
Results suggest that similar levels of accuracy and precision can be attained using only 30% of the acquired data when cardiac motion correction is incorporated. The proposed approach is seen to produce 3D maps of comparable quality to the conventional 2D mapping sequences and prevents the large increase in the standard deviation of myocardial $$$T_1$$$ and $$$T_2$$$ values seen in the motion-resolved reconstruction when using 30% of data.Conclusion
By incorporating motion correction into the previous free-running simultaneous 3D myocardial $$$T_1$$$ and $$$T_2$$$ mapping and cine imaging framework, similar image quality was achieved with only 30% of the acquired k-space data, corresponding to a scan time reduction from ~10 minutes to ~3 minutes.Acknowledgements
This work was supported by EPSRC (EP/P001009, EP/P032311/1, EP/P007619/1) and Wellcome EPSRC Centre for Medical Engineering (NS/ A000049/1).References
1. Qi, H., Jaubert, O., Bustin, A., Cruz, G., Chen, H., Botnar, R., & Prieto, C. (2019). Free‐running 3D whole heart myocardial T1 mapping with isotropic spatial resolution. Magnetic resonance in medicine, 82(4), 1331-1342.2. Qi, H., Bustin, A., Cruz, G., Jaubert, O., Chen, H., Botnar, R. M., & Prieto, C. (2019). Free-running simultaneous myocardial T1/T2 mapping and cine imaging with 3D whole-heart coverage and isotropic spatial resolution. Magnetic resonance imaging, 63, 159-169.
3. Cruz, G., Qi, H., Jaubert, O., Kuestner, T., Schneider, T., Botnar, R. M., & Prieto, C. (2021). Generalized low‐rank nonrigid motion‐corrected reconstruction for MR fingerprinting. Magnetic Resonance in Medicine.
4. Küstner, T., Bustin, A., Jaubert, O., Hajhosseiny, R., Masci, P. G., Neji, R., Botnar, R. & Prieto, C. (2021). Fully self‐gated free‐running 3D Cartesian cardiac CINE with isotropic whole‐heart coverage in less than 2 min. NMR in Biomedicine, 34(1), e4409.
5. Seiberlich, N., Breuer, F. A., Blaimer, M., Barkauskas, K., Jakob, P. M., & Griswold, M. A. (2007). Non‐Cartesian data reconstruction using GRAPPA operator gridding (GROG). Magnetic Resonance in Medicine, 58(6), 1257-1265.
6. Modat, M., Ridgway, G. R., Taylor, Z. A., Lehmann, M., Barnes, J., Hawkes, D. J., Fox, N. C. & Ourselin, S. (2010). Fast free-form deformation using graphics processing units. Computer methods and programs in biomedicine, 98(3), 278-284.
7. Assländer, J., Cloos, M. A., Knoll, F., Sodickson, D. K., Hennig, J., & Lattanzi, R. (2018). Low rank alternating direction method of multipliers reconstruction for MR fingerprinting. Magnetic resonance in medicine, 79(1), 83-96.
8. Bustin, A., Lima da Cruz, G., Jaubert, O., Lopez, K., Botnar, R. M., & Prieto, C. (2019). High‐dimensionality undersampled patch‐based reconstruction (HD‐PROST) for accelerated multi‐contrast MRI. Magnetic resonance in medicine, 81(6), 3705-3719.
9. Boyd, S., Parikh, N., & Chu, E. (2011). Distributed optimization and statistical learning via the alternating direction method of multipliers. Now Publishers Inc.
10. American Heart Association Writing Group on Myocardial Segmentation and Registration for Cardiac Imaging:, Cerqueira, M. D., Weissman, N. J., Dilsizian, V., Jacobs, A. K., Kaul, S., Laskey, W. K., Pennell, D. J., Rumberger, J. A., Ryan, T., & Verani, M. S. (2002). Standardized myocardial segmentation and nomenclature for tomographic imaging of the heart: a statement for healthcare professionals from the Cardiac Imaging Committee of the Council on Clinical Cardiology of the American Heart Association. Circulation, 105(4), 539-542.
Figures
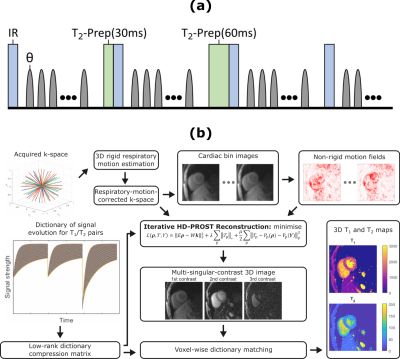
Fig 1. (a) Diagram of the 3D golden-angle radial
acquisition sequence. Sequence parameters included: flip angle $$$\theta=6^\circ$$$, TR = 10.3 ms, TE = 4.6 ms, FOV = 200 mm$$$\times$$$200
mm$$$\times$$$200 mm,
spatial resolution = 2 mm$$$\times$$$2 mm$$$\times$$$2 mm, no.
of readouts = 195. (b)
Schematic of the reconstruction framework.
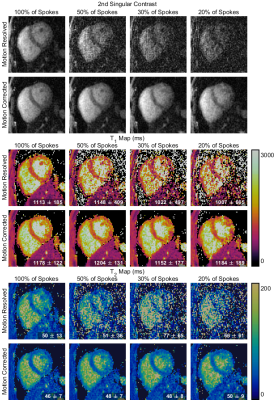
Fig 2. Mid-short-axis slice of 3D singular contrast images and $$$T_1$$$ and $$$T_2$$$ maps obtained with LRI (top row) and LRMC (bottom row) reconstruction and different amounts of the total acquired k-space data. The mean and standard deviation of the parameter values in the septum region is given in the corner for each $$$T_1$$$ and $$$T_2$$$ map.

Fig 3. Comparison of $$$T_1$$$ and $$$T_2$$$ maps for two subjects acquired using the established 2D mapping sequences MOLLI ($$$T_1$$$) and GraSE ($$$T_2$$$) and the proposed 3D LRMC approach with 30% of the acquired data and HD-PROST regularisation. The MOLLI and GraSE maps are shown for a mid-short-axis slice, whereas for the proposed sequence three short-axis slices (apex, mid and base) are displayed, alongside a vertical-long-axis slice.
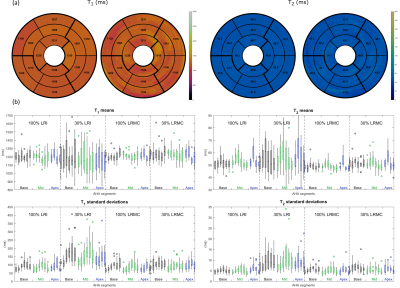
Fig 4. (a) AHA bullseye plots for one subject using the LRMC approach with 30% of acquired data. High-resolution plots (right) show myocardial values over many slices, these are averaged over the apex, mid and base in the low-resolution plots (left). (b) Boxplots of the mean (top) and standard deviation (bottom) of the mean values in each bullseye segment across 11 subjects using 100% or 30% of acquired data, and either a motion-resolved (LRI) or motion-corrected (LRMC) reconstruction.
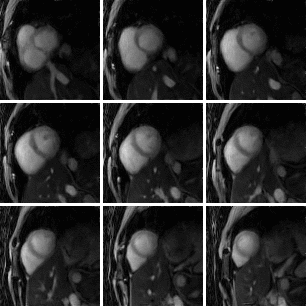
Fig 5. Example 16-phase 3D cine image using 30% of the acquired k-space data. Nine short axis slices are shown, from base (top left) to apex (bottom right).
DOI: https://doi.org/10.58530/2022/1005